Learning Visual-Semantic Subspace Representations for Propositional Reasoning

Learning representations that capture rich semantic relationships and accommodate propositional calculus poses a significant challenge. Existing approaches are either contrastive, lacking theoretical guarantees, or fall short in effectively representing the partial orders inherent to rich visual-semantic hierarchies. In this paper, we propose a novel approach for learning visual representations that not only conform to a specified semantic structure but also facilitate probabilistic propositional reasoning. Our approach is based on a new nuclear norm-based loss. We show that its minimum encodes the spectral geometry of the semantics in a subspace lattice, where logical propositions can be represented by projection operators.

2D Image head pose estimation via latent space regression under occlusion settings

Head orientation is a challenging Computer Vision problem that has been extensively researched having a wide variety of applications. However, current state-of-the-art systems still underperform in the presence of occlusions and are unreliable for many task applications in such scenarios. This work proposes a novel deep learning approach for the problem of head pose estimation under occlusions. The strategy is based on latent space regression as a fundamental key to better structure the problem for occluded scenarios. Our model surpasses several state-of-the-art methodologies for occluded HPE, and achieves similar accuracy for non-occluded scenarios. We demonstrate the usefulness of the proposed approach with: (i) two synthetically occluded versions of the BIWI and AFLW2000 datasets, (ii) real-life occlusions of the Pandora dataset, and (iii) a real-life application to human-robot interaction scenarios where face occlusions often occur. Specifically, the autonomous feeding from a robotic arm.

Hyperbolic vs Euclidean Embeddings in Few-Shot Learning: Two Sides of the Same Coin

Recent research in representation learning has shown that hierarchical data lends itself to low-dimensional and highly informative representations in hyperbolic space. However, even if hyperbolic embeddings have gathered attention in image recognition, their optimization is prone to numerical hurdles. Further, it remains unclear which applications stand to benefit the most from the implicit bias imposed by hyperbolicity, when compared to traditional Euclidean features. In this paper, we focus on prototypical hyperbolic neural networks. In particular, the tendency of hyperbolic embeddings to converge to the boundary of the Poincar\'e ball in high dimensions and the effect this has on few-shot classification. We show that the best few-shot results are attained for hyperbolic embeddings at a common hyperbolic radius. In contrast to prior benchmark results, we demonstrate that better performance can be achieved by a fixed-radius encoder equipped with the Euclidean metric, regardless of the embedding dimension.

Rotation Averaging in a Split Second: A Primal-Dual Method and a Closed-Form for Cycle Graphs

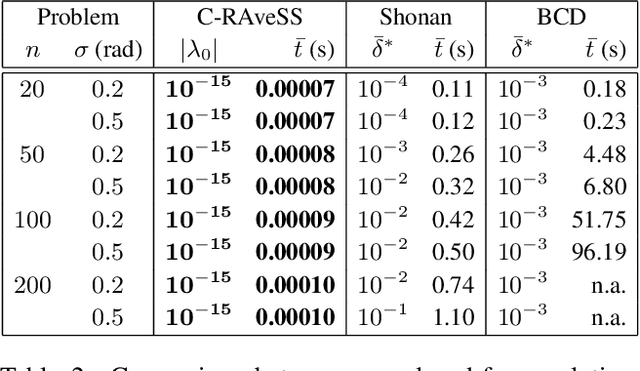
A cornerstone of geometric reconstruction, rotation averaging seeks the set of absolute rotations that optimally explains a set of measured relative orientations between them. In spite of being an integral part of bundle adjustment and structure-from-motion, averaging rotations is both a non-convex and high-dimensional optimization problem. In this paper, we address it from a maximum likelihood estimation standpoint and make a twofold contribution. Firstly, we set forth a novel initialization-free primal-dual method which we show empirically to converge to the global optimum. Further, we derive what is to our knowledge, the first optimal closed-form solution for rotation averaging in cycle graphs and contextualize this result within spectral graph theory. Our proposed methods achieve a significant gain both in precision and performance.

LocDyn: Robust Distributed Localization for Mobile Underwater Networks

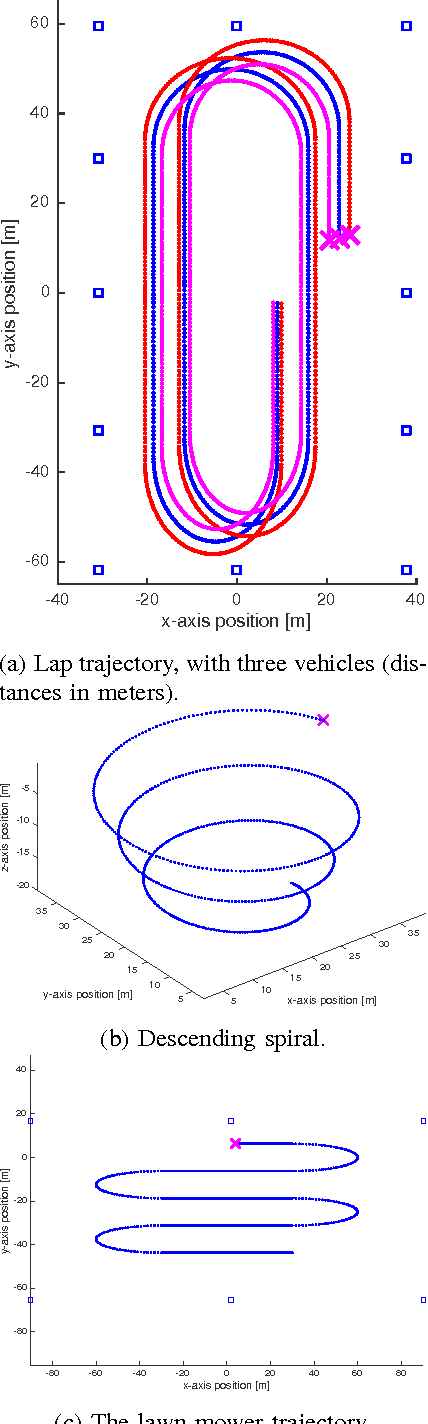
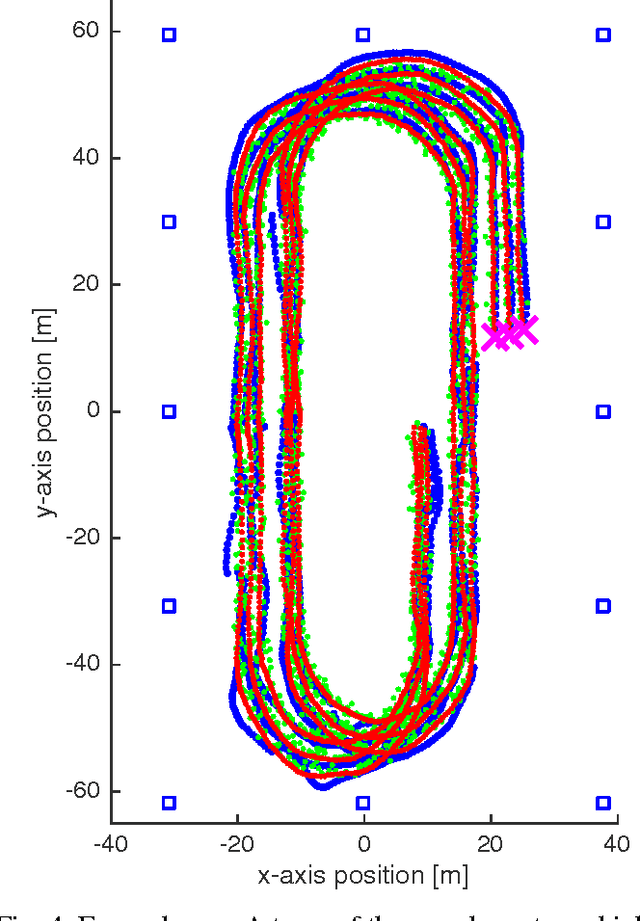
How to self-localize large teams of underwater nodes using only noisy range measurements? How to do it in a distributed way, and incorporating dynamics into the problem? How to reject outliers and produce trustworthy position estimates? The stringent acoustic communication channel and the accuracy needs of our geophysical survey application demand faster and more accurate localization methods. We approach dynamic localization as a MAP estimation problem where the prior encodes dynamics, and we devise a convex relaxation method that takes advantage of previous estimates at each measurement acquisition step; The algorithm converges at an optimal rate for first order methods. LocDyn is distributed: there is no fusion center responsible for processing acquired data and the same simple computations are performed for each node. LocDyn is accurate: experiments attest to a smaller positioning error than a comparable Kalman filter. LocDyn is robust: it rejects outlier noise, while the comparing methods succumb in terms of positioning error.