Hyperbolic vs Euclidean Embeddings in Few-Shot Learning: Two Sides of the Same Coin
Paper and Code
Sep 18, 2023
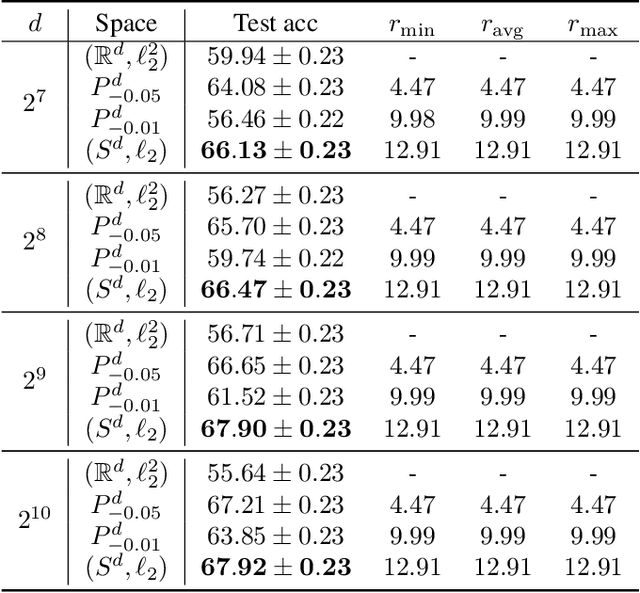

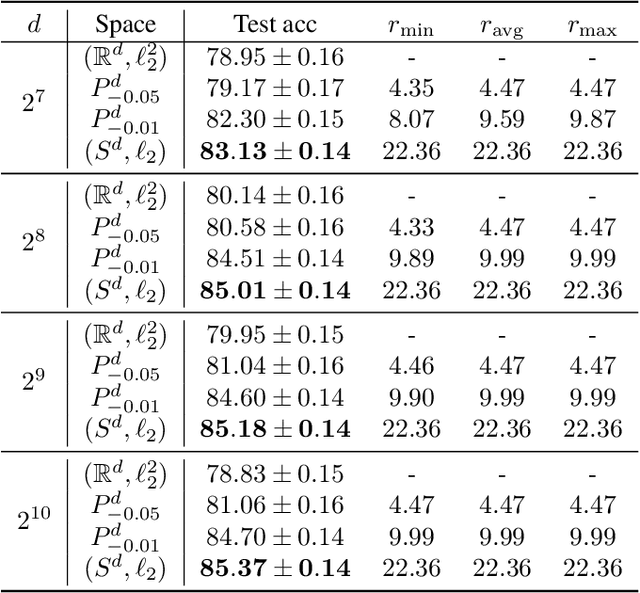
Recent research in representation learning has shown that hierarchical data lends itself to low-dimensional and highly informative representations in hyperbolic space. However, even if hyperbolic embeddings have gathered attention in image recognition, their optimization is prone to numerical hurdles. Further, it remains unclear which applications stand to benefit the most from the implicit bias imposed by hyperbolicity, when compared to traditional Euclidean features. In this paper, we focus on prototypical hyperbolic neural networks. In particular, the tendency of hyperbolic embeddings to converge to the boundary of the Poincar\'e ball in high dimensions and the effect this has on few-shot classification. We show that the best few-shot results are attained for hyperbolic embeddings at a common hyperbolic radius. In contrast to prior benchmark results, we demonstrate that better performance can be achieved by a fixed-radius encoder equipped with the Euclidean metric, regardless of the embedding dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge