Ben Chamberlain
Temporal Graph Networks for Deep Learning on Dynamic Graphs
Jun 18, 2020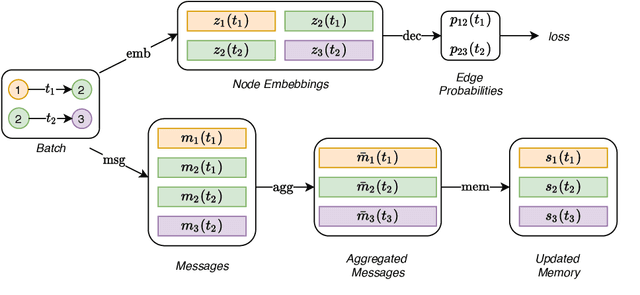
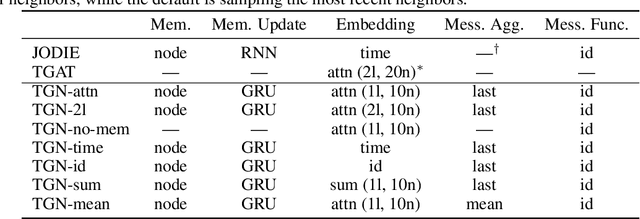
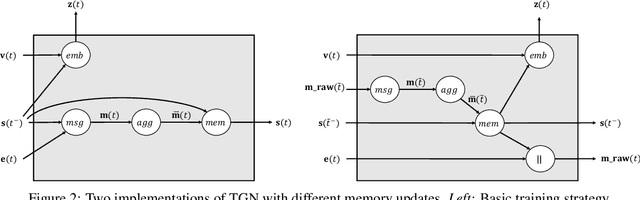
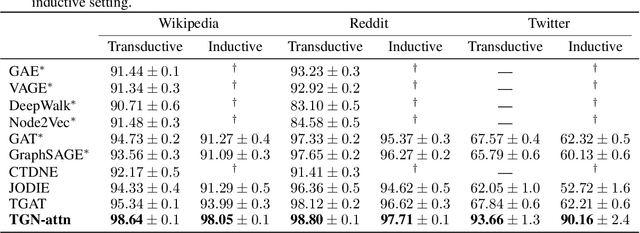
Abstract:Graph Neural Networks (GNNs) have recently become increasingly popular due to their ability to learn complex systems of relations or interactions arising in a broad spectrum of problems ranging from biology and particle physics to social networks and recommendation systems. Despite the plethora of different models for deep learning on graphs, few approaches have been proposed thus far for dealing with graphs that present some sort of dynamic nature (e.g. evolving features or connectivity over time). In this paper, we present Temporal Graph Networks (TGNs), a generic, efficient framework for deep learning on dynamic graphs represented as sequences of timed events. Thanks to a novel combination of memory modules and graph-based operators, TGNs are able to significantly outperform previous approaches being at the same time more computationally efficient. We furthermore show that several previous models for learning on dynamic graphs can be cast as specific instances of our framework. We perform a detailed ablation study of different components of our framework and devise the best configuration that achieves state-of-the-art performance on several transductive and inductive prediction tasks for dynamic graphs.
SIGN: Scalable Inception Graph Neural Networks
Apr 23, 2020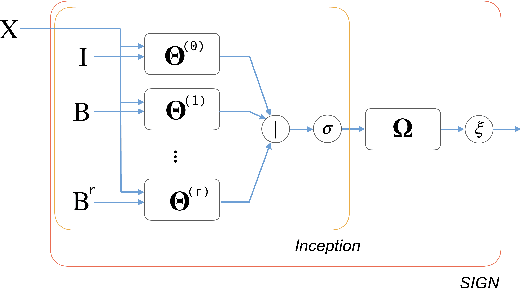


Abstract:Geometric deep learning, a novel class of machine learning algorithms extending classical deep learning architectures to non-Euclidean structured data such as manifolds and graphs, has recently been applied to a broad spectrum of problems ranging from computer graphics and chemistry to high energy physics and social media. In this paper, we propose SIGN, a scalable graph neural network analogous to the popular inception module used in classical convolutional architectures. We show that our architecture is able to effectively deal with large-scale graphs via pre-computed multi-scale neighborhood features. Extensive experimental evaluation on various open benchmarks shows the competitive performance of our approach compared to a variety of popular architectures, while requiring a fraction of training and inference time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge