Fabrizio Frasca
Learning on LLM Output Signatures for gray-box LLM Behavior Analysis
Mar 18, 2025Abstract:Large Language Models (LLMs) have achieved widespread adoption, yet our understanding of their behavior remains limited, particularly in detecting data contamination and hallucinations. While recently proposed probing techniques provide insights through activation analysis, they require "white-box" access to model internals, often unavailable. Current "gray-box" approaches typically analyze only the probability of the actual tokens in the sequence with simple task-specific heuristics. Importantly, these methods overlook the rich information contained in the full token distribution at each processing step. To address these limitations, we propose that gray-box analysis should leverage the complete observable output of LLMs, consisting of both the previously used token probabilities as well as the complete token distribution sequences - a unified data type we term LOS (LLM Output Signature). To this end, we develop a transformer-based approach to process LOS that theoretically guarantees approximation of existing techniques while enabling more nuanced analysis. Our approach achieves superior performance on hallucination and data contamination detection in gray-box settings, significantly outperforming existing baselines. Furthermore, it demonstrates strong transfer capabilities across datasets and LLMs, suggesting that LOS captures fundamental patterns in LLM behavior. Our code is available at: https://github.com/BarSGuy/LLM-Output-Signatures-Network.
Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks
Feb 20, 2025
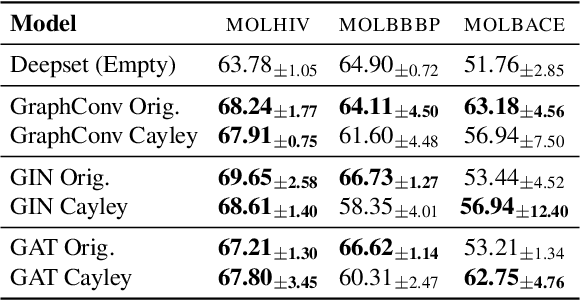
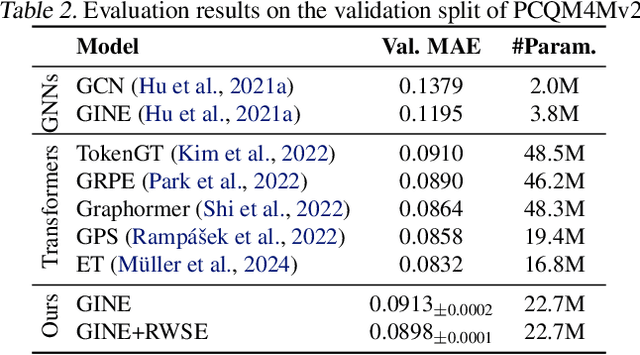
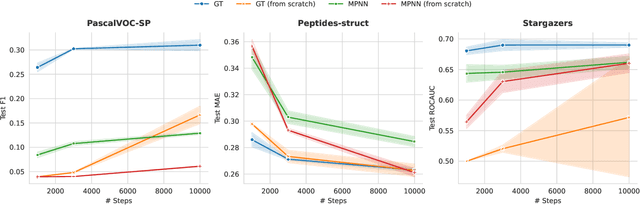
Abstract:While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.
Balancing Efficiency and Expressiveness: Subgraph GNNs with Walk-Based Centrality
Jan 06, 2025



Abstract:We propose an expressive and efficient approach that combines the strengths of two prominent extensions of Graph Neural Networks (GNNs): Subgraph GNNs and Structural Encodings (SEs). Our approach leverages walk-based centrality measures, both as a powerful form of SE and also as a subgraph selection strategy for Subgraph GNNs. By drawing a connection to perturbation analysis, we highlight the effectiveness of centrality-based sampling, and show it significantly reduces the computational burden associated with Subgraph GNNs. Further, we combine our efficient Subgraph GNN with SEs derived from the calculated centrality and demonstrate this hybrid approach, dubbed HyMN, gains in discriminative power. HyMN effectively addresses the expressiveness limitations of Message Passing Neural Networks (MPNNs) while mitigating the computational costs of Subgraph GNNs. Through a series of experiments on synthetic and real-world tasks, we show it outperforms other subgraph sampling approaches while being competitive with full-bag Subgraph GNNs and other state-of-the-art approaches with a notably reduced runtime.
Towards Foundation Models on Graphs: An Analysis on Cross-Dataset Transfer of Pretrained GNNs
Dec 23, 2024Abstract:To develop a preliminary understanding towards Graph Foundation Models, we study the extent to which pretrained Graph Neural Networks can be applied across datasets, an effort requiring to be agnostic to dataset-specific features and their encodings. We build upon a purely structural pretraining approach and propose an extension to capture feature information while still being feature-agnostic. We evaluate pretrained models on downstream tasks for varying amounts of training samples and choices of pretraining datasets. Our preliminary results indicate that embeddings from pretrained models improve generalization only with enough downstream data points and in a degree which depends on the quantity and properties of pretraining data. Feature information can lead to improvements, but currently requires some similarities between pretraining and downstream feature spaces.
Topological Blind Spots: Understanding and Extending Topological Deep Learning Through the Lens of Expressivity
Aug 10, 2024Abstract:Topological deep learning (TDL) facilitates learning from data represented by topological structures. The primary model utilized in this setting is higher-order message-passing (HOMP), which extends traditional graph message-passing neural networks (MPNN) to diverse topological domains. Given the significant expressivity limitations of MPNNs, our paper aims to explore both the strengths and weaknesses of HOMP's expressive power and subsequently design novel architectures to address these limitations. We approach this from several perspectives: First, we demonstrate HOMP's inability to distinguish between topological objects based on fundamental topological and metric properties such as diameter, orientability, planarity, and homology. Second, we show HOMP's limitations in fully leveraging the topological structure of objects constructed using common lifting and pooling operators on graphs. Finally, we compare HOMP's expressive power to hypergraph networks, which are the most extensively studied TDL methods. We then develop two new classes of TDL models: multi-cellular networks (MCN) and scalable multi-cellular networks (SMCN). These models draw inspiration from expressive graph architectures. While MCN can reach full expressivity but is highly unscalable, SMCN offers a more scalable alternative that still mitigates many of HOMP's expressivity limitations. Finally, we construct a synthetic dataset, where TDL models are tasked with separating pairs of topological objects based on basic topological properties. We demonstrate that while HOMP is unable to distinguish between any of the pairs in the dataset, SMCN successfully distinguishes all pairs, empirically validating our theoretical findings. Our work opens a new design space and new opportunities for TDL, paving the way for more expressive and versatile models.
A Flexible, Equivariant Framework for Subgraph GNNs via Graph Products and Graph Coarsening
Jun 13, 2024



Abstract:Subgraph Graph Neural Networks (Subgraph GNNs) enhance the expressivity of message-passing GNNs by representing graphs as sets of subgraphs. They have shown impressive performance on several tasks, but their complexity limits applications to larger graphs. Previous approaches suggested processing only subsets of subgraphs, selected either randomly or via learnable sampling. However, they make suboptimal subgraph selections or can only cope with very small subset sizes, inevitably incurring performance degradation. This paper introduces a new Subgraph GNNs framework to address these issues. We employ a graph coarsening function to cluster nodes into super-nodes with induced connectivity. The product between the coarsened and the original graph reveals an implicit structure whereby subgraphs are associated with specific sets of nodes. By running generalized message-passing on such graph product, our method effectively implements an efficient, yet powerful Subgraph GNN. Controlling the coarsening function enables meaningful selection of any number of subgraphs while, contrary to previous methods, being fully compatible with standard training techniques. Notably, we discover that the resulting node feature tensor exhibits new, unexplored permutation symmetries. We leverage this structure, characterize the associated linear equivariant layers and incorporate them into the layers of our Subgraph GNN architecture. Extensive experiments on multiple graph learning benchmarks demonstrate that our method is significantly more flexible than previous approaches, as it can seamlessly handle any number of subgraphs, while consistently outperforming baseline approaches.
Future Directions in Foundations of Graph Machine Learning
Feb 03, 2024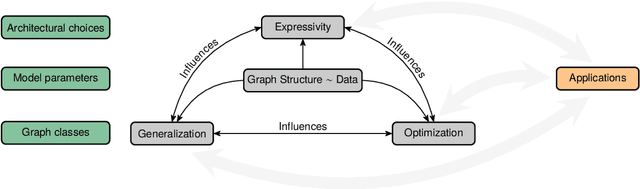
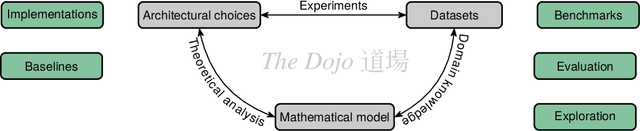
Abstract:Machine learning on graphs, especially using graph neural networks (GNNs), has seen a surge in interest due to the wide availability of graph data across a broad spectrum of disciplines, from life to social and engineering sciences. Despite their practical success, our theoretical understanding of the properties of GNNs remains highly incomplete. Recent theoretical advancements primarily focus on elucidating the coarse-grained expressive power of GNNs, predominantly employing combinatorial techniques. However, these studies do not perfectly align with practice, particularly in understanding the generalization behavior of GNNs when trained with stochastic first-order optimization techniques. In this position paper, we argue that the graph machine learning community needs to shift its attention to developing a more balanced theory of graph machine learning, focusing on a more thorough understanding of the interplay of expressive power, generalization, and optimization.
Edge Directionality Improves Learning on Heterophilic Graphs
May 17, 2023



Abstract:Graph Neural Networks (GNNs) have become the de-facto standard tool for modeling relational data. However, while many real-world graphs are directed, the majority of today's GNN models discard this information altogether by simply making the graph undirected. The reasons for this are historical: 1) many early variants of spectral GNNs explicitly required undirected graphs, and 2) the first benchmarks on homophilic graphs did not find significant gain from using direction. In this paper, we show that in heterophilic settings, treating the graph as directed increases the effective homophily of the graph, suggesting a potential gain from the correct use of directionality information. To this end, we introduce Directed Graph Neural Network (Dir-GNN), a novel general framework for deep learning on directed graphs. Dir-GNN can be used to extend any Message Passing Neural Network (MPNN) to account for edge directionality information by performing separate aggregations of the incoming and outgoing edges. We prove that Dir-GNN matches the expressivity of the Directed Weisfeiler-Lehman test, exceeding that of conventional MPNNs. In extensive experiments, we validate that while our framework leaves performance unchanged on homophilic datasets, it leads to large gains over base models such as GCN, GAT and GraphSage on heterophilic benchmarks, outperforming much more complex methods and achieving new state-of-the-art results.
Graph Positional Encoding via Random Feature Propagation
Mar 08, 2023Abstract:Two main families of node feature augmentation schemes have been explored for enhancing GNNs: random features and spectral positional encoding. Surprisingly, however, there is still no clear understanding of the relation between these two augmentation schemes. Here we propose a novel family of positional encoding schemes which draws a link between the above two approaches and improves over both. The new approach, named Random Feature Propagation (RFP), is inspired by the power iteration method and its generalizations. It concatenates several intermediate steps of an iterative algorithm for computing the dominant eigenvectors of a propagation matrix, starting from random node features. Notably, these propagation steps are based on graph-dependent propagation operators that can be either predefined or learned. We explore the theoretical and empirical benefits of RFP. First, we provide theoretical justifications for using random features, for incorporating early propagation steps, and for using multiple random initializations. Then, we empirically demonstrate that RFP significantly outperforms both spectral PE and random features in multiple node classification and graph classification benchmarks.
Graph Neural Networks for Link Prediction with Subgraph Sketching
Oct 03, 2022
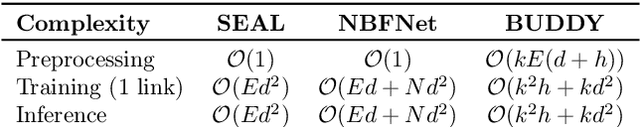
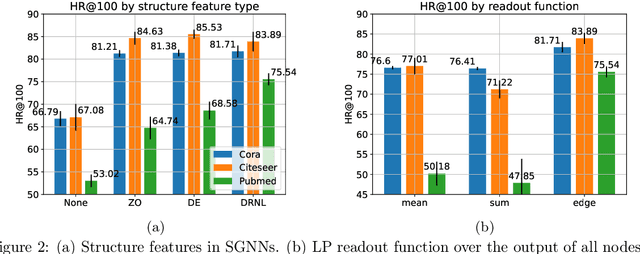
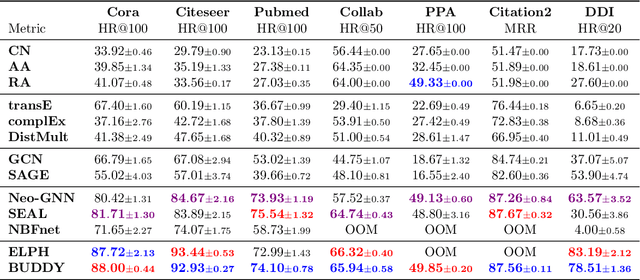
Abstract:Many Graph Neural Networks (GNNs) perform poorly compared to simple heuristics on Link Prediction (LP) tasks. This is due to limitations in expressive power such as the inability to count triangles (the backbone of most LP heuristics) and because they can not distinguish automorphic nodes (those having identical structural roles). Both expressiveness issues can be alleviated by learning link (rather than node) representations and incorporating structural features such as triangle counts. Since explicit link representations are often prohibitively expensive, recent works resorted to subgraph-based methods, which have achieved state-of-the-art performance for LP, but suffer from poor efficiency due to high levels of redundancy between subgraphs. We analyze the components of subgraph GNN (SGNN) methods for link prediction. Based on our analysis, we propose a novel full-graph GNN called ELPH (Efficient Link Prediction with Hashing) that passes subgraph sketches as messages to approximate the key components of SGNNs without explicit subgraph construction. ELPH is provably more expressive than Message Passing GNNs (MPNNs). It outperforms existing SGNN models on many standard LP benchmarks while being orders of magnitude faster. However, it shares the common GNN limitation that it is only efficient when the dataset fits in GPU memory. Accordingly, we develop a highly scalable model, called BUDDY, which uses feature precomputation to circumvent this limitation without sacrificing predictive performance. Our experiments show that BUDDY also outperforms SGNNs on standard LP benchmarks while being highly scalable and faster than ELPH.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge