Query Languages for Machine-Learning Models

In this paper, I discuss two logics for weighted finite structures: first-order logic with summation (FO(SUM)) and its recursive extension IFP(SUM). These logics originate from foundational work by Grädel, Gurevich, and Meer in the 1990s. In recent joint work with Standke, Steegmans, and Van den Bussche, we have investigated these logics as query languages for machine learning models, specifically neural networks, which are naturally represented as weighted graphs. I present illustrative examples of queries to neural networks that can be expressed in these logics and discuss fundamental results on their expressiveness and computational complexity.

Recursive querying of neural networks via weighted structures

Expressive querying of machine learning models - viewed as a form of intentional data - enables their verification and interpretation using declarative languages, thereby making learned representations of data more accessible. Motivated by the querying of feedforward neural networks, we investigate logics for weighted structures. In the absence of a bound on neural network depth, such logics must incorporate recursion; thereto we revisit the functional fixpoint mechanism proposed by Grädel and Gurevich. We adopt it in a Datalog-like syntax; we extend normal forms for fixpoint logics to weighted structures; and show an equivalent "loose" fixpoint mechanism that allows values of inductively defined weight functions to be overwritten. We propose a "scalar" restriction of functional fixpoint logic, of polynomial-time data complexity, and show it can express all PTIME model-agnostic queries over reduced networks with polynomially bounded weights. In contrast, we show that very simple model-agnostic queries are already NP-complete. Finally, we consider transformations of weighted structures by iterated transductions.

Learning from Algorithm Feedback: One-Shot SAT Solver Guidance with GNNs

Boolean Satisfiability (SAT) solvers are foundational to computer science, yet their performance typically hinges on hand-crafted heuristics. This work introduces Reinforcement Learning from Algorithm Feedback (RLAF) as a paradigm for learning to guide SAT solver branching heuristics with Graph Neural Networks (GNNs). Central to our approach is a novel and generic mechanism for injecting inferred variable weights and polarities into the branching heuristics of existing SAT solvers. In a single forward pass, a GNN assigns these parameters to all variables. Casting this one-shot guidance as a reinforcement learning problem lets us train the GNN with off-the-shelf policy-gradient methods, such as GRPO, directly using the solver's computational cost as the sole reward signal. Extensive evaluations demonstrate that RLAF-trained policies significantly reduce the mean solve times of different base solvers across diverse SAT problem distributions, achieving more than a 2x speedup in some cases, while generalizing effectively to larger and harder problems after training. Notably, these policies consistently outperform expert-supervised approaches based on learning handcrafted weighting heuristics, offering a promising path towards data-driven heuristic design in combinatorial optimization.

Repetition Makes Perfect: Recurrent Sum-GNNs Match Message Passing Limit

We provide first tight bounds for the expressivity of Recurrent Graph Neural Networks (recurrent GNNs) with finite-precision parameters. We prove that recurrent GNNs, with sum aggregation and ReLU activation, can emulate any graph algorithm that respects the natural message-passing invariance induced by the color refinement (or Weisfeiler-Leman) algorithm. While it is well known that the expressive power of GNNs is limited by this invariance [Morris et al., AAAI 2019; Xu et al., ICLR 2019], we establish that recurrent GNNs can actually reach this limit. This is in contrast to non-recurrent GNNs, which have the power of Weisfeiler-Leman only in a very weak, "non-uniform", sense where every graph size requires a different GNN model to compute with. The emulation we construct introduces only a polynomial overhead in both time and space. Furthermore, we show that by incorporating random initialization, recurrent GNNs can emulate all graph algorithms, implying in particular that any graph algorithm with polynomial-time complexity can be emulated by a recurrent GNN with random initialization, running in polynomial time.

GraphXForm: Graph transformer for computer-aided molecular design with application to extraction

Generative deep learning has become pivotal in molecular design for drug discovery and materials science. A widely used paradigm is to pretrain neural networks on string representations of molecules and fine-tune them using reinforcement learning on specific objectives. However, string-based models face challenges in ensuring chemical validity and enforcing structural constraints like the presence of specific substructures. We propose to instead combine graph-based molecular representations, which can naturally ensure chemical validity, with transformer architectures, which are highly expressive and capable of modeling long-range dependencies between atoms. Our approach iteratively modifies a molecular graph by adding atoms and bonds, which ensures chemical validity and facilitates the incorporation of structural constraints. We present GraphXForm, a decoder-only graph transformer architecture, which is pretrained on existing compounds and then fine-tuned using a new training algorithm that combines elements of the deep cross-entropy method with self-improvement learning from language modeling, allowing stable fine-tuning of deep transformers with many layers. We evaluate GraphXForm on two solvent design tasks for liquid-liquid extraction, showing that it outperforms four state-of-the-art molecular design techniques, while it can flexibly enforce structural constraints or initiate the design from existing molecular structures.

Query languages for neural networks

We lay the foundations for a database-inspired approach to interpreting and understanding neural network models by querying them using declarative languages. Towards this end we study different query languages, based on first-order logic, that mainly differ in their access to the neural network model. First-order logic over the reals naturally yields a language which views the network as a black box; only the input--output function defined by the network can be queried. This is essentially the approach of constraint query languages. On the other hand, a white-box language can be obtained by viewing the network as a weighted graph, and extending first-order logic with summation over weight terms. The latter approach is essentially an abstraction of SQL. In general, the two approaches are incomparable in expressive power, as we will show. Under natural circumstances, however, the white-box approach can subsume the black-box approach; this is our main result. We prove the result concretely for linear constraint queries over real functions definable by feedforward neural networks with a fixed number of hidden layers and piecewise linear activation functions.

Distinguished In Uniform: Self Attention Vs. Virtual Nodes

Graph Transformers (GTs) such as SAN and GPS are graph processing models that combine Message-Passing GNNs (MPGNNs) with global Self-Attention. They were shown to be universal function approximators, with two reservations: 1. The initial node features must be augmented with certain positional encodings. 2. The approximation is non-uniform: Graphs of different sizes may require a different approximating network. We first clarify that this form of universality is not unique to GTs: Using the same positional encodings, also pure MPGNNs and even 2-layer MLPs are non-uniform universal approximators. We then consider uniform expressivity: The target function is to be approximated by a single network for graphs of all sizes. There, we compare GTs to the more efficient MPGNN + Virtual Node architecture. The essential difference between the two model definitions is in their global computation method -- Self-Attention Vs Virtual Node. We prove that none of the models is a uniform-universal approximator, before proving our main result: Neither model's uniform expressivity subsumes the other's. We demonstrate the theory with experiments on synthetic data. We further augment our study with real-world datasets, observing mixed results which indicate no clear ranking in practice as well.

Are Targeted Messages More Effective?

Graph neural networks (GNN) are deep learning architectures for graphs. Essentially, a GNN is a distributed message passing algorithm, which is controlled by parameters learned from data. It operates on the vertices of a graph: in each iteration, vertices receive a message on each incoming edge, aggregate these messages, and then update their state based on their current state and the aggregated messages. The expressivity of GNNs can be characterised in terms of certain fragments of first-order logic with counting and the Weisfeiler-Lehman algorithm. The core GNN architecture comes in two different versions. In the first version, a message only depends on the state of the source vertex, whereas in the second version it depends on the states of the source and target vertices. In practice, both of these versions are used, but the theory of GNNs so far mostly focused on the first one. On the logical side, the two versions correspond to two fragments of first-order logic with counting that we call modal and guarded. The question whether the two versions differ in their expressivity has been mostly overlooked in the GNN literature and has only been asked recently (Grohe, LICS'23). We answer this question here. It turns out that the answer is not as straightforward as one might expect. By proving that the modal and guarded fragment of first-order logic with counting have the same expressivity over labelled undirected graphs, we show that in a non-uniform setting the two GNN versions have the same expressivity. However, we also prove that in a uniform setting the second version is strictly more expressive.

Future Directions in Foundations of Graph Machine Learning

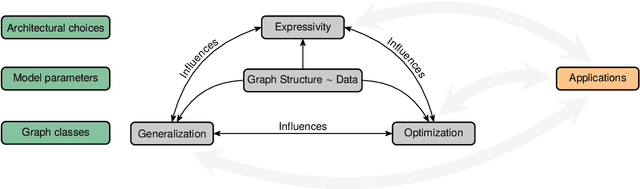
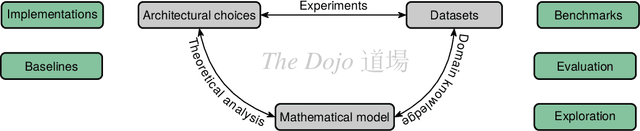
Machine learning on graphs, especially using graph neural networks (GNNs), has seen a surge in interest due to the wide availability of graph data across a broad spectrum of disciplines, from life to social and engineering sciences. Despite their practical success, our theoretical understanding of the properties of GNNs remains highly incomplete. Recent theoretical advancements primarily focus on elucidating the coarse-grained expressive power of GNNs, predominantly employing combinatorial techniques. However, these studies do not perfectly align with practice, particularly in understanding the generalization behavior of GNNs when trained with stochastic first-order optimization techniques. In this position paper, we argue that the graph machine learning community needs to shift its attention to developing a more balanced theory of graph machine learning, focusing on a more thorough understanding of the interplay of expressive power, generalization, and optimization.

Selecting Walk Schemes for Database Embedding

Machinery for data analysis often requires a numeric representation of the input. Towards that, a common practice is to embed components of structured data into a high-dimensional vector space. We study the embedding of the tuples of a relational database, where existing techniques are often based on optimization tasks over a collection of random walks from the database. The focus of this paper is on the recent FoRWaRD algorithm that is designed for dynamic databases, where walks are sampled by following foreign keys between tuples. Importantly, different walks have different schemas, or "walk schemes", that are derived by listing the relations and attributes along the walk. Also importantly, different walk schemes describe relationships of different natures in the database. We show that by focusing on a few informative walk schemes, we can obtain tuple embedding significantly faster, while retaining the quality. We define the problem of scheme selection for tuple embedding, devise several approaches and strategies for scheme selection, and conduct a thorough empirical study of the performance over a collection of downstream tasks. Our results confirm that with effective strategies for scheme selection, we can obtain high-quality embeddings considerably (e.g., three times) faster, preserve the extensibility to newly inserted tuples, and even achieve an increase in the precision of some tasks.