Predicting the Temperature-Dependent CMC of Surfactant Mixtures with Graph Neural Networks

Surfactants are key ingredients in foaming and cleansing products across various industries such as personal and home care, industrial cleaning, and more, with the critical micelle concentration (CMC) being of major interest. Predictive models for CMC of pure surfactants have been developed based on recent ML methods, however, in practice surfactant mixtures are typically used due to to performance, environmental, and cost reasons. This requires accounting for synergistic/antagonistic interactions between surfactants; however, predictive ML models for a wide spectrum of mixtures are missing so far. Herein, we develop a graph neural network (GNN) framework for surfactant mixtures to predict the temperature-dependent CMC. We collect data for 108 surfactant binary mixtures, to which we add data for pure species from our previous work [Brozos et al. (2024), J. Chem. Theory Comput.]. We then develop and train GNNs and evaluate their accuracy across different prediction test scenarios for binary mixtures relevant to practical applications. The final GNN models demonstrate very high predictive performance when interpolating between different mixture compositions and for new binary mixtures with known species. Extrapolation to binary surfactant mixtures where either one or both surfactant species are not seen before, yields accurate results for the majority of surfactant systems. We further find superior accuracy of the GNN over a semi-empirical model based on activity coefficients, which has been widely used to date. We then explore if GNN models trained solely on binary mixture and pure species data can also accurately predict the CMCs of ternary mixtures. Finally, we experimentally measure the CMC of 4 commercial surfactants that contain up to four species and industrial relevant mixtures and find a very good agreement between measured and predicted CMC values.

GraphXForm: Graph transformer for computer-aided molecular design with application to extraction

Generative deep learning has become pivotal in molecular design for drug discovery and materials science. A widely used paradigm is to pretrain neural networks on string representations of molecules and fine-tune them using reinforcement learning on specific objectives. However, string-based models face challenges in ensuring chemical validity and enforcing structural constraints like the presence of specific substructures. We propose to instead combine graph-based molecular representations, which can naturally ensure chemical validity, with transformer architectures, which are highly expressive and capable of modeling long-range dependencies between atoms. Our approach iteratively modifies a molecular graph by adding atoms and bonds, which ensures chemical validity and facilitates the incorporation of structural constraints. We present GraphXForm, a decoder-only graph transformer architecture, which is pretrained on existing compounds and then fine-tuned using a new training algorithm that combines elements of the deep cross-entropy method with self-improvement learning from language modeling, allowing stable fine-tuning of deep transformers with many layers. We evaluate GraphXForm on two solvent design tasks for liquid-liquid extraction, showing that it outperforms four state-of-the-art molecular design techniques, while it can flexibly enforce structural constraints or initiate the design from existing molecular structures.

Predicting the Temperature Dependence of Surfactant CMCs Using Graph Neural Networks

The critical micelle concentration (CMC) of surfactant molecules is an essential property for surfactant applications in industry. Recently, classical QSPR and Graph Neural Networks (GNNs), a deep learning technique, have been successfully applied to predict the CMC of surfactants at room temperature. However, these models have not yet considered the temperature dependency of the CMC, which is highly relevant for practical applications. We herein develop a GNN model for temperature-dependent CMC prediction of surfactants. We collect about 1400 data points from public sources for all surfactant classes, i.e., ionic, nonionic, and zwitterionic, at multiple temperatures. We test the predictive quality of the model for following scenarios: i) when CMC data for surfactants are present in the training of the model in at least one different temperature, and ii) CMC data for surfactants are not present in the training, i.e., generalizing to unseen surfactants. In both test scenarios, our model exhibits a high predictive performance of R$^2 \geq $ 0.94 on test data. We also find that the model performance varies by surfactant class. Finally, we evaluate the model for sugar-based surfactants with complex molecular structures, as these represent a more sustainable alternative to synthetic surfactants and are therefore of great interest for future applications in the personal and home care industries.

Graph Neural Networks for Surfactant Multi-Property Prediction

Surfactants are of high importance in different industrial sectors such as cosmetics, detergents, oil recovery and drug delivery systems. Therefore, many quantitative structure-property relationship (QSPR) models have been developed for surfactants. Each predictive model typically focuses on one surfactant class, mostly nonionics. Graph Neural Networks (GNNs) have exhibited a great predictive performance for property prediction of ionic liquids, polymers and drugs in general. Specifically for surfactants, GNNs can successfully predict critical micelle concentration (CMC), a key surfactant property associated with micellization. A key factor in the predictive ability of QSPR and GNN models is the data available for training. Based on extensive literature search, we create the largest available CMC database with 429 molecules and the first large data collection for surface excess concentration ($\Gamma$$_{m}$), another surfactant property associated with foaming, with 164 molecules. Then, we develop GNN models to predict the CMC and $\Gamma$$_{m}$ and we explore different learning approaches, i.e., single- and multi-task learning, as well as different training strategies, namely ensemble and transfer learning. We find that a multi-task GNN with ensemble learning trained on all $\Gamma$$_{m}$ and CMC data performs best. Finally, we test the ability of our CMC model to generalize on industrial grade pure component surfactants. The GNN yields highly accurate predictions for CMC, showing great potential for future industrial applications.

Gibbs-Duhem-Informed Neural Networks for Binary Activity Coefficient Prediction

We propose Gibbs-Duhem-informed neural networks for the prediction of binary activity coefficients at varying compositions. That is, we include the Gibbs-Duhem equation explicitly in the loss function for training neural networks, which is straightforward in standard machine learning (ML) frameworks enabling automatic differentiation. In contrast to recent hybrid ML approaches, our approach does not rely on embedding a specific thermodynamic model inside the neural network and corresponding prediction limitations. Rather, Gibbs-Duhem consistency serves as regularization, with the flexibility of ML models being preserved. Our results show increased thermodynamic consistency and generalization capabilities for activity coefficient predictions by Gibbs-Duhem-informed graph neural networks and matrix completion methods. We also find that the model architecture, particularly the activation function, can have a strong influence on the prediction quality. The approach can be easily extended to account for other thermodynamic consistency conditions.

Physical Pooling Functions in Graph Neural Networks for Molecular Property Prediction

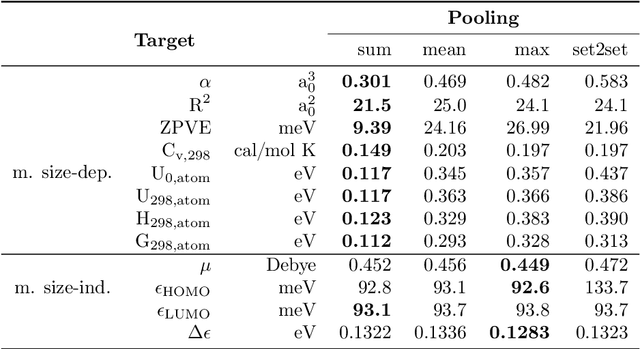
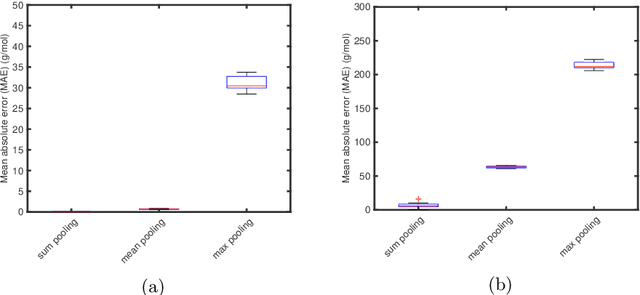
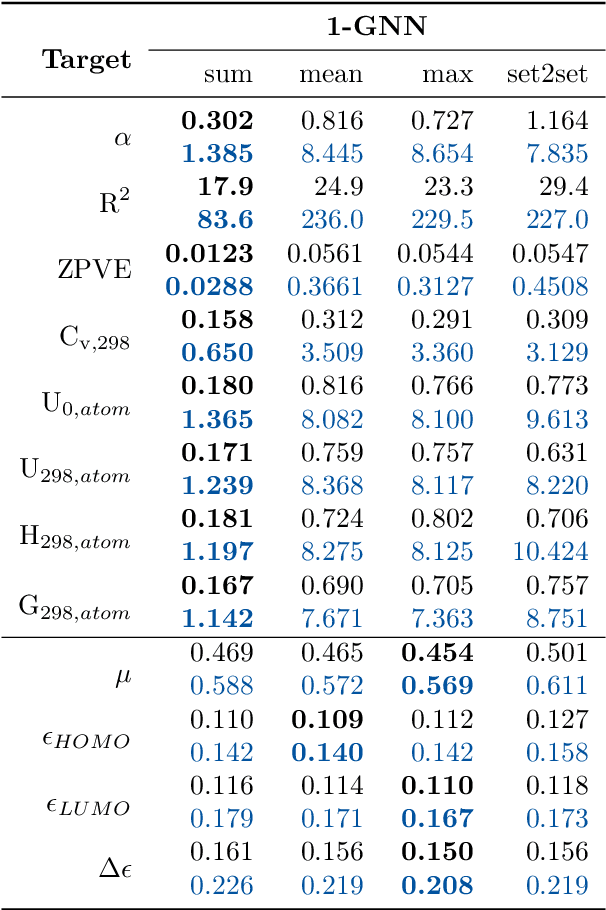
Graph neural networks (GNNs) are emerging in chemical engineering for the end-to-end learning of physicochemical properties based on molecular graphs. A key element of GNNs is the pooling function which combines atom feature vectors into molecular fingerprints. Most previous works use a standard pooling function to predict a variety of properties. However, unsuitable pooling functions can lead to unphysical GNNs that poorly generalize. We compare and select meaningful GNN pooling methods based on physical knowledge about the learned properties. The impact of physical pooling functions is demonstrated with molecular properties calculated from quantum mechanical computations. We also compare our results to the recent set2set pooling approach. We recommend using sum pooling for the prediction of properties that depend on molecular size and compare pooling functions for properties that are molecular size-independent. Overall, we show that the use of physical pooling functions significantly enhances generalization.

Graph neural networks for the prediction of molecular structure-property relationships

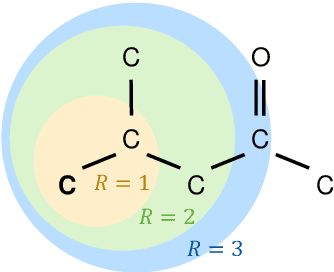
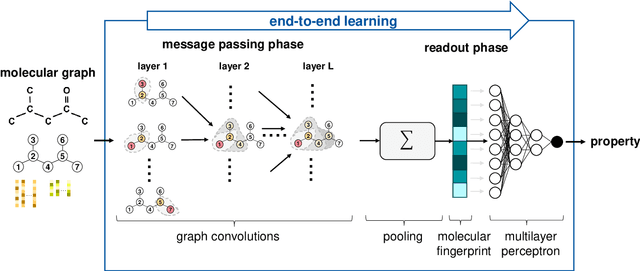
Molecular property prediction is of crucial importance in many disciplines such as drug discovery, molecular biology, or material and process design. The frequently employed quantitative structure-property/activity relationships (QSPRs/QSARs) characterize molecules by descriptors which are then mapped to the properties of interest via a linear or nonlinear model. In contrast, graph neural networks, a novel machine learning method, directly work on the molecular graph, i.e., a graph representation where atoms correspond to nodes and bonds correspond to edges. GNNs allow to learn properties in an end-to-end fashion, thereby avoiding the need for informative descriptors as in QSPRs/QSARs. GNNs have been shown to achieve state-of-the-art prediction performance on various property predictions tasks and represent an active field of research. We describe the fundamentals of GNNs and demonstrate the application of GNNs via two examples for molecular property prediction.

Graph Neural Networks for Temperature-Dependent Activity Coefficient Prediction of Solutes in Ionic Liquids

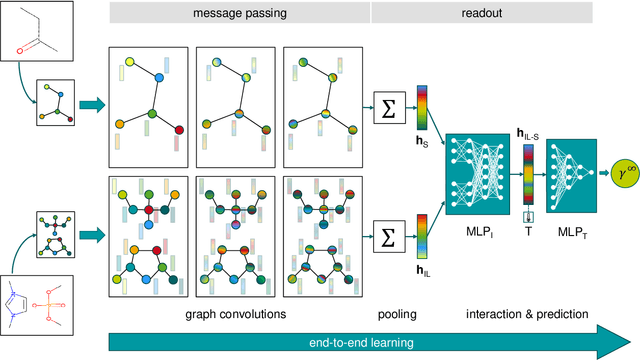
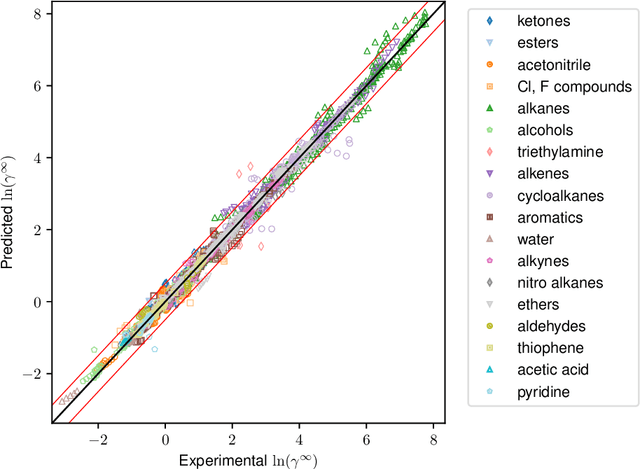
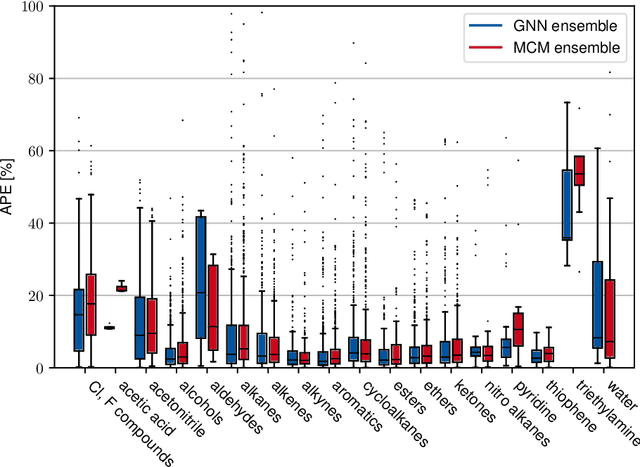
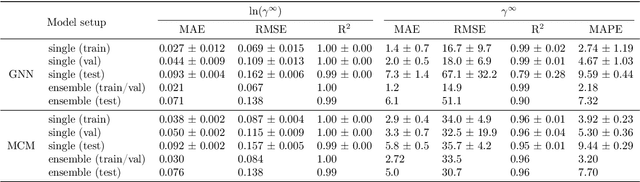
Ionic liquids (ILs) are important solvents for sustainable processes and predicting activity coefficients (ACs) of solutes in ILs is needed. Recently, matrix completion methods (MCMs), transformers, and graph neural networks (GNNs) have shown high accuracy in predicting ACs of binary mixtures, superior to well-established models, e.g., COSMO-RS and UNIFAC. GNNs are particularly promising here as they learn a molecular graph-to-property relationship without pretraining, typically required for transformers, and are, unlike MCMs, applicable to molecules not included in training. For ILs, however, GNN applications are currently missing. Herein, we present a GNN to predict temperature-dependent infinite dilution ACs of solutes in ILs. We train the GNN on a database including more than 40,000 AC values and compare it to a state-of-the-art MCM. The GNN and MCM achieve similar high prediction performance, with the GNN additionally enabling high-quality predictions for ACs of solutions that contain ILs and solutes not considered during training.

Graph Machine Learning for Design of High-Octane Fuels

Fuels with high-knock resistance enable modern spark-ignition engines to achieve high efficiency and thus low CO2 emissions. Identification of molecules with desired autoignition properties indicated by a high research octane number and a high octane sensitivity is therefore of great practical relevance and can be supported by computer-aided molecular design (CAMD). Recent developments in the field of graph machine learning (graph-ML) provide novel, promising tools for CAMD. We propose a modular graph-ML CAMD framework that integrates generative graph-ML models with graph neural networks and optimization, enabling the design of molecules with desired ignition properties in a continuous molecular space. In particular, we explore the potential of Bayesian optimization and genetic algorithms in combination with generative graph-ML models. The graph-ML CAMD framework successfully identifies well-established high-octane components. It also suggests new candidates, one of which we experimentally investigate and use to illustrate the need for further auto-ignition training data.