Physics-Informed Neural Networks for Dynamic Process Operations with Limited Physical Knowledge and Data

In chemical engineering, process data is often expensive to acquire, and complex phenomena are difficult to model rigorously, rendering both entirely data-driven and purely mechanistic modeling approaches impractical. We explore using physics-informed neural networks (PINNs) for modeling dynamic processes governed by differential-algebraic equation systems when process data is scarce and complete mechanistic knowledge is missing. In particular, we focus on estimating states for which neither direct observational data nor constitutive equations are available. For demonstration purposes, we study a continuously stirred tank reactor and a liquid-liquid separator. We find that PINNs can infer unmeasured states with reasonable accuracy, and they generalize better in low-data scenarios than purely data-driven models. We thus show that PINNs, similar to hybrid mechanistic/data-driven models, are capable of modeling processes when relatively few experimental data and only partially known mechanistic descriptions are available, and conclude that they constitute a promising avenue that warrants further investigation.

Task-optimal data-driven surrogate models for eNMPC via differentiable simulation and optimization

We present a method for end-to-end learning of Koopman surrogate models for optimal performance in control. In contrast to previous contributions that employ standard reinforcement learning (RL) algorithms, we use a training algorithm that exploits the potential differentiability of environments based on mechanistic simulation models. We evaluate the performance of our method by comparing it to that of other controller type and training algorithm combinations on a literature known eNMPC case study. Our method exhibits superior performance on this problem, thereby constituting a promising avenue towards more capable controllers that employ dynamic surrogate models.

Multivariate Scenario Generation of Day-Ahead Electricity Prices using Normalizing Flows

Trading on electricity markets requires accurate information about the realization of electricity prices and the uncertainty attached to the predictions. We present a probabilistic forecasting approach for day-ahead electricity prices using the fully data-driven deep generative model called normalizing flows. Our modeling approach generates full-day scenarios of day-ahead electricity prices based on conditional features such as residual load forecasts. Furthermore, we propose extended feature sets of prior realizations and a periodic retraining scheme that allows the normalizing flow to adapt to the changing conditions of modern electricity markets. In particular, we investigate the impact of the energy crisis ensuing from the Russian invasion of Ukraine. Our results highlight that the normalizing flow generates high-quality scenarios that reproduce the true price distribution and yield highly accurate forecasts. Additionally, our analysis highlights how our improvements towards adaptations in changing regimes allow the normalizing flow to adapt to changing market conditions and enables continued sampling of high-quality day-ahead price scenarios.

End-to-End Reinforcement Learning of Koopman Models for Economic Nonlinear MPC

(Economic) nonlinear model predictive control ((e)NMPC) requires dynamic system models that are sufficiently accurate in all relevant state-space regions. These models must also be computationally cheap enough to ensure real-time tractability. Data-driven surrogate models for mechanistic models can be used to reduce the computational burden of (e)NMPC; however, such models are typically trained by system identification for maximum average prediction accuracy on simulation samples and perform suboptimally as part of actual (e)NMPC. We present a method for end-to-end reinforcement learning of dynamic surrogate models for optimal performance in (e)NMPC applications, resulting in predictive controllers that strike a favorable balance between control performance and computational demand. We validate our method on two applications derived from an established nonlinear continuous stirred-tank reactor model. We compare the controller performance to that of MPCs utilizing models trained by the prevailing maximum prediction accuracy paradigm, and model-free neural network controllers trained using reinforcement learning. We show that our method matches the performance of the model-free neural network controllers while consistently outperforming models derived from system identification. Additionally, we show that the MPC policies can react to changes in the control setting without retraining.

A Recursively Recurrent Neural Network (R2N2) Architecture for Learning Iterative Algorithms

Meta-learning of numerical algorithms for a given task consist of the data-driven identification and adaptation of an algorithmic structure and the associated hyperparameters. To limit the complexity of the meta-learning problem, neural architectures with a certain inductive bias towards favorable algorithmic structures can, and should, be used. We generalize our previously introduced Runge-Kutta neural network to a recursively recurrent neural network (R2N2) superstructure for the design of customized iterative algorithms. In contrast to off-the-shelf deep learning approaches, it features a distinct division into modules for generation of information and for the subsequent assembly of this information towards a solution. Local information in the form of a subspace is generated by subordinate, inner, iterations of recurrent function evaluations starting at the current outer iterate. The update to the next outer iterate is computed as a linear combination of these evaluations, reducing the residual in this space, and constitutes the output of the network. We demonstrate that regular training of the weight parameters inside the proposed superstructure on input/output data of various computational problem classes yields iterations similar to Krylov solvers for linear equation systems, Newton-Krylov solvers for nonlinear equation systems, and Runge-Kutta integrators for ordinary differential equations. Due to its modularity, the superstructure can be readily extended with functionalities needed to represent more general classes of iterative algorithms traditionally based on Taylor series expansions.

Physical Pooling Functions in Graph Neural Networks for Molecular Property Prediction

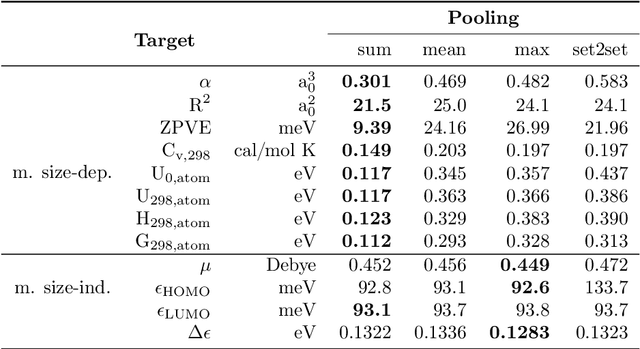
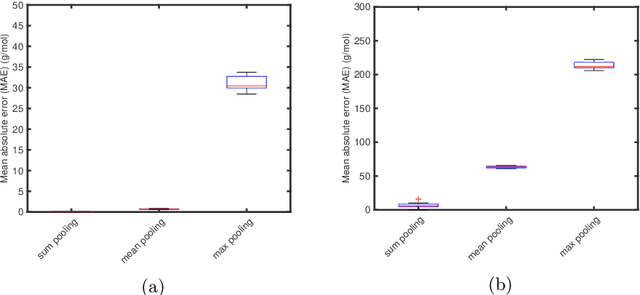
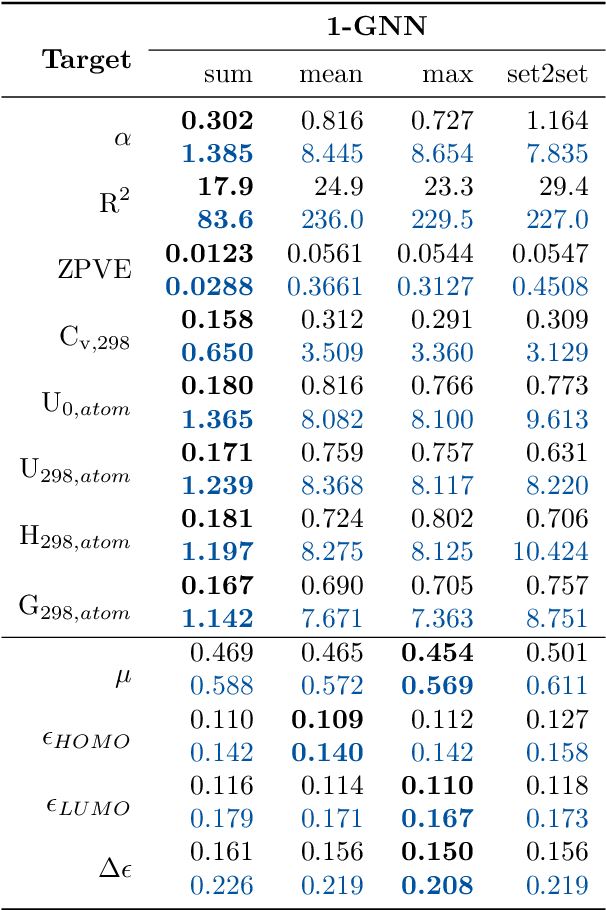
Graph neural networks (GNNs) are emerging in chemical engineering for the end-to-end learning of physicochemical properties based on molecular graphs. A key element of GNNs is the pooling function which combines atom feature vectors into molecular fingerprints. Most previous works use a standard pooling function to predict a variety of properties. However, unsuitable pooling functions can lead to unphysical GNNs that poorly generalize. We compare and select meaningful GNN pooling methods based on physical knowledge about the learned properties. The impact of physical pooling functions is demonstrated with molecular properties calculated from quantum mechanical computations. We also compare our results to the recent set2set pooling approach. We recommend using sum pooling for the prediction of properties that depend on molecular size and compare pooling functions for properties that are molecular size-independent. Overall, we show that the use of physical pooling functions significantly enhances generalization.

Graph neural networks for the prediction of molecular structure-property relationships

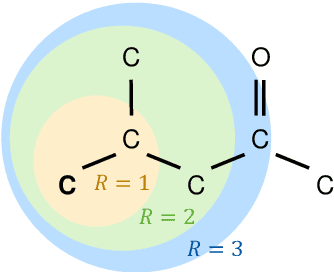
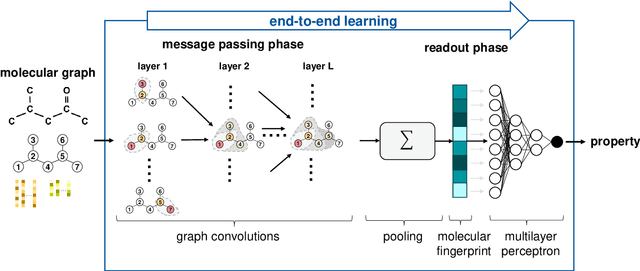
Molecular property prediction is of crucial importance in many disciplines such as drug discovery, molecular biology, or material and process design. The frequently employed quantitative structure-property/activity relationships (QSPRs/QSARs) characterize molecules by descriptors which are then mapped to the properties of interest via a linear or nonlinear model. In contrast, graph neural networks, a novel machine learning method, directly work on the molecular graph, i.e., a graph representation where atoms correspond to nodes and bonds correspond to edges. GNNs allow to learn properties in an end-to-end fashion, thereby avoiding the need for informative descriptors as in QSPRs/QSARs. GNNs have been shown to achieve state-of-the-art prediction performance on various property predictions tasks and represent an active field of research. We describe the fundamentals of GNNs and demonstrate the application of GNNs via two examples for molecular property prediction.

Graph Neural Networks for Temperature-Dependent Activity Coefficient Prediction of Solutes in Ionic Liquids

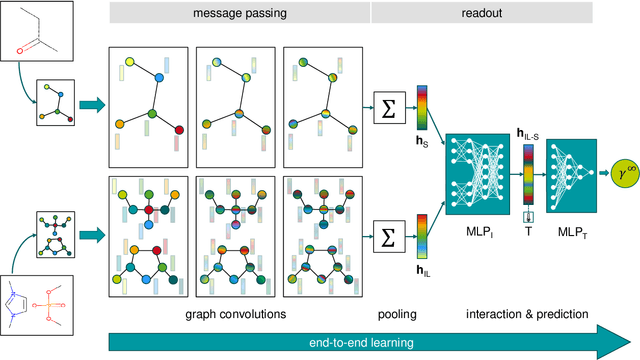
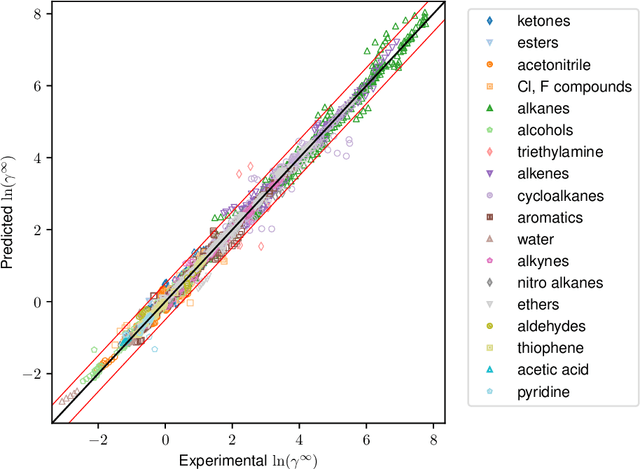
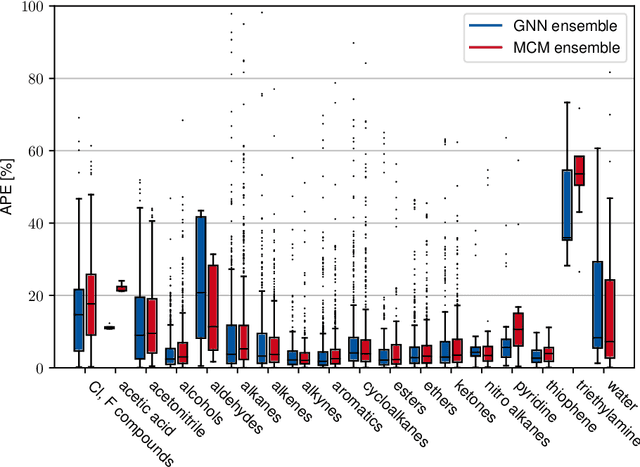
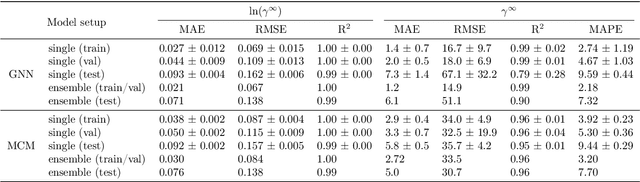
Ionic liquids (ILs) are important solvents for sustainable processes and predicting activity coefficients (ACs) of solutes in ILs is needed. Recently, matrix completion methods (MCMs), transformers, and graph neural networks (GNNs) have shown high accuracy in predicting ACs of binary mixtures, superior to well-established models, e.g., COSMO-RS and UNIFAC. GNNs are particularly promising here as they learn a molecular graph-to-property relationship without pretraining, typically required for transformers, and are, unlike MCMs, applicable to molecules not included in training. For ILs, however, GNN applications are currently missing. Herein, we present a GNN to predict temperature-dependent infinite dilution ACs of solutes in ILs. We train the GNN on a database including more than 40,000 AC values and compare it to a state-of-the-art MCM. The GNN and MCM achieve similar high prediction performance, with the GNN additionally enabling high-quality predictions for ACs of solutions that contain ILs and solutes not considered during training.

Graph Machine Learning for Design of High-Octane Fuels

Fuels with high-knock resistance enable modern spark-ignition engines to achieve high efficiency and thus low CO2 emissions. Identification of molecules with desired autoignition properties indicated by a high research octane number and a high octane sensitivity is therefore of great practical relevance and can be supported by computer-aided molecular design (CAMD). Recent developments in the field of graph machine learning (graph-ML) provide novel, promising tools for CAMD. We propose a modular graph-ML CAMD framework that integrates generative graph-ML models with graph neural networks and optimization, enabling the design of molecules with desired ignition properties in a continuous molecular space. In particular, we explore the potential of Bayesian optimization and genetic algorithms in combination with generative graph-ML models. The graph-ML CAMD framework successfully identifies well-established high-octane components. It also suggests new candidates, one of which we experimentally investigate and use to illustrate the need for further auto-ignition training data.

Multivariate Probabilistic Forecasting of Intraday Electricity Prices using Normalizing Flows

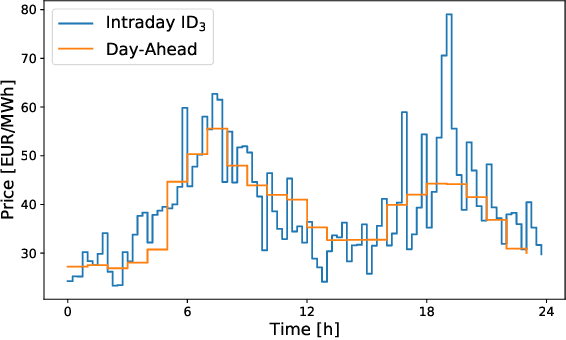
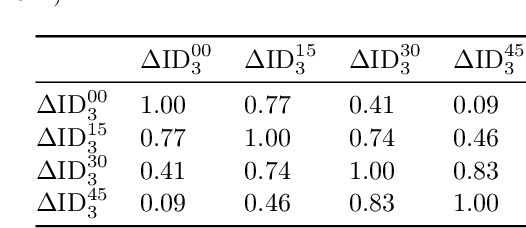
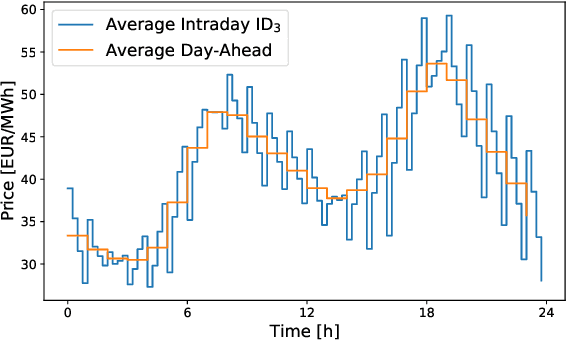
Electricity is traded on various markets with different time horizons and regulations. Short-term trading becomes increasingly important due to higher penetration of renewables. In Germany, the intraday electricity price typically fluctuates around the day-ahead price of the EPEX spot markets in a distinct hourly pattern. This work proposes a probabilistic modeling approach that models the intraday price difference to the day-ahead contracts. The model captures the emerging hourly pattern by considering the four 15 min intervals in each day-ahead price interval as a four-dimensional joint distribution. The resulting nontrivial, multivariate price difference distribution is learned using a normalizing flow, i.e., a deep generative model that combines conditional multivariate density estimation and probabilistic regression. The normalizing flow is compared to a selection of historical data, a Gaussian copula, and a Gaussian regression model. Among the different models, the normalizing flow identifies the trends most accurately and has the narrowest prediction intervals. Notably, the normalizing flow is the only approach that identifies rare price peaks. Finally, this work discusses the influence of different external impact factors and finds that, individually, most of these factors have negligible impact. Only the immediate history of the price difference realization and the combination of all input factors lead to notable improvements in the forecasts.