Data-Driven Model Reduction and Nonlinear Model Predictive Control of an Air Separation Unit by Applied Koopman Theory

Achieving real-time capability is an essential prerequisite for the industrial implementation of nonlinear model predictive control (NMPC). Data-driven model reduction offers a way to obtain low-order control models from complex digital twins. In particular, data-driven approaches require little expert knowledge of the particular process and its model, and provide reduced models of a well-defined generic structure. Herein, we apply our recently proposed data-driven reduction strategy based on Koopman theory [Schulze et al. (2022), Comput. Chem. Eng.] to generate a low-order control model of an air separation unit (ASU). The reduced Koopman model combines autoencoders and linear latent dynamics and is constructed using machine learning. Further, we present an NMPC implementation that uses derivative computation tailored to the fixed block structure of reduced Koopman models. Our reduction approach with tailored NMPC implementation enables real-time NMPC of an ASU at an average CPU time decrease by 98 %.

A Recursively Recurrent Neural Network (R2N2) Architecture for Learning Iterative Algorithms

Meta-learning of numerical algorithms for a given task consist of the data-driven identification and adaptation of an algorithmic structure and the associated hyperparameters. To limit the complexity of the meta-learning problem, neural architectures with a certain inductive bias towards favorable algorithmic structures can, and should, be used. We generalize our previously introduced Runge-Kutta neural network to a recursively recurrent neural network (R2N2) superstructure for the design of customized iterative algorithms. In contrast to off-the-shelf deep learning approaches, it features a distinct division into modules for generation of information and for the subsequent assembly of this information towards a solution. Local information in the form of a subspace is generated by subordinate, inner, iterations of recurrent function evaluations starting at the current outer iterate. The update to the next outer iterate is computed as a linear combination of these evaluations, reducing the residual in this space, and constitutes the output of the network. We demonstrate that regular training of the weight parameters inside the proposed superstructure on input/output data of various computational problem classes yields iterations similar to Krylov solvers for linear equation systems, Newton-Krylov solvers for nonlinear equation systems, and Runge-Kutta integrators for ordinary differential equations. Due to its modularity, the superstructure can be readily extended with functionalities needed to represent more general classes of iterative algorithms traditionally based on Taylor series expansions.

Hearts Gym: Learning Reinforcement Learning as a Team Event

Amidst the COVID-19 pandemic, the authors of this paper organized a Reinforcement Learning (RL) course for a graduate school in the field of data science. We describe the strategy and materials for creating an exciting learning experience despite the ubiquitous Zoom fatigue and evaluate the course qualitatively. The key organizational features are a focus on a competitive hands-on setting in teams, supported by a minimum of lectures providing the essential background on RL. The practical part of the course revolved around Hearts Gym, an RL environment for the card game Hearts that we developed as an entry-level tutorial to RL. Participants were tasked with training agents to explore reward shaping and other RL hyperparameters. For a final evaluation, the agents of the participants competed against each other.

Personalized Algorithm Generation: A Case Study in Meta-Learning ODE Integrators

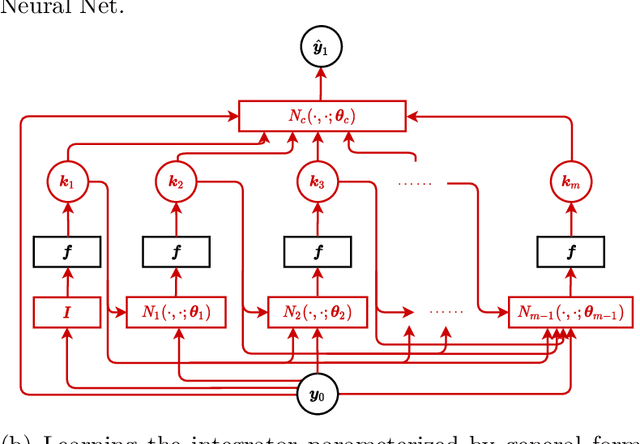
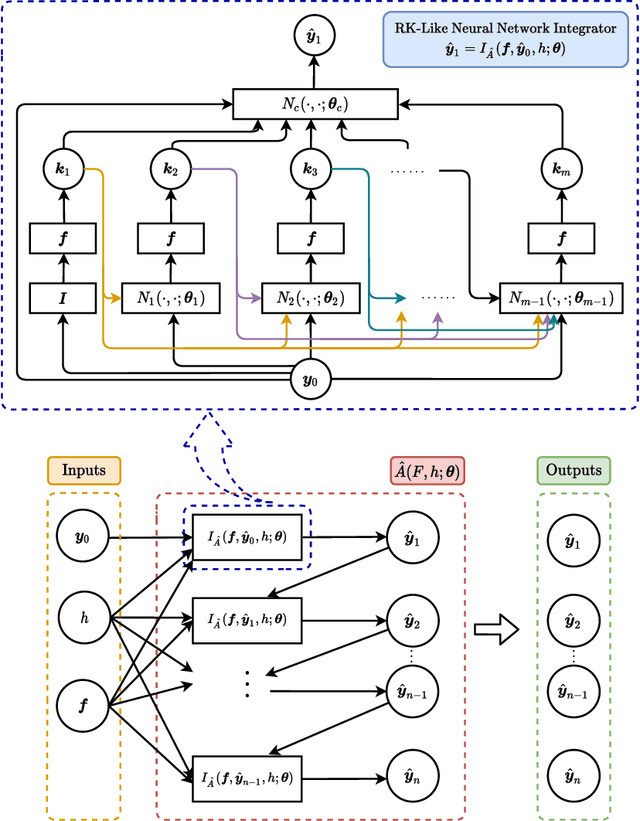
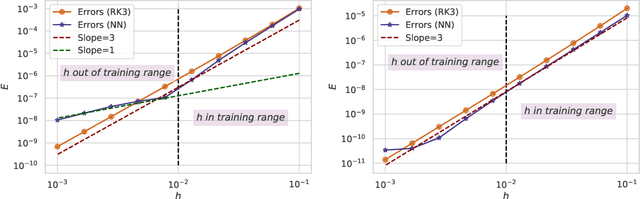
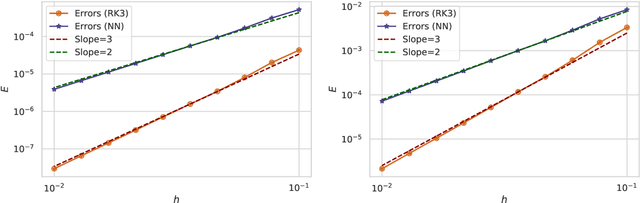
We study the meta-learning of numerical algorithms for scientific computing, which combines the mathematically driven, handcrafted design of general algorithm structure with a data-driven adaptation to specific classes of tasks. This represents a departure from the classical approaches in numerical analysis, which typically do not feature such learning-based adaptations. As a case study, we develop a machine learning approach that automatically learns effective solvers for initial value problems in the form of ordinary differential equations (ODEs), based on the Runge-Kutta (RK) integrator architecture. By combining neural network approximations and meta-learning, we show that we can obtain high-order integrators for targeted families of differential equations without the need for computing integrator coefficients by hand. Moreover, we demonstrate that in certain cases we can obtain superior performance to classical RK methods. This can be attributed to certain properties of the ODE families being identified and exploited by the approach. Overall, this work demonstrates an effective, learning-based approach to the design of algorithms for the numerical solution of differential equations, an approach that can be readily extended to other numerical tasks.