Nonlinear Model Order Reduction of Dynamical Systems in Process Engineering: Review and Comparison

Computationally cheap yet accurate enough dynamical models are vital for real-time capable nonlinear optimization and model-based control. When given a computationally expensive high-order prediction model, a reduction to a lower-order simplified model can enable such real-time applications. Herein, we review state-of-the-art nonlinear model order reduction methods and provide a theoretical comparison of method properties. Additionally, we discuss both general-purpose methods and tailored approaches for (chemical) process systems and we identify similarities and differences between these methods. As manifold-Galerkin approaches currently do not account for inputs in the construction of the reduced state subspace, we extend these methods to dynamical systems with inputs. In a comparative case study, we apply eight established model order reduction methods to an air separation process model: POD-Galerkin, nonlinear-POD-Galerkin, manifold-Galerkin, dynamic mode decomposition, Koopman theory, manifold learning with latent predictor, compartment modeling, and model aggregation. Herein, we do not investigate hyperreduction (reduction of FLOPS). Based on our findings, we discuss strengths and weaknesses of the model order reduction methods.

Deterministic Global Optimization of the Acquisition Function in Bayesian Optimization: To Do or Not To Do?

Bayesian Optimization (BO) with Gaussian Processes relies on optimizing an acquisition function to determine sampling. We investigate the advantages and disadvantages of using a deterministic global solver (MAiNGO) compared to conventional local and stochastic global solvers (L-BFGS-B and multi-start, respectively) for the optimization of the acquisition function. For CPU efficiency, we set a time limit for MAiNGO, taking the best point as optimal. We perform repeated numerical experiments, initially using the Muller-Brown potential as a benchmark function, utilizing the lower confidence bound acquisition function; we further validate our findings with three alternative benchmark functions. Statistical analysis reveals that when the acquisition function is more exploitative (as opposed to exploratory), BO with MAiNGO converges in fewer iterations than with the local solvers. However, when the dataset lacks diversity, or when the acquisition function is overly exploitative, BO with MAiNGO, compared to the local solvers, is more likely to converge to a local rather than a global ly near-optimal solution of the black-box function. L-BFGS-B and multi-start mitigate this risk in BO by introducing stochasticity in the selection of the next sampling point, which enhances the exploration of uncharted regions in the search space and reduces dependence on acquisition function hyperparameters. Ultimately, suboptimal optimization of poorly chosen acquisition functions may be preferable to their optimal solution. When the acquisition function is more exploratory, BO with MAiNGO, multi-start, and L-BFGS-B achieve comparable probabilities of convergence to a globally near-optimal solution (although BO with MAiNGO may require more iterations to converge under these conditions).

Predicting the Temperature-Dependent CMC of Surfactant Mixtures with Graph Neural Networks

Surfactants are key ingredients in foaming and cleansing products across various industries such as personal and home care, industrial cleaning, and more, with the critical micelle concentration (CMC) being of major interest. Predictive models for CMC of pure surfactants have been developed based on recent ML methods, however, in practice surfactant mixtures are typically used due to to performance, environmental, and cost reasons. This requires accounting for synergistic/antagonistic interactions between surfactants; however, predictive ML models for a wide spectrum of mixtures are missing so far. Herein, we develop a graph neural network (GNN) framework for surfactant mixtures to predict the temperature-dependent CMC. We collect data for 108 surfactant binary mixtures, to which we add data for pure species from our previous work [Brozos et al. (2024), J. Chem. Theory Comput.]. We then develop and train GNNs and evaluate their accuracy across different prediction test scenarios for binary mixtures relevant to practical applications. The final GNN models demonstrate very high predictive performance when interpolating between different mixture compositions and for new binary mixtures with known species. Extrapolation to binary surfactant mixtures where either one or both surfactant species are not seen before, yields accurate results for the majority of surfactant systems. We further find superior accuracy of the GNN over a semi-empirical model based on activity coefficients, which has been widely used to date. We then explore if GNN models trained solely on binary mixture and pure species data can also accurately predict the CMCs of ternary mixtures. Finally, we experimentally measure the CMC of 4 commercial surfactants that contain up to four species and industrial relevant mixtures and find a very good agreement between measured and predicted CMC values.

GraphXForm: Graph transformer for computer-aided molecular design with application to extraction

Generative deep learning has become pivotal in molecular design for drug discovery and materials science. A widely used paradigm is to pretrain neural networks on string representations of molecules and fine-tune them using reinforcement learning on specific objectives. However, string-based models face challenges in ensuring chemical validity and enforcing structural constraints like the presence of specific substructures. We propose to instead combine graph-based molecular representations, which can naturally ensure chemical validity, with transformer architectures, which are highly expressive and capable of modeling long-range dependencies between atoms. Our approach iteratively modifies a molecular graph by adding atoms and bonds, which ensures chemical validity and facilitates the incorporation of structural constraints. We present GraphXForm, a decoder-only graph transformer architecture, which is pretrained on existing compounds and then fine-tuned using a new training algorithm that combines elements of the deep cross-entropy method with self-improvement learning from language modeling, allowing stable fine-tuning of deep transformers with many layers. We evaluate GraphXForm on two solvent design tasks for liquid-liquid extraction, showing that it outperforms four state-of-the-art molecular design techniques, while it can flexibly enforce structural constraints or initiate the design from existing molecular structures.

Physics-Informed Neural Networks for Dynamic Process Operations with Limited Physical Knowledge and Data

In chemical engineering, process data is often expensive to acquire, and complex phenomena are difficult to model rigorously, rendering both entirely data-driven and purely mechanistic modeling approaches impractical. We explore using physics-informed neural networks (PINNs) for modeling dynamic processes governed by differential-algebraic equation systems when process data is scarce and complete mechanistic knowledge is missing. In particular, we focus on estimating states for which neither direct observational data nor constitutive equations are available. For demonstration purposes, we study a continuously stirred tank reactor and a liquid-liquid separator. We find that PINNs can infer unmeasured states with reasonable accuracy, and they generalize better in low-data scenarios than purely data-driven models. We thus show that PINNs, similar to hybrid mechanistic/data-driven models, are capable of modeling processes when relatively few experimental data and only partially known mechanistic descriptions are available, and conclude that they constitute a promising avenue that warrants further investigation.

Task-optimal data-driven surrogate models for eNMPC via differentiable simulation and optimization

We present a method for end-to-end learning of Koopman surrogate models for optimal performance in control. In contrast to previous contributions that employ standard reinforcement learning (RL) algorithms, we use a training algorithm that exploits the potential differentiability of environments based on mechanistic simulation models. We evaluate the performance of our method by comparing it to that of other controller type and training algorithm combinations on a literature known eNMPC case study. Our method exhibits superior performance on this problem, thereby constituting a promising avenue towards more capable controllers that employ dynamic surrogate models.

Nonlinear Manifold Learning Determines Microgel Size from Raman Spectroscopy

Polymer particle size constitutes a crucial characteristic of product quality in polymerization. Raman spectroscopy is an established and reliable process analytical technology for in-line concentration monitoring. Recent approaches and some theoretical considerations show a correlation between Raman signals and particle sizes but do not determine polymer size from Raman spectroscopic measurements accurately and reliably. With this in mind, we propose three alternative machine learning workflows to perform this task, all involving diffusion maps, a nonlinear manifold learning technique for dimensionality reduction: (i) directly from diffusion maps, (ii) alternating diffusion maps, and (iii) conformal autoencoder neural networks. We apply the workflows to a data set of Raman spectra with associated size measured via dynamic light scattering of 47 microgel (cross-linked polymer) samples in a diameter range of 208nm to 483 nm. The conformal autoencoders substantially outperform state-of-the-art methods and results for the first time in a promising prediction of polymer size from Raman spectra.

Predicting the Temperature Dependence of Surfactant CMCs Using Graph Neural Networks

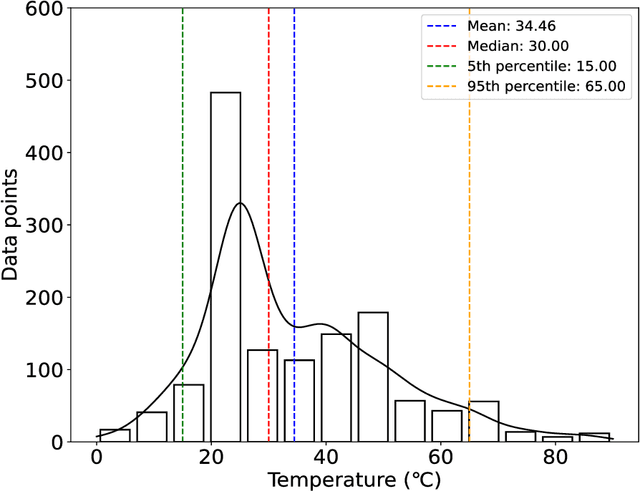
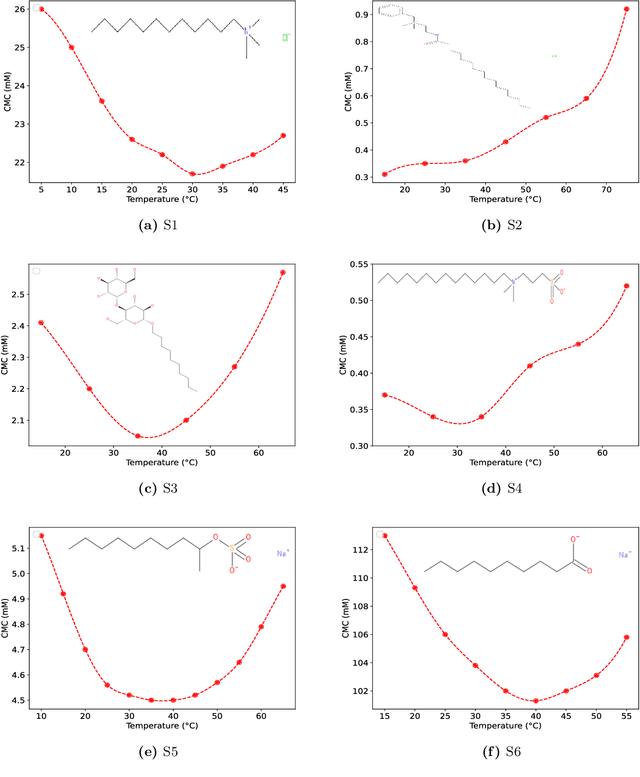
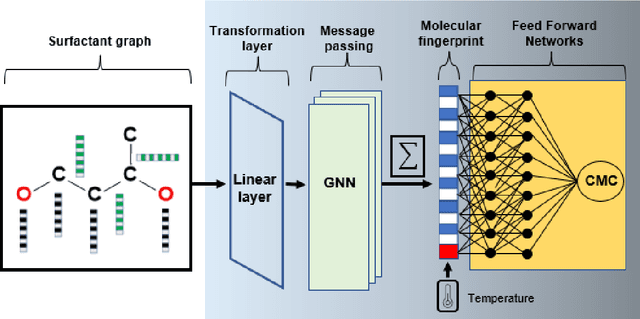
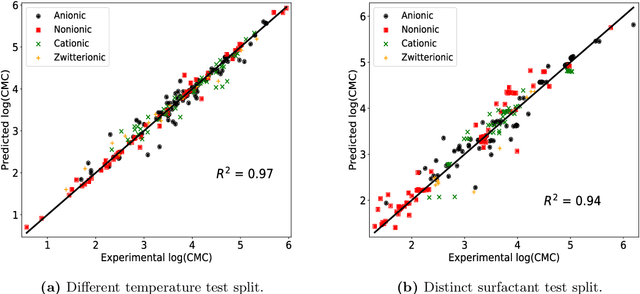
The critical micelle concentration (CMC) of surfactant molecules is an essential property for surfactant applications in industry. Recently, classical QSPR and Graph Neural Networks (GNNs), a deep learning technique, have been successfully applied to predict the CMC of surfactants at room temperature. However, these models have not yet considered the temperature dependency of the CMC, which is highly relevant for practical applications. We herein develop a GNN model for temperature-dependent CMC prediction of surfactants. We collect about 1400 data points from public sources for all surfactant classes, i.e., ionic, nonionic, and zwitterionic, at multiple temperatures. We test the predictive quality of the model for following scenarios: i) when CMC data for surfactants are present in the training of the model in at least one different temperature, and ii) CMC data for surfactants are not present in the training, i.e., generalizing to unseen surfactants. In both test scenarios, our model exhibits a high predictive performance of R$^2 \geq $ 0.94 on test data. We also find that the model performance varies by surfactant class. Finally, we evaluate the model for sugar-based surfactants with complex molecular structures, as these represent a more sustainable alternative to synthetic surfactants and are therefore of great interest for future applications in the personal and home care industries.

Data-driven Nonlinear Model Reduction using Koopman Theory: Integrated Control Form and NMPC Case Study

We use Koopman theory for data-driven model reduction of nonlinear dynamical systems with controls. We propose generic model structures combining delay-coordinate encoding of measurements and full-state decoding to integrate reduced Koopman modeling and state estimation. We present a deep-learning approach to train the proposed models. A case study demonstrates that our approach provides accurate control models and enables real-time capable nonlinear model predictive control of a high-purity cryogenic distillation column.

Graph Neural Networks for Surfactant Multi-Property Prediction

Surfactants are of high importance in different industrial sectors such as cosmetics, detergents, oil recovery and drug delivery systems. Therefore, many quantitative structure-property relationship (QSPR) models have been developed for surfactants. Each predictive model typically focuses on one surfactant class, mostly nonionics. Graph Neural Networks (GNNs) have exhibited a great predictive performance for property prediction of ionic liquids, polymers and drugs in general. Specifically for surfactants, GNNs can successfully predict critical micelle concentration (CMC), a key surfactant property associated with micellization. A key factor in the predictive ability of QSPR and GNN models is the data available for training. Based on extensive literature search, we create the largest available CMC database with 429 molecules and the first large data collection for surface excess concentration ($\Gamma$$_{m}$), another surfactant property associated with foaming, with 164 molecules. Then, we develop GNN models to predict the CMC and $\Gamma$$_{m}$ and we explore different learning approaches, i.e., single- and multi-task learning, as well as different training strategies, namely ensemble and transfer learning. We find that a multi-task GNN with ensemble learning trained on all $\Gamma$$_{m}$ and CMC data performs best. Finally, we test the ability of our CMC model to generalize on industrial grade pure component surfactants. The GNN yields highly accurate predictions for CMC, showing great potential for future industrial applications.