Model-Free Stochastic Process Modeling and Optimization using Normalizing Flows

Real-world chemical processes often exhibit stochastic dynamics with non-trivial correlations and state-dependent fluctuations. However, most process models simply add stationary noise terms to a deterministic prediction, which can lead to inaccurate predictions. This work proposes using conditional normalizing flows as discrete-time models (DTMs) to learn the stochastic dynamics of chemical processes. Normalizing flows learn an explicit expression of the system states' probability density function (PDF) given prior states and control inputs. The resulting model naturally allows for formulating stochastic and probabilistic setpoint-tracking objectives and chance constraints. In applications to a continuous reactor and a reactor cascade, the normalizing flow yields stable simulations over long time horizons and high-quality results in stochastic and probabilistic MPC formulation for open-loop control. Furthermore, a chance-constrained optimization finds reliable startup controls for the reactor cascade with stochastic reactions. In conclusion, the conditional normalizing flow presents an excellent choice for modeling nonlinear stochastic dynamics.

Multivariate Scenario Generation of Day-Ahead Electricity Prices using Normalizing Flows

Trading on electricity markets requires accurate information about the realization of electricity prices and the uncertainty attached to the predictions. We present a probabilistic forecasting approach for day-ahead electricity prices using the fully data-driven deep generative model called normalizing flows. Our modeling approach generates full-day scenarios of day-ahead electricity prices based on conditional features such as residual load forecasts. Furthermore, we propose extended feature sets of prior realizations and a periodic retraining scheme that allows the normalizing flow to adapt to the changing conditions of modern electricity markets. In particular, we investigate the impact of the energy crisis ensuing from the Russian invasion of Ukraine. Our results highlight that the normalizing flow generates high-quality scenarios that reproduce the true price distribution and yield highly accurate forecasts. Additionally, our analysis highlights how our improvements towards adaptations in changing regimes allow the normalizing flow to adapt to changing market conditions and enables continued sampling of high-quality day-ahead price scenarios.

Multivariate Probabilistic Forecasting of Intraday Electricity Prices using Normalizing Flows

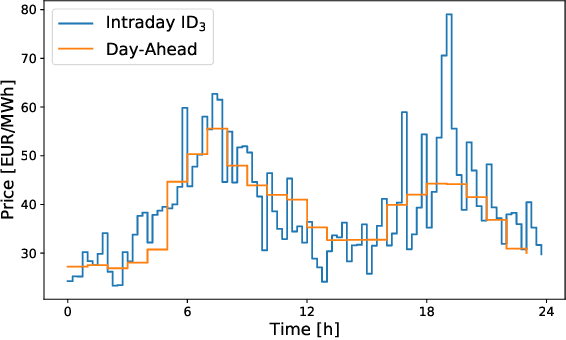
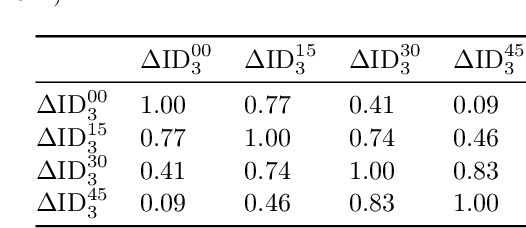
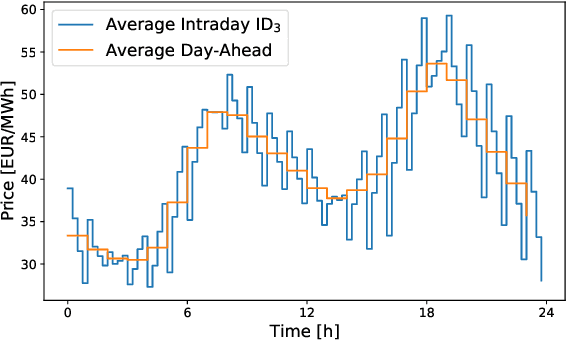
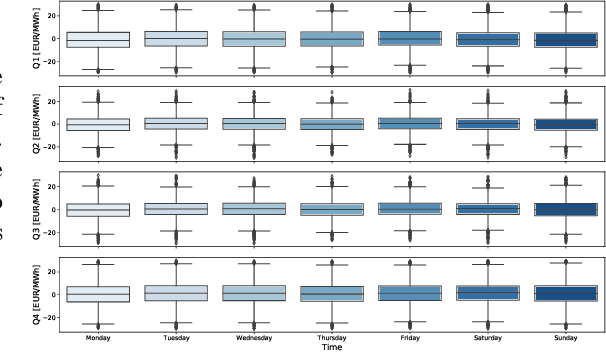
Electricity is traded on various markets with different time horizons and regulations. Short-term trading becomes increasingly important due to higher penetration of renewables. In Germany, the intraday electricity price typically fluctuates around the day-ahead price of the EPEX spot markets in a distinct hourly pattern. This work proposes a probabilistic modeling approach that models the intraday price difference to the day-ahead contracts. The model captures the emerging hourly pattern by considering the four 15 min intervals in each day-ahead price interval as a four-dimensional joint distribution. The resulting nontrivial, multivariate price difference distribution is learned using a normalizing flow, i.e., a deep generative model that combines conditional multivariate density estimation and probabilistic regression. The normalizing flow is compared to a selection of historical data, a Gaussian copula, and a Gaussian regression model. Among the different models, the normalizing flow identifies the trends most accurately and has the narrowest prediction intervals. Notably, the normalizing flow is the only approach that identifies rare price peaks. Finally, this work discusses the influence of different external impact factors and finds that, individually, most of these factors have negligible impact. Only the immediate history of the price difference realization and the combination of all input factors lead to notable improvements in the forecasts.

Normalizing Flow-based Day-Ahead Wind Power Scenario Generation for Profitable and Reliable Delivery Commitments by Wind Farm Operators

We present a specialized scenario generation method that utilizes forecast information to generate scenarios for the particular usage in day-ahead scheduling problems. In particular, we use normalizing flows to generate wind power generation scenarios by sampling from a conditional distribution that uses day-ahead wind speed forecasts to tailor the scenarios to the specific day. We apply the generated scenarios in a simple stochastic day-ahead bidding problem of a wind electricity producer and run a statistical analysis focusing on whether the scenarios yield profitable and reliable decisions. Compared to conditional scenarios generated from Gaussian copulas and Wasserstein-generative adversarial networks, the normalizing flow scenarios identify the daily trends more accurately and with a lower spread while maintaining a diverse variety. In the stochastic day-ahead bidding problem, the conditional scenarios from all methods lead to significantly more profitable and reliable results compared to an unconditional selection of historical scenarios. The obtained profits using the normalizing flow scenarios are consistently closest to the perfect foresight solution, in particular, for small sets of only five scenarios.

Nonlinear Isometric Manifold Learning for Injective Normalizing Flows

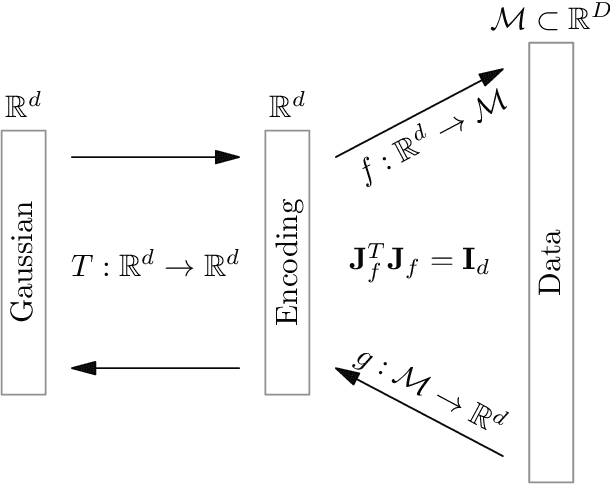
To model manifold data using normalizing flows, we propose to employ the isometric autoencoder to design nonlinear encodings with explicit inverses. The isometry allows us to separate manifold learning and density estimation and train both parts to high accuracy. Applied to the MNIST data set, the combined approach generates high-quality images.

Validation Methods for Energy Time Series Scenarios from Deep Generative Models

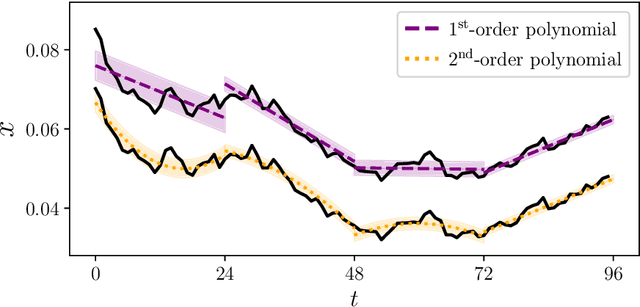
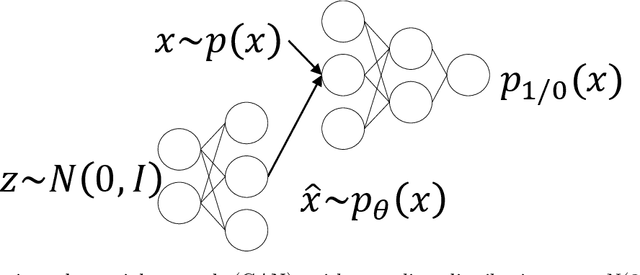
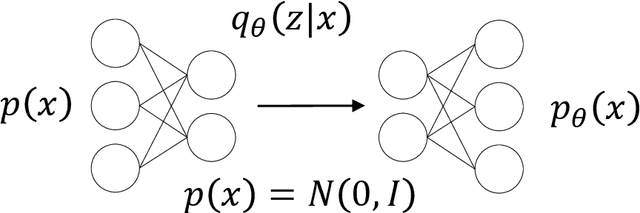
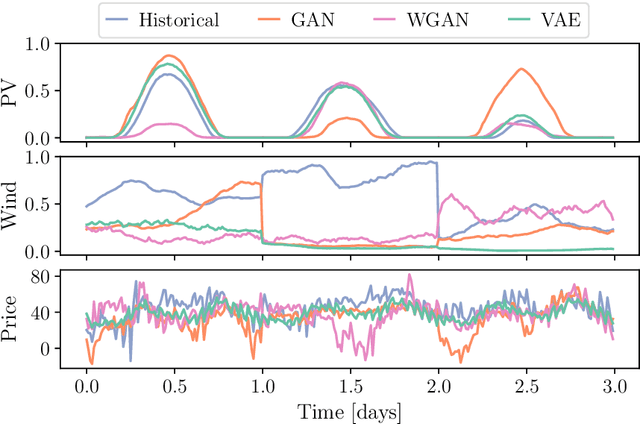
The design and operation of modern energy systems are heavily influenced by time-dependent and uncertain parameters, e.g., renewable electricity generation, load-demand, and electricity prices. These are typically represented by a set of discrete realizations known as scenarios. A popular scenario generation approach uses deep generative models (DGM) that allow scenario generation without prior assumptions about the data distribution. However, the validation of generated scenarios is difficult, and a comprehensive discussion about appropriate validation methods is currently lacking. To start this discussion, we provide a critical assessment of the currently used validation methods in the energy scenario generation literature. In particular, we assess validation methods based on probability density, auto-correlation, and power spectral density. Furthermore, we propose using the multifractal detrended fluctuation analysis (MFDFA) as an additional validation method for non-trivial features like peaks, bursts, and plateaus. As representative examples, we train generative adversarial networks (GANs), Wasserstein GANs (WGANs), and variational autoencoders (VAEs) on two renewable power generation time series (photovoltaic and wind from Germany in 2013 to 2015) and an intra-day electricity price time series form the European Energy Exchange in 2017 to 2019. We apply the four validation methods to both the historical and the generated data and discuss the interpretation of validation results as well as common mistakes, pitfalls, and limitations of the validation methods. Our assessment shows that no single method sufficiently characterizes a scenario but ideally validation should include multiple methods and be interpreted carefully in the context of scenarios over short time periods.

Principal Component Density Estimation for Scenario Generation Using Normalizing Flows

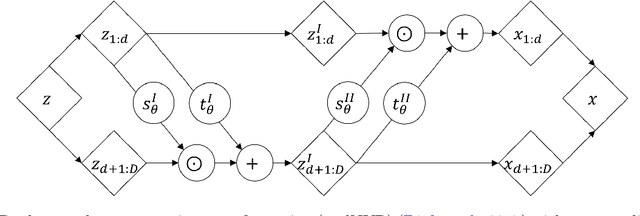
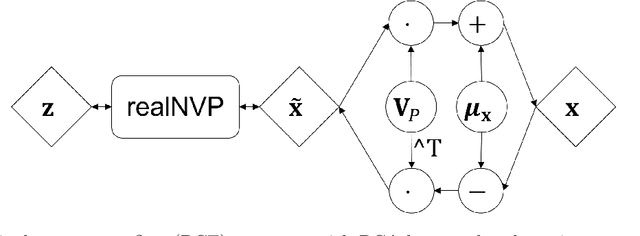
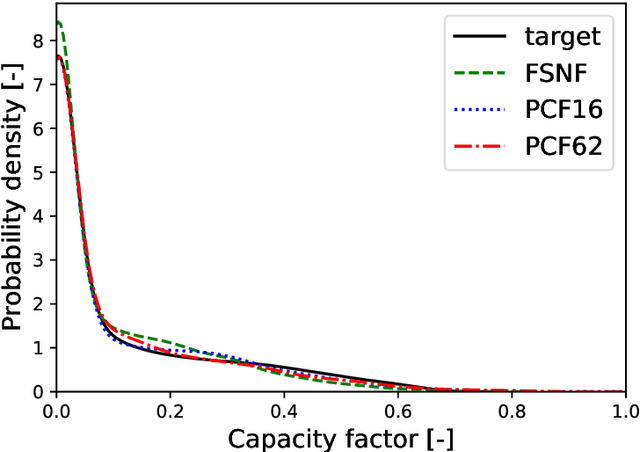
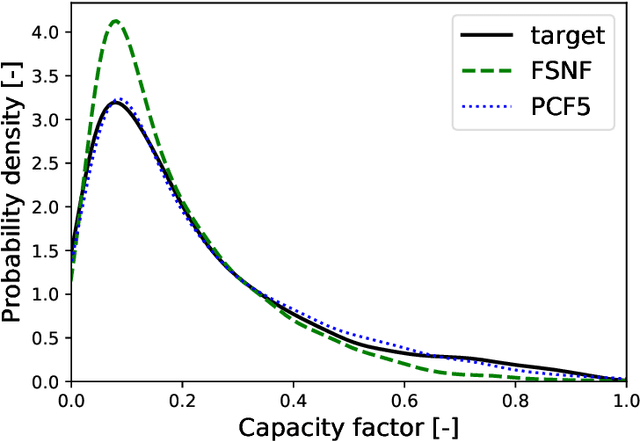
Neural networks-based learning of the distribution of non-dispatchable renewable electricity generation from sources such as photovoltaics (PV) and wind as well as load demands has recently gained attention. Normalizing flow density models have performed particularly well in this task due to the training through direct log-likelihood maximization. However, research from the field of image generation has shown that standard normalizing flows can only learn smeared-out versions of manifold distributions and can result in the generation of noisy data. To avoid the generation of time series data with unrealistic noise, we propose a dimensionality-reducing flow layer based on the linear principal component analysis (PCA) that sets up the normalizing flow in a lower-dimensional space. We train the resulting principal component flow (PCF) on data of PV and wind power generation as well as load demand in Germany in the years 2013 to 2015. The results of this investigation show that the PCF preserves critical features of the original distributions, such as the probability density and frequency behavior of the time series. The application of the PCF is, however, not limited to renewable power generation but rather extends to any data set, time series, or otherwise, which can be efficiently reduced using PCA.