Stochastic differential equations for performance analysis of wireless communication systems

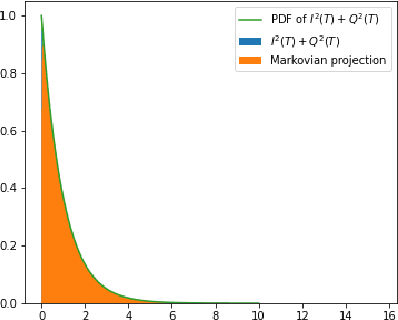
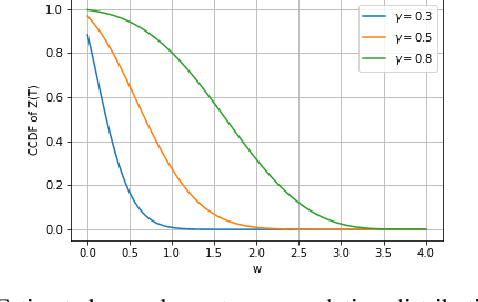
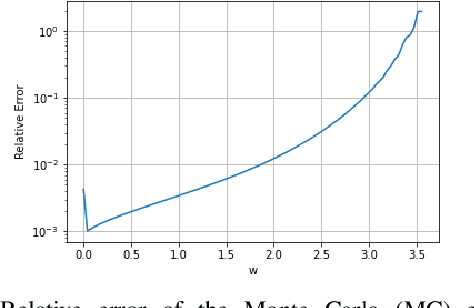
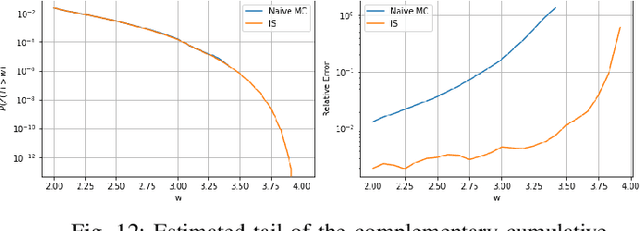
This paper addresses the difficulty of characterizing the time-varying nature of fading channels. The current time-invariant models often fall short of capturing and tracking these dynamic characteristics. To overcome this limitation, we explore using of stochastic differential equations (SDEs) and Markovian projection to model signal envelope variations, considering scenarios involving Rayleigh, Rice, and Hoyt distributions. Furthermore, it is of practical interest to study the performance of channels modeled by SDEs. In this work, we investigate the fade duration metric, representing the time during which the signal remains below a specified threshold within a fixed time interval. We estimate the complementary cumulative distribution function (CCDF) of the fade duration using Monte Carlo simulations, and analyze the influence of system parameters on its behavior. Finally, we leverage importance sampling, a known variance-reduction technique, to estimate the tail of the CCDF efficiently.

Residual Multi-Fidelity Neural Network Computing

In this work, we consider the general problem of constructing a neural network surrogate model using multi-fidelity information. Given an inexpensive low-fidelity and an expensive high-fidelity computational model, we present a residual multi-fidelity computational framework that formulates the correlation between models as a residual function, a possibly non-linear mapping between 1) the shared input space of the models together with the low-fidelity model output and 2) the discrepancy between the two model outputs. To accomplish this, we train two neural networks to work in concert. The first network learns the residual function on a small set of high-fidelity and low-fidelity data. Once trained, this network is used to generate additional synthetic high-fidelity data, which is used in the training of a second network. This second network, once trained, acts as our surrogate for the high-fidelity quantity of interest. We present three numerical examples to demonstrate the power of the proposed framework. In particular, we show that dramatic savings in computational cost may be achieved when the output predictions are desired to be accurate within small tolerances.

Physics-informed Spectral Learning: the Discrete Helmholtz--Hodge Decomposition

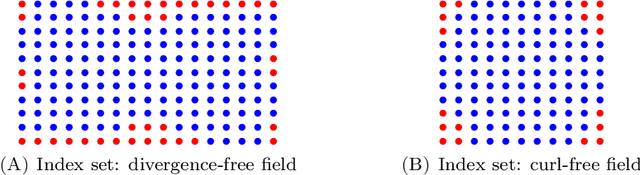
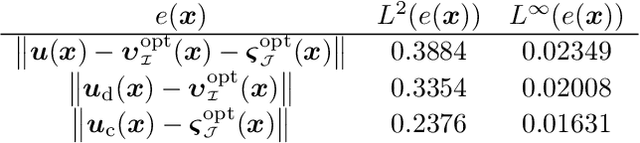
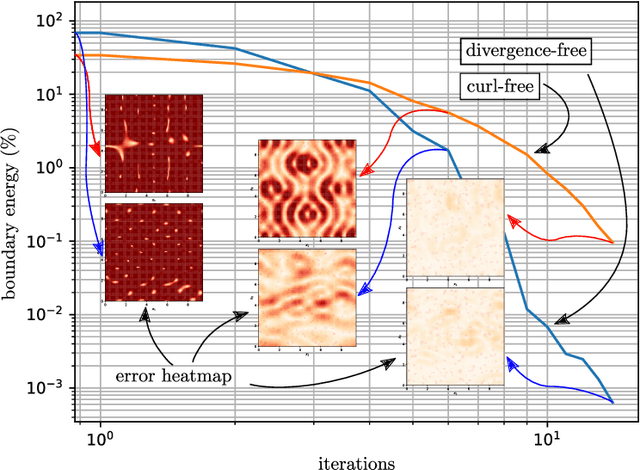
In this work, we further develop the Physics-informed Spectral Learning (PiSL) by Espath et al. \cite{Esp21} based on a discrete $L^2$ projection to solve the discrete Hodge--Helmholtz decomposition from sparse data. Within this physics-informed statistical learning framework, we adaptively build a sparse set of Fourier basis functions with corresponding coefficients by solving a sequence of minimization problems where the set of basis functions is augmented greedily at each optimization problem. Moreover, our PiSL computational framework enjoys spectral (exponential) convergence. We regularize the minimization problems with the seminorm of the fractional Sobolev space in a Tikhonov fashion. In the Fourier setting, the divergence- and curl-free constraints become a finite set of linear algebraic equations. The proposed computational framework combines supervised and unsupervised learning techniques in that we use data concomitantly with the projection onto divergence- and curl-free spaces. We assess the capabilities of our method in various numerical examples including the `Storm of the Century' with satellite data from 1993.

Principal Component Density Estimation for Scenario Generation Using Normalizing Flows

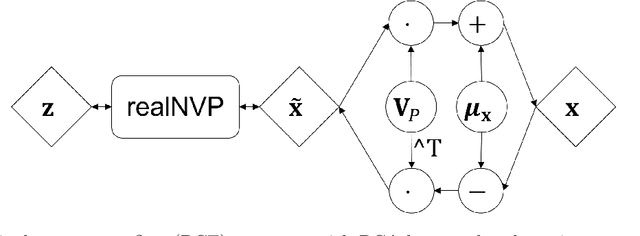
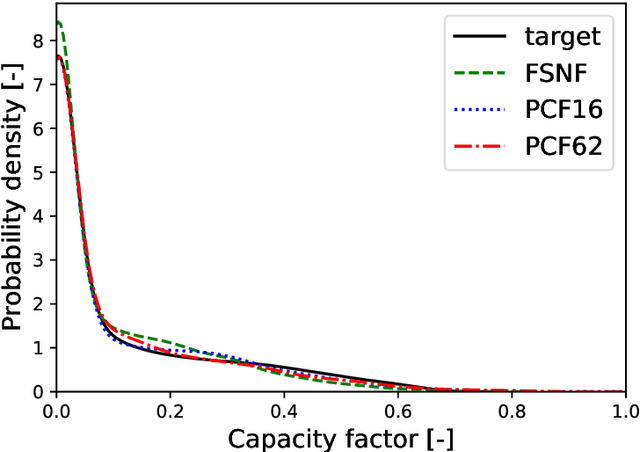
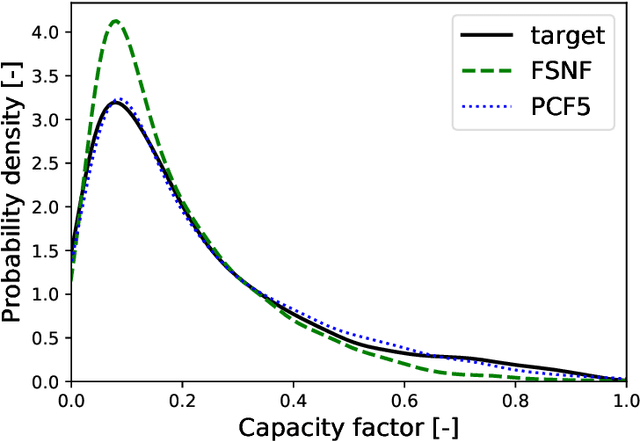
Neural networks-based learning of the distribution of non-dispatchable renewable electricity generation from sources such as photovoltaics (PV) and wind as well as load demands has recently gained attention. Normalizing flow density models have performed particularly well in this task due to the training through direct log-likelihood maximization. However, research from the field of image generation has shown that standard normalizing flows can only learn smeared-out versions of manifold distributions and can result in the generation of noisy data. To avoid the generation of time series data with unrealistic noise, we propose a dimensionality-reducing flow layer based on the linear principal component analysis (PCA) that sets up the normalizing flow in a lower-dimensional space. We train the resulting principal component flow (PCF) on data of PV and wind power generation as well as load demand in Germany in the years 2013 to 2015. The results of this investigation show that the PCF preserves critical features of the original distributions, such as the probability density and frequency behavior of the time series. The application of the PCF is, however, not limited to renewable power generation but rather extends to any data set, time series, or otherwise, which can be efficiently reduced using PCA.

Mean-Field Learning: a Survey

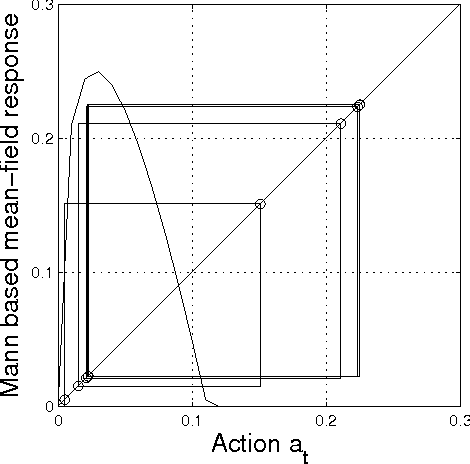
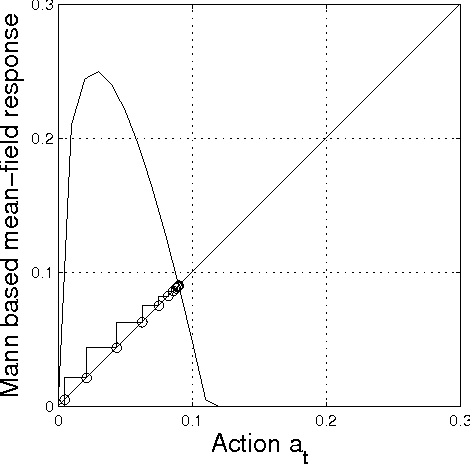
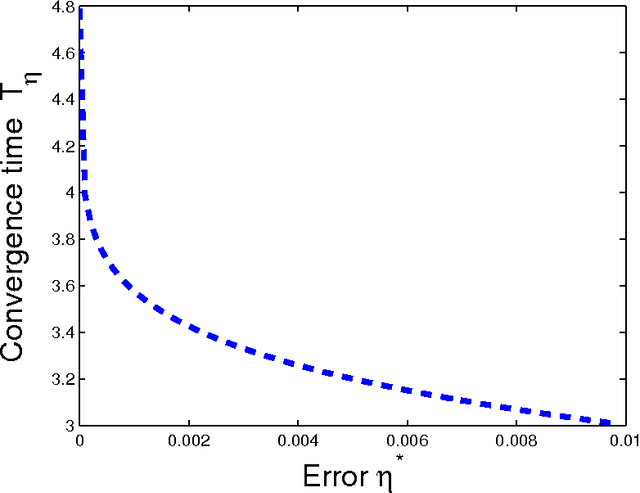
In this paper we study iterative procedures for stationary equilibria in games with large number of players. Most of learning algorithms for games with continuous action spaces are limited to strict contraction best reply maps in which the Banach-Picard iteration converges with geometrical convergence rate. When the best reply map is not a contraction, Ishikawa-based learning is proposed. The algorithm is shown to behave well for Lipschitz continuous and pseudo-contractive maps. However, the convergence rate is still unsatisfactory. Several acceleration techniques are presented. We explain how cognitive users can improve the convergence rate based only on few number of measurements. The methodology provides nice properties in mean field games where the payoff function depends only on own-action and the mean of the mean-field (first moment mean-field games). A learning framework that exploits the structure of such games, called, mean-field learning, is proposed. The proposed mean-field learning framework is suitable not only for games but also for non-convex global optimization problems. Then, we introduce mean-field learning without feedback and examine the convergence to equilibria in beauty contest games, which have interesting applications in financial markets. Finally, we provide a fully distributed mean-field learning and its speedup versions for satisfactory solution in wireless networks. We illustrate the convergence rate improvement with numerical examples.