Deep Learning without Global Optimization by Random Fourier Neural Networks

We introduce a new training algorithm for variety of deep neural networks that utilize random complex exponential activation functions. Our approach employs a Markov Chain Monte Carlo sampling procedure to iteratively train network layers, avoiding global and gradient-based optimization while maintaining error control. It consistently attains the theoretical approximation rate for residual networks with complex exponential activation functions, determined by network complexity. Additionally, it enables efficient learning of multiscale and high-frequency features, producing interpretable parameter distributions. Despite using sinusoidal basis functions, we do not observe Gibbs phenomena in approximating discontinuous target functions.

Approximation Error and Complexity Bounds for ReLU Networks on Low-Regular Function Spaces

In this work, we consider the approximation of a large class of bounded functions, with minimal regularity assumptions, by ReLU neural networks. We show that the approximation error can be bounded from above by a quantity proportional to the uniform norm of the target function and inversely proportional to the product of network width and depth. We inherit this approximation error bound from Fourier features residual networks, a type of neural network that uses complex exponential activation functions. Our proof is constructive and proceeds by conducting a careful complexity analysis associated with the approximation of a Fourier features residual network by a ReLU network.

Residual Multi-Fidelity Neural Network Computing

In this work, we consider the general problem of constructing a neural network surrogate model using multi-fidelity information. Given an inexpensive low-fidelity and an expensive high-fidelity computational model, we present a residual multi-fidelity computational framework that formulates the correlation between models as a residual function, a possibly non-linear mapping between 1) the shared input space of the models together with the low-fidelity model output and 2) the discrepancy between the two model outputs. To accomplish this, we train two neural networks to work in concert. The first network learns the residual function on a small set of high-fidelity and low-fidelity data. Once trained, this network is used to generate additional synthetic high-fidelity data, which is used in the training of a second network. This second network, once trained, acts as our surrogate for the high-fidelity quantity of interest. We present three numerical examples to demonstrate the power of the proposed framework. In particular, we show that dramatic savings in computational cost may be achieved when the output predictions are desired to be accurate within small tolerances.

Approximation Power of Deep Neural Networks: an explanatory mathematical survey

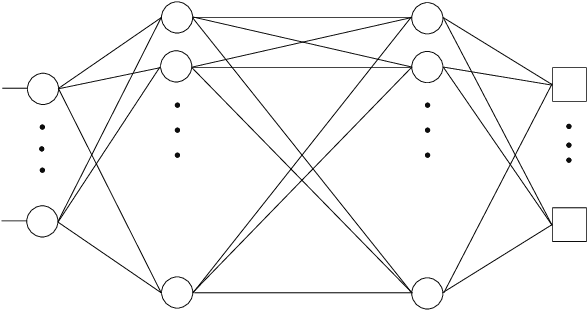
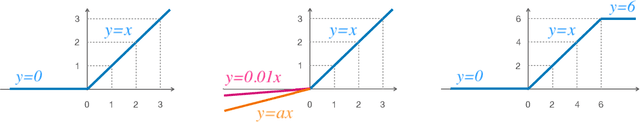
The goal of this survey is to present an explanatory review of the approximation properties of deep neural networks. Specifically, we aim at understanding how and why deep neural networks outperform other classical linear and nonlinear approximation methods. This survey consists of three chapters. In Chapter 1 we review the key ideas and concepts underlying deep networks and their compositional nonlinear structure. We formalize the neural network problem by formulating it as an optimization problem when solving regression and classification problems. We briefly discuss the stochastic gradient descent algorithm and the back-propagation formulas used in solving the optimization problem and address a few issues related to the performance of neural networks, including the choice of activation functions, cost functions, overfitting issues, and regularization. In Chapter 2 we shift our focus to the approximation theory of neural networks. We start with an introduction to the concept of density in polynomial approximation and in particular study the Stone-Weierstrass theorem for real-valued continuous functions. Then, within the framework of linear approximation, we review a few classical results on the density and convergence rate of feedforward networks, followed by more recent developments on the complexity of deep networks in approximating Sobolev functions. In Chapter 3, utilizing nonlinear approximation theory, we further elaborate on the power of depth and approximation superiority of deep ReLU networks over other classical methods of nonlinear approximation.