NeurAM: nonlinear dimensionality reduction for uncertainty quantification through neural active manifolds

We present a new approach for nonlinear dimensionality reduction, specifically designed for computationally expensive mathematical models. We leverage autoencoders to discover a one-dimensional neural active manifold (NeurAM) capturing the model output variability, plus a simultaneously learnt surrogate model with inputs on this manifold. The proposed dimensionality reduction framework can then be applied to perform outer loop many-query tasks, like sensitivity analysis and uncertainty propagation. In particular, we prove, both theoretically under idealized conditions, and numerically in challenging test cases, how NeurAM can be used to obtain multifidelity sampling estimators with reduced variance by sampling the models on the discovered low-dimensional and shared manifold among models. Several numerical examples illustrate the main features of the proposed dimensionality reduction strategy, and highlight its advantages with respect to existing approaches in the literature.

Deep Learning without Global Optimization by Random Fourier Neural Networks

We introduce a new training algorithm for variety of deep neural networks that utilize random complex exponential activation functions. Our approach employs a Markov Chain Monte Carlo sampling procedure to iteratively train network layers, avoiding global and gradient-based optimization while maintaining error control. It consistently attains the theoretical approximation rate for residual networks with complex exponential activation functions, determined by network complexity. Additionally, it enables efficient learning of multiscale and high-frequency features, producing interpretable parameter distributions. Despite using sinusoidal basis functions, we do not observe Gibbs phenomena in approximating discontinuous target functions.

Approximation Error and Complexity Bounds for ReLU Networks on Low-Regular Function Spaces

In this work, we consider the approximation of a large class of bounded functions, with minimal regularity assumptions, by ReLU neural networks. We show that the approximation error can be bounded from above by a quantity proportional to the uniform norm of the target function and inversely proportional to the product of network width and depth. We inherit this approximation error bound from Fourier features residual networks, a type of neural network that uses complex exponential activation functions. Our proof is constructive and proceeds by conducting a careful complexity analysis associated with the approximation of a Fourier features residual network by a ReLU network.

Multifidelity data fusion in convolutional encoder/decoder networks

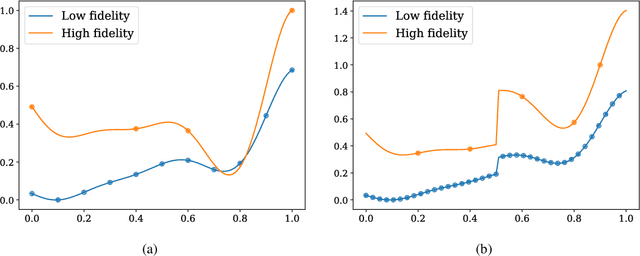
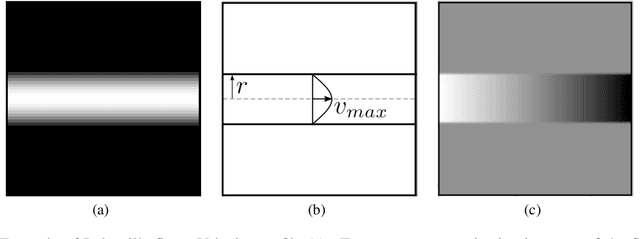
We analyze the regression accuracy of convolutional neural networks assembled from encoders, decoders and skip connections and trained with multifidelity data. Besides requiring significantly less trainable parameters than equivalent fully connected networks, encoder, decoder, encoder-decoder or decoder-encoder architectures can learn the mapping between inputs to outputs of arbitrary dimensionality. We demonstrate their accuracy when trained on a few high-fidelity and many low-fidelity data generated from models ranging from one-dimensional functions to Poisson equation solvers in two-dimensions. We finally discuss a number of implementation choices that improve the reliability of the uncertainty estimates generated by Monte Carlo DropBlocks, and compare uncertainty estimates among low-, high- and multifidelity approaches.

MFNets: Learning network representations for multifidelity surrogate modeling

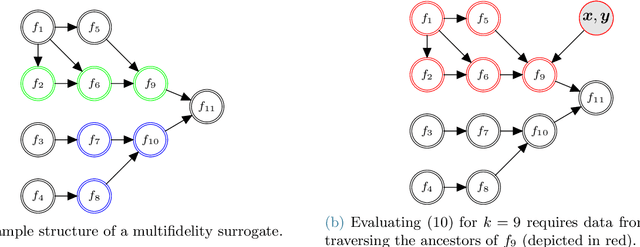
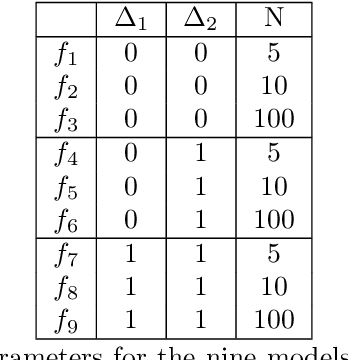
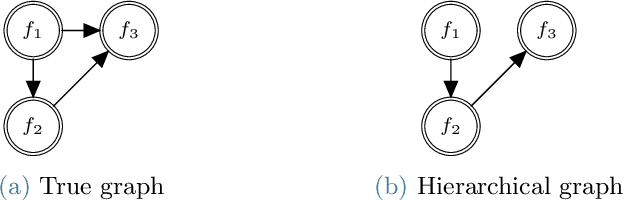
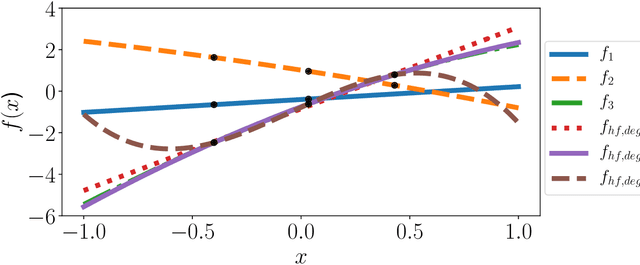
This paper presents an approach for constructing multifidelity surrogate models to simultaneously represent, and learn representations of, multiple information sources. The approach formulates a network of surrogate models whose relationships are defined via localized scalings and shifts. The network can have general structure, and can represent a significantly greater variety of modeling relationships than the hierarchical/recursive networks used in the current state of the art. We show empirically that this flexibility achieves greatest gains in the low-data regime, where the network structure must more efficiently leverage the connections between data sources to yield accurate predictions. We demonstrate our approach on four examples ranging from synthetic to physics-based simulation models. For the numerical test cases adopted here, we obtained an order-of-magnitude reduction in errors compared to multifidelity hierarchical and single-fidelity approaches.