NeurAM: nonlinear dimensionality reduction for uncertainty quantification through neural active manifolds

We present a new approach for nonlinear dimensionality reduction, specifically designed for computationally expensive mathematical models. We leverage autoencoders to discover a one-dimensional neural active manifold (NeurAM) capturing the model output variability, plus a simultaneously learnt surrogate model with inputs on this manifold. The proposed dimensionality reduction framework can then be applied to perform outer loop many-query tasks, like sensitivity analysis and uncertainty propagation. In particular, we prove, both theoretically under idealized conditions, and numerically in challenging test cases, how NeurAM can be used to obtain multifidelity sampling estimators with reduced variance by sampling the models on the discovered low-dimensional and shared manifold among models. Several numerical examples illustrate the main features of the proposed dimensionality reduction strategy, and highlight its advantages with respect to existing approaches in the literature.

A Probabilistic Neural Twin for Treatment Planning in Peripheral Pulmonary Artery Stenosis

The substantial computational cost of high-fidelity models in numerical hemodynamics has, so far, relegated their use mainly to offline treatment planning. New breakthroughs in data-driven architectures and optimization techniques for fast surrogate modeling provide an exciting opportunity to overcome these limitations, enabling the use of such technology for time-critical decisions. We discuss an application to the repair of multiple stenosis in peripheral pulmonary artery disease through either transcatheter pulmonary artery rehabilitation or surgery, where it is of interest to achieve desired pressures and flows at specific locations in the pulmonary artery tree, while minimizing the risk for the patient. Since different degrees of success can be achieved in practice during treatment, we formulate the problem in probability, and solve it through a sample-based approach. We propose a new offline-online pipeline for probabilsitic real-time treatment planning which combines offline assimilation of boundary conditions, model reduction, and training dataset generation with online estimation of marginal probabilities, possibly conditioned on the degree of augmentation observed in already repaired lesions. Moreover, we propose a new approach for the parametrization of arbitrarily shaped vascular repairs through iterative corrections of a zero-dimensional approximant. We demonstrate this pipeline for a diseased model of the pulmonary artery tree available through the Vascular Model Repository.

Minimax Classification with 0-1 Loss and Performance Guarantees

Supervised classification techniques use training samples to find classification rules with small expected 0-1 loss. Conventional methods achieve efficient learning and out-of-sample generalization by minimizing surrogate losses over specific families of rules. This paper presents minimax risk classifiers (MRCs) that do not rely on a choice of surrogate loss and family of rules. MRCs achieve efficient learning and out-of-sample generalization by minimizing worst-case expected 0-1 loss w.r.t. uncertainty sets that are defined by linear constraints and include the true underlying distribution. In addition, MRCs' learning stage provides performance guarantees as lower and upper tight bounds for expected 0-1 loss. We also present MRCs' finite-sample generalization bounds in terms of training size and smallest minimax risk, and show their competitive classification performance w.r.t. state-of-the-art techniques using benchmark datasets.

Supervised classification via minimax probabilistic transformations

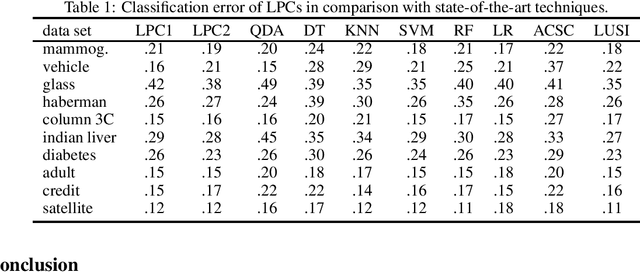
Current leaning techniques for supervised classification consider classification rules in specific families and empirically quantify performance using test data. Selection among families of classification rules, techniques' choices, parameters, etc. is mostly guided by an experimentation stage in which the performance of different options is estimated by computing the corresponding empirical risks over a set of test examples. This empirically-based system design is inefficient and not robust since it requires to test a possibly large pool of choices and it relies in the reliability of the empirical performance quantification. This paper presents classification algorithms that we call linear probabilistic machines (LPMs) that consider unconstrained classification rules and obtain tight performance guaranties during learning. LPMs utilize polyhedral uncertainty sets that contain the actual probability distribution with a tunable confidence and are defined by a functional that assigns features-label pairs to real numbers. LPMs achieve smaller worst-case risk against such uncertainty sets than any classification rule and their performance can be efficiently upper and lower bounded without testing.