Minimax Classification with 0-1 Loss and Performance Guarantees

Supervised classification techniques use training samples to find classification rules with small expected 0-1 loss. Conventional methods achieve efficient learning and out-of-sample generalization by minimizing surrogate losses over specific families of rules. This paper presents minimax risk classifiers (MRCs) that do not rely on a choice of surrogate loss and family of rules. MRCs achieve efficient learning and out-of-sample generalization by minimizing worst-case expected 0-1 loss w.r.t. uncertainty sets that are defined by linear constraints and include the true underlying distribution. In addition, MRCs' learning stage provides performance guarantees as lower and upper tight bounds for expected 0-1 loss. We also present MRCs' finite-sample generalization bounds in terms of training size and smallest minimax risk, and show their competitive classification performance w.r.t. state-of-the-art techniques using benchmark datasets.

Kernels of Mallows Models under the Hamming Distance for solving the Quadratic Assignment Problem

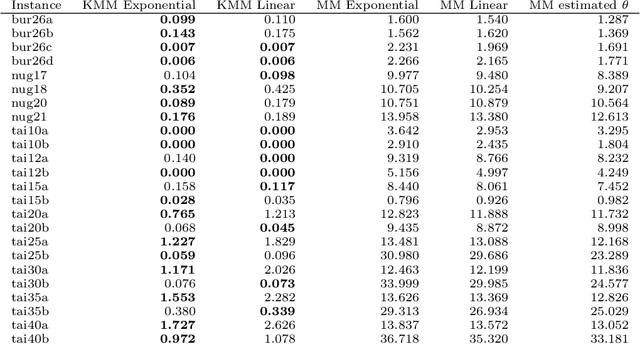
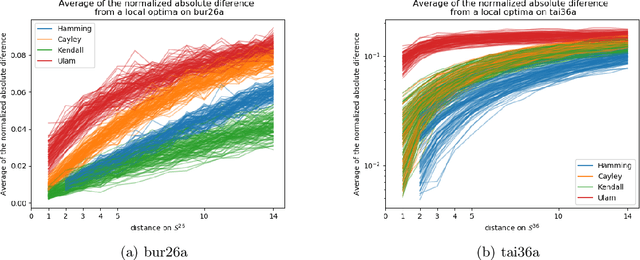
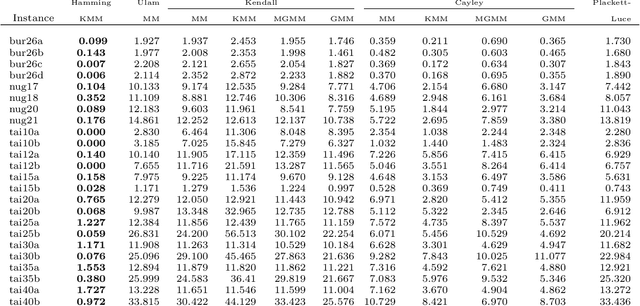
The Quadratic Assignment Problem (QAP) is a well-known permutation-based combinatorial optimization problem with real applications in industrial and logistics environments. Motivated by the challenge that this NP-hard problem represents, it has captured the attention of the evolutionary computation community for decades. As a result, a large number of algorithms have been proposed to optimize this algorithm. Among these, exact methods are only able to solve instances of size $n<40$, and thus, many heuristic and metaheuristic methods have been applied to the QAP. In this work, we follow this direction by approaching the QAP through Estimation of Distribution Algorithms (EDAs). Particularly, a non-parametric distance-based exponential probabilistic model is used. Based on the analysis of the characteristics of the QAP, and previous work in the area, we introduce Kernels of Mallows Model under the Hamming distance to the context of EDAs. Conducted experiments point out that the performance of the proposed algorithm in the QAP is superior to (i) the classical EDAs adapted to deal with the QAP, and also (ii) to the specific EDAs proposed in the literature to deal with permutation problems.

Online Ranking with Concept Drifts in Streaming Data

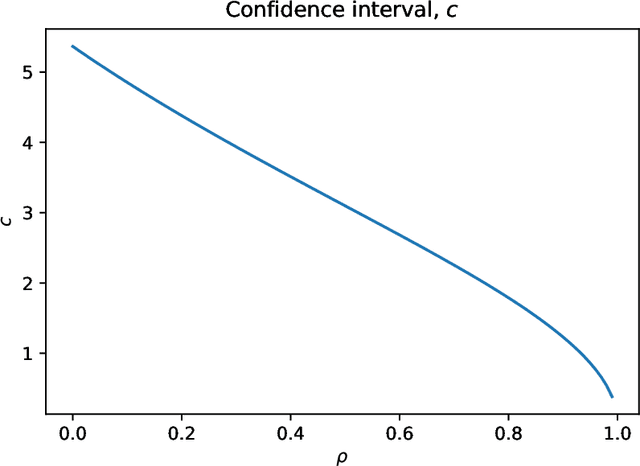
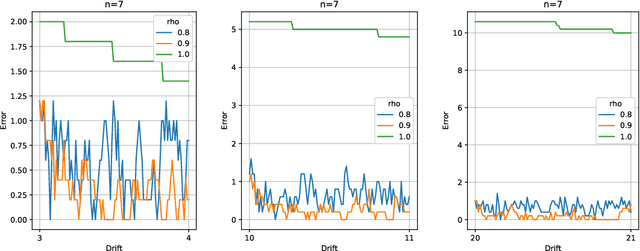
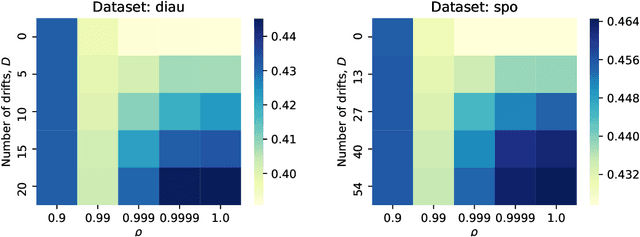
Two important problems in preference elicitation are rank aggregation and label ranking. Rank aggregation consists of finding a ranking that best summarizes a collection of preferences of some agents. The latter, label ranking, aims at learning a mapping between data instances and rankings defined over a finite set of categories or labels. This problem can effectively model many real application scenarios such as recommender systems. However, even when the preferences of populations usually change over time, related literature has so far addressed both problems over non-evolving preferences. This work deals with the problems of rank aggregation and label ranking over non-stationary data streams. In this context, there is a set of $n$ items and $m$ agents which provide their votes by casting a ranking of the $n$ items. The rankings are noisy realizations of an unknown probability distribution that changes over time. Our goal is to learn, in an online manner, the current ground truth distribution of rankings. We begin by proposing an aggregation function called Forgetful Borda (FBorda) that, using a forgetting mechanism, gives more importance to recently observed preferences. We prove that FBorda is a consistent estimator of the Kemeny ranking and lower bound the number of samples needed to learn the distribution while guaranteeing a certain level of confidence. Then, we develop a $k$-nearest neighbor classifier based on the proposed FBorda aggregation algorithm for the label ranking problem and demonstrate its accuracy in several scenarios of label ranking problem over evolving preferences.

Supervised classification via minimax probabilistic transformations

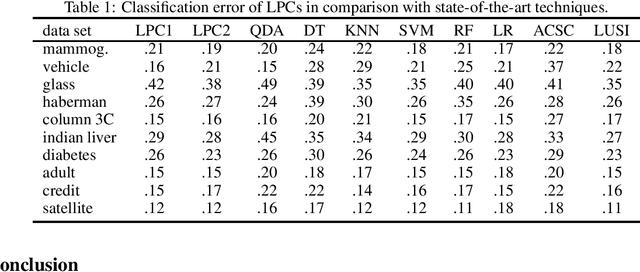
Current leaning techniques for supervised classification consider classification rules in specific families and empirically quantify performance using test data. Selection among families of classification rules, techniques' choices, parameters, etc. is mostly guided by an experimentation stage in which the performance of different options is estimated by computing the corresponding empirical risks over a set of test examples. This empirically-based system design is inefficient and not robust since it requires to test a possibly large pool of choices and it relies in the reliability of the empirical performance quantification. This paper presents classification algorithms that we call linear probabilistic machines (LPMs) that consider unconstrained classification rules and obtain tight performance guaranties during learning. LPMs utilize polyhedral uncertainty sets that contain the actual probability distribution with a tunable confidence and are defined by a functional that assigns features-label pairs to real numbers. LPMs achieve smaller worst-case risk against such uncertainty sets than any classification rule and their performance can be efficiently upper and lower bounded without testing.

General Supervision via Probabilistic Transformations

Different types of training data have led to numerous schemes for supervised classification. Current learning techniques are tailored to one specific scheme and cannot handle general ensembles of training data. This paper presents a unifying framework for supervised classification with general ensembles of training data, and proposes the learning methodology of generalized robust risk minimization (GRRM). The paper shows how current and novel supervision schemes can be addressed under the proposed framework by representing the relationship between examples at test and training via probabilistic transformations. The results show that GRRM can handle different types of training data in a unified manner, and enable new supervision schemes that aggregate general ensembles of training data.