Co-Optimization of Robot Design and Control: Enhancing Performance and Understanding Design Complexity

The design (shape) of a robot is usually decided before the control is implemented. This might limit how well the design is adapted to a task, as the suitability of the design is given by how well the robot performs in the task, which requires both a design and a controller. The co-optimization or simultaneous optimization of the design and control of robots addresses this limitation by producing a design and control that are both adapted to the task. In this paper, we investigate some of the challenges inherent in the co-optimization of design and control. We show that retraining the controller of a robot with additional resources after the co-optimization process terminates significantly improves the robot's performance. In addition, we demonstrate that the resources allocated to training the controller for each design influence the design complexity, where simpler designs are associated with lower training budgets. The experimentation is conducted in four publicly available simulation environments for co-optimization of design and control, making the findings more applicable to the general case. The results presented in this paper hope to guide other practitioners in the co-optimization of design and control of robots.

Speeding-up Evolutionary Algorithms to solve Black-Box Optimization Problems

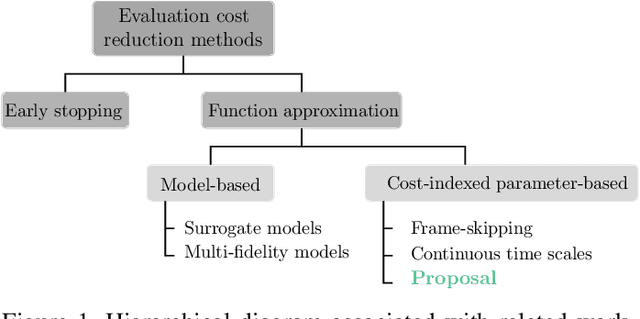
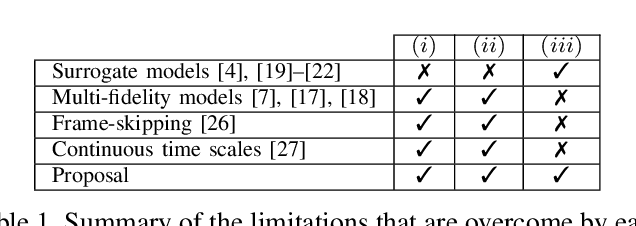
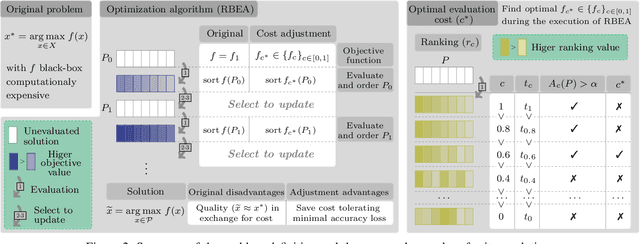
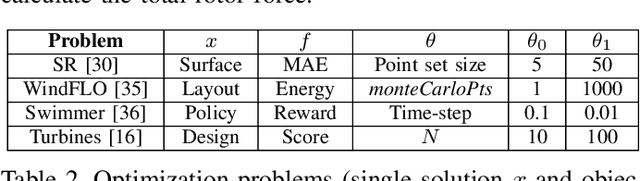
Population-based evolutionary algorithms are often considered when approaching computationally expensive black-box optimization problems. They employ a selection mechanism to choose the best solutions from a given population after comparing their objective values, which are then used to generate the next population. This iterative process explores the solution space efficiently, leading to improved solutions over time. However, these algorithms require a large number of evaluations to provide a quality solution, which might be computationally expensive when the evaluation cost is high. In some cases, it is possible to replace the original objective function with a less accurate approximation of lower cost. This introduces a trade-off between the evaluation cost and its accuracy. In this paper, we propose a technique capable of choosing an appropriate approximate function cost during the execution of the optimization algorithm. The proposal finds the minimum evaluation cost at which the solutions are still properly ranked, and consequently, more evaluations can be computed in the same amount of time with minimal accuracy loss. An experimental section on four very different problems reveals that the proposed approach can reach the same objective value in less than half of the time in certain cases.

Generalized Early Stopping in Evolutionary Direct Policy Search

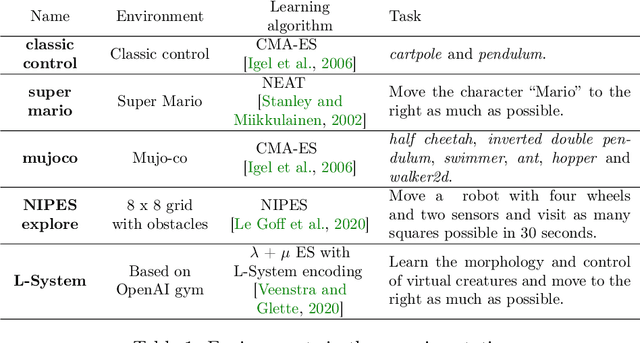
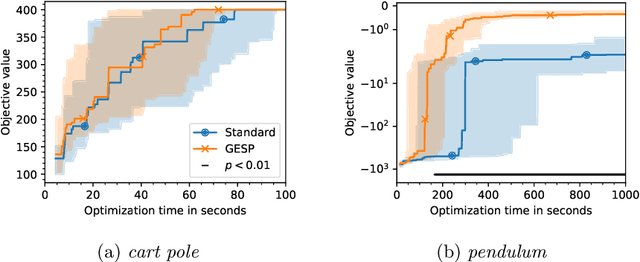
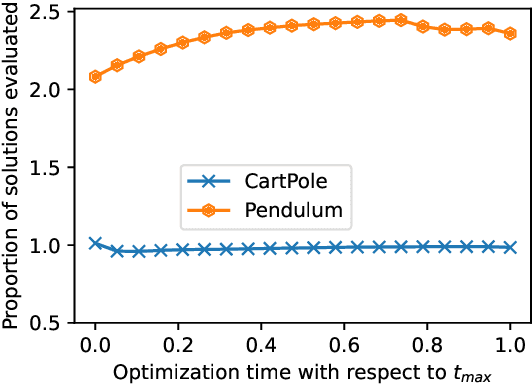
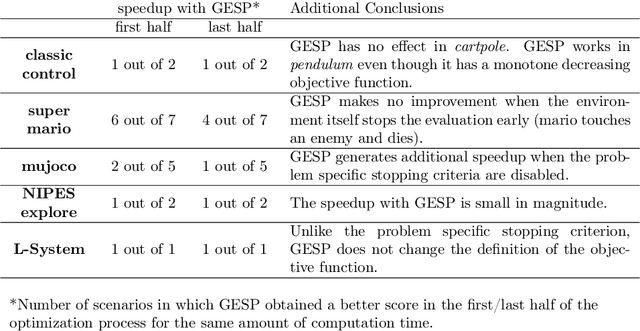
Lengthy evaluation times are common in many optimization problems such as direct policy search tasks, especially when they involve conducting evaluations in the physical world, e.g. in robotics applications. Often, when evaluating a solution over a fixed time period, it becomes clear that the objective value will not increase with additional computation time (for example, when a two-wheeled robot continuously spins on the spot). In such cases, it makes sense to stop the evaluation early to save computation time. However, most approaches to stop the evaluation are problem-specific and need to be specifically designed for the task at hand. Therefore, we propose an early stopping method for direct policy search. The proposed method only looks at the objective value at each time step and requires no problem-specific knowledge. We test the introduced stopping criterion in five direct policy search environments drawn from games, robotics, and classic control domains, and show that it can save up to 75% of the computation time. We also compare it with problem-specific stopping criteria and demonstrate that it performs comparably while being more generally applicable.

Comparing two samples through stochastic dominance: a graphical approach

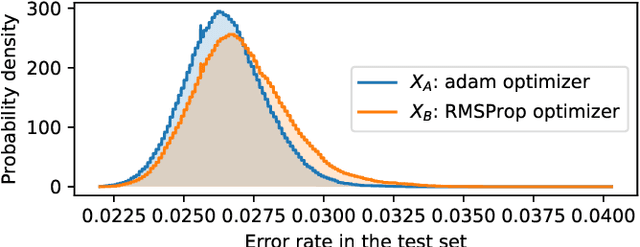
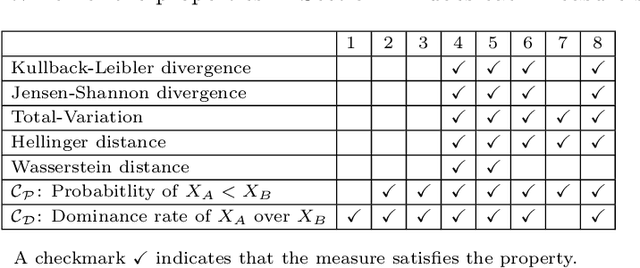
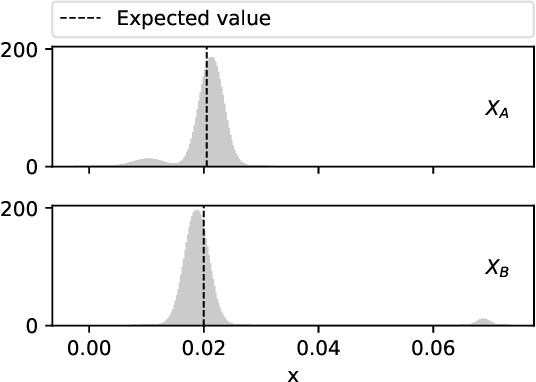
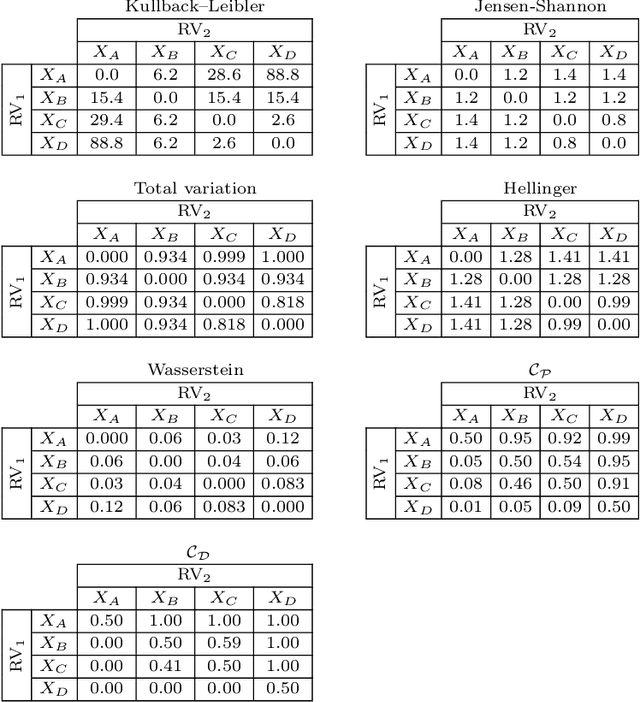
Non-deterministic measurements are common in real-world scenarios: the performance of a stochastic optimization algorithm or the total reward of a reinforcement learning agent in a chaotic environment are just two examples in which unpredictable outcomes are common. These measures can be modeled as random variables and compared among each other via their expected values or more sophisticated tools such as null hypothesis statistical tests. In this paper, we propose an alternative framework to visually compare two samples according to their estimated cumulative distribution functions. First, we introduce a dominance measure for two random variables that quantifies the proportion in which the cumulative distribution function of one of the random variables scholastically dominates the other one. Then, we present a graphical method that decomposes in quantiles i) the proposed dominance measure and ii) the probability that one of the random variables takes lower values than the other. With illustrative purposes, we re-evaluate the experimentation of an already published work with the proposed methodology and we show that additional conclusions (missed by the rest of the methods) can be inferred. Additionally, the software package RVCompare was created as a convenient way of applying and experimenting with the proposed framework.

Kernels of Mallows Models under the Hamming Distance for solving the Quadratic Assignment Problem

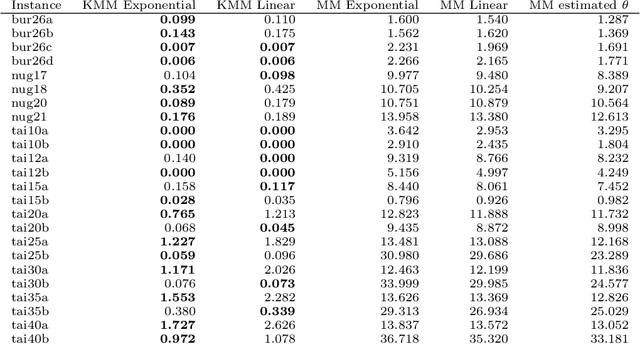
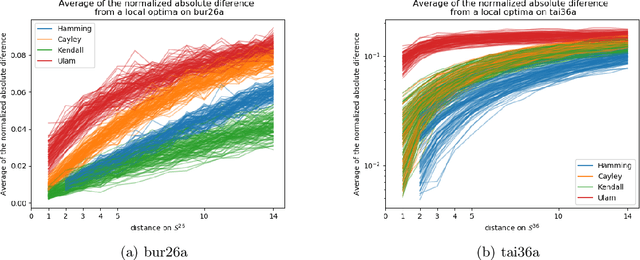
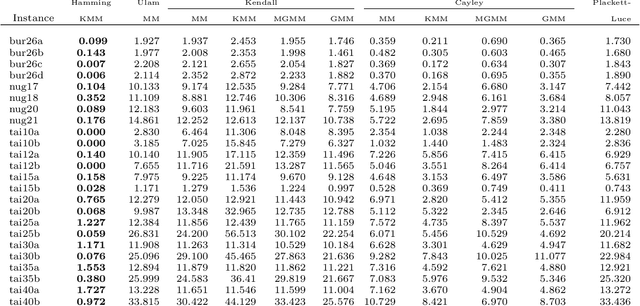
The Quadratic Assignment Problem (QAP) is a well-known permutation-based combinatorial optimization problem with real applications in industrial and logistics environments. Motivated by the challenge that this NP-hard problem represents, it has captured the attention of the evolutionary computation community for decades. As a result, a large number of algorithms have been proposed to optimize this algorithm. Among these, exact methods are only able to solve instances of size $n<40$, and thus, many heuristic and metaheuristic methods have been applied to the QAP. In this work, we follow this direction by approaching the QAP through Estimation of Distribution Algorithms (EDAs). Particularly, a non-parametric distance-based exponential probabilistic model is used. Based on the analysis of the characteristics of the QAP, and previous work in the area, we introduce Kernels of Mallows Model under the Hamming distance to the context of EDAs. Conducted experiments point out that the performance of the proposed algorithm in the QAP is superior to (i) the classical EDAs adapted to deal with the QAP, and also (ii) to the specific EDAs proposed in the literature to deal with permutation problems.