Decentralized Federated Learning of Probabilistic Generative Classifiers

Federated learning is a paradigm of increasing relevance in real world applications, aimed at building a global model across a network of heterogeneous users without requiring the sharing of private data. We focus on model learning over decentralized architectures, where users collaborate directly to update the global model without relying on a central server. In this context, the current paper proposes a novel approach to collaboratively learn probabilistic generative classifiers with a parametric form. The framework is composed by a communication network over a set of local nodes, each of one having its own local data, and a local updating rule. The proposal involves sharing local statistics with neighboring nodes, where each node aggregates the neighbors' information and iteratively learns its own local classifier, which progressively converges to a global model. Extensive experiments demonstrate that the algorithm consistently converges to a globally competitive model across a wide range of network topologies, network sizes, local dataset sizes, and extreme non-i.i.d. data distributions.

Risk-based Calibration for Probabilistic Classifiers

We introduce a general iterative procedure called risk-based calibration (RC) designed to minimize the empirical risk under the 0-1 loss (empirical error) for probabilistic classifiers. These classifiers are based on modeling probability distributions, including those constructed from the joint distribution (generative) and those based on the class conditional distribution (conditional). RC can be particularized to any probabilistic classifier provided a specific learning algorithm that computes the classifier's parameters in closed form using data statistics. RC reinforces the statistics aligned with the true class while penalizing those associated with other classes, guided by the 0-1 loss. The proposed method has been empirically tested on 30 datasets using na\"ive Bayes, quadratic discriminant analysis, and logistic regression classifiers. RC improves the empirical error of the original closed-form learning algorithms and, more notably, consistently outperforms the gradient descent approach with the three classifiers.

PAC-Bayes-Chernoff bounds for unbounded losses

We present a new high-probability PAC-Bayes oracle bound for unbounded losses. This result can be understood as a PAC-Bayes version of the Chernoff bound. The proof technique relies on uniformly bounding the tail of certain random variable based on the Cram\'er transform of the loss. We highlight two applications of our main result. First, we show that our bound solves the open problem of optimizing the free parameter on many PAC-Bayes bounds. Finally, we show that our approach allows working with flexible assumptions on the loss function, resulting in novel bounds that generalize previous ones and can be minimized to obtain Gibbs-like posteriors.

Time-dependent Probabilistic Generative Models for Disease Progression

Electronic health records contain valuable information for monitoring patients' health trajectories over time. Disease progression models have been developed to understand the underlying patterns and dynamics of diseases using these data as sequences. However, analyzing temporal data from EHRs is challenging due to the variability and irregularities present in medical records. We propose a Markovian generative model of treatments developed to (i) model the irregular time intervals between medical events; (ii) classify treatments into subtypes based on the patient sequence of medical events and the time intervals between them; and (iii) segment treatments into subsequences of disease progression patterns. We assume that sequences have an associated structure of latent variables: a latent class representing the different subtypes of treatments; and a set of latent stages indicating the phase of progression of the treatments. We use the Expectation-Maximization algorithm to learn the model, which is efficiently solved with a dynamic programming-based method. Various parametric models have been employed to model the time intervals between medical events during the learning process, including the geometric, exponential, and Weibull distributions. The results demonstrate the effectiveness of our model in recovering the underlying model from data and accurately modeling the irregular time intervals between medical actions.

Speeding-up Evolutionary Algorithms to solve Black-Box Optimization Problems

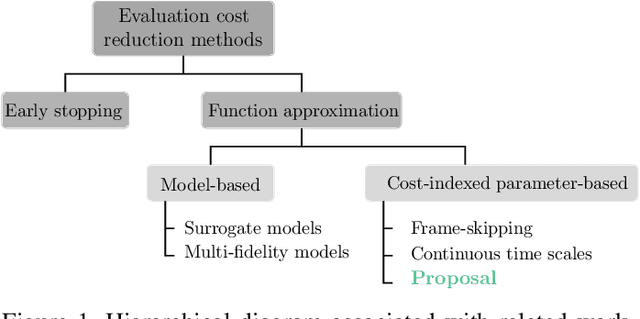
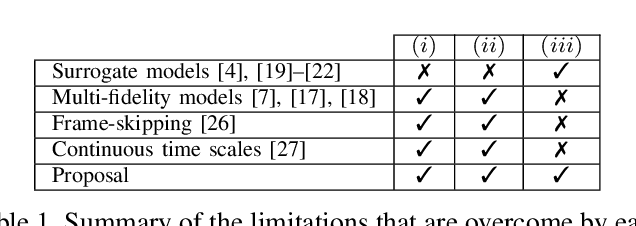
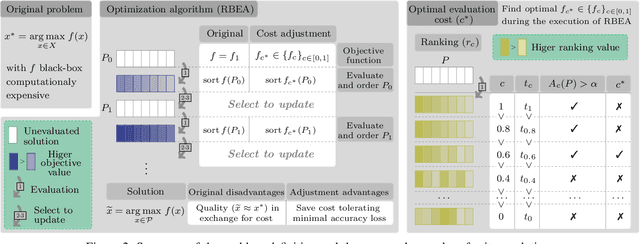
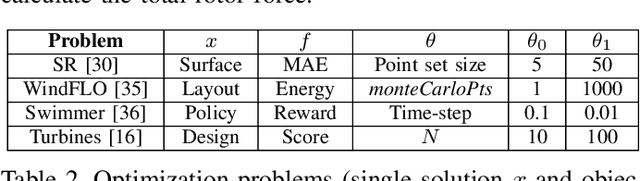
Population-based evolutionary algorithms are often considered when approaching computationally expensive black-box optimization problems. They employ a selection mechanism to choose the best solutions from a given population after comparing their objective values, which are then used to generate the next population. This iterative process explores the solution space efficiently, leading to improved solutions over time. However, these algorithms require a large number of evaluations to provide a quality solution, which might be computationally expensive when the evaluation cost is high. In some cases, it is possible to replace the original objective function with a less accurate approximation of lower cost. This introduces a trade-off between the evaluation cost and its accuracy. In this paper, we propose a technique capable of choosing an appropriate approximate function cost during the execution of the optimization algorithm. The proposal finds the minimum evaluation cost at which the solutions are still properly ranked, and consequently, more evaluations can be computed in the same amount of time with minimal accuracy loss. An experimental section on four very different problems reveals that the proposed approach can reach the same objective value in less than half of the time in certain cases.

Efficient Learning of Minimax Risk Classifiers in High Dimensions

High-dimensional data is common in multiple areas, such as health care and genomics, where the number of features can be tens of thousands. In such scenarios, the large number of features often leads to inefficient learning. Constraint generation methods have recently enabled efficient learning of L1-regularized support vector machines (SVMs). In this paper, we leverage such methods to obtain an efficient learning algorithm for the recently proposed minimax risk classifiers (MRCs). The proposed iterative algorithm also provides a sequence of worst-case error probabilities and performs feature selection. Experiments on multiple high-dimensional datasets show that the proposed algorithm is efficient in high-dimensional scenarios. In addition, the worst-case error probability provides useful information about the classifier performance, and the features selected by the algorithm are competitive with the state-of-the-art.

Dirichlet process mixture models for non-stationary data streams

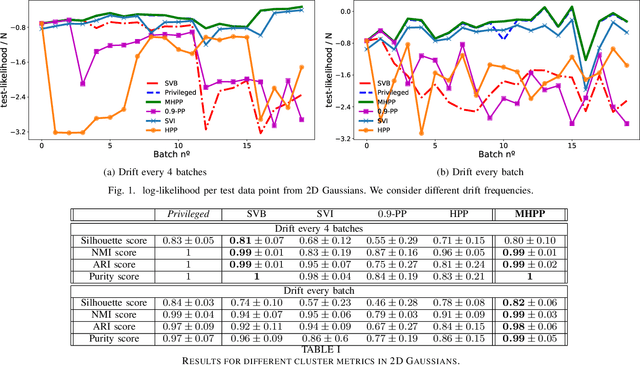
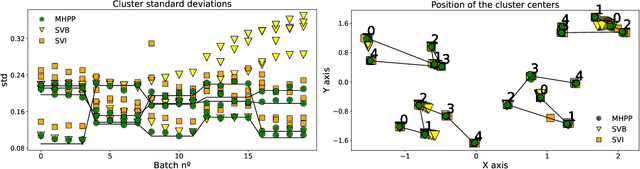
In recent years, we have seen a handful of work on inference algorithms over non-stationary data streams. Given their flexibility, Bayesian non-parametric models are a good candidate for these scenarios. However, reliable streaming inference under the concept drift phenomenon is still an open problem for these models. In this work, we propose a variational inference algorithm for Dirichlet process mixture models. Our proposal deals with the concept drift by including an exponential forgetting over the prior global parameters. Our algorithm allows to adapt the learned model to the concept drifts automatically. We perform experiments in both synthetic and real data, showing that the proposed model is competitive with the state-of-the-art algorithms in the density estimation problem, and it outperforms them in the clustering problem.

Semantic Clustering of a Sequence of Satellite Images

Satellite images constitute a highly valuable and abundant resource for many real world applications. However, the labeled data needed to train most machine learning models are scarce and difficult to obtain. In this context, the current work investigates a fully unsupervised methodology that, given a temporal sequence of satellite images, creates a partition of the ground according to its semantic properties and their evolution over time. The sequences of images are translated into a grid of multivariate time series of embedded tiles. The embedding and the partitional clustering of these sequences of tiles are constructed in two iterative steps: In the first step, the embedding is able to extract the information of the sequences of tiles based on a geographical neighborhood, and the tiles are grouped into clusters. In the second step, the embedding is refined by using the neighborhood defined by the clusters, and the final clustering of the sequences of tiles is obtained. We illustrate the methodology by conducting the semantic clustering of a sequence of 20 satellite images of the region of Navarra (Spain). The results show that the clustering of multivariate time series is robust and contains trustful spatio-temporal semantic information about the region under study. We unveil the close connection that exists between the geographic and embedded spaces, and find out that the semantic properties attributed to these kinds of embeddings are fully exploited and even enhanced by the proposed clustering of time series.

Comparing two samples through stochastic dominance: a graphical approach

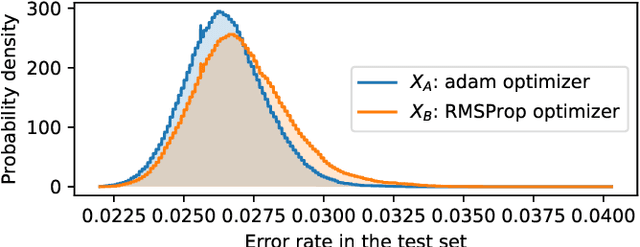
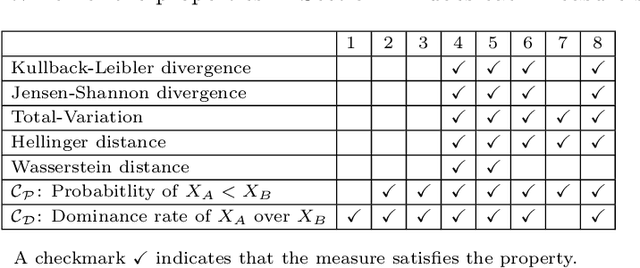
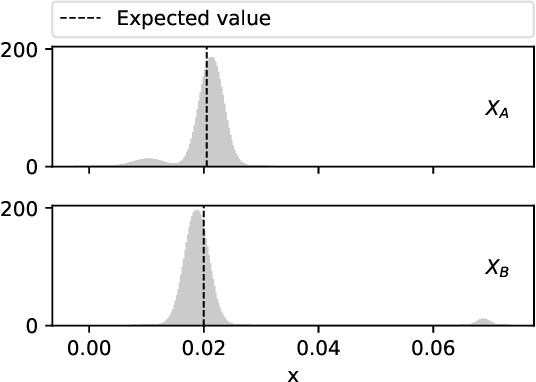
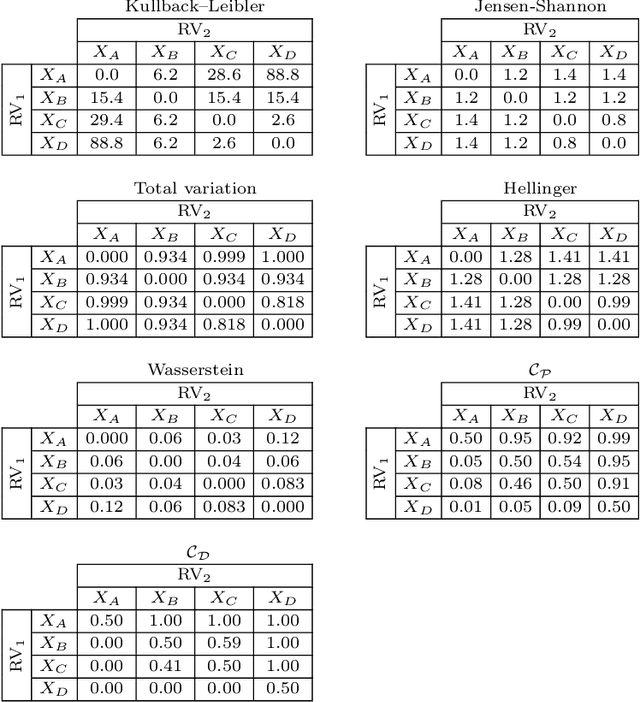
Non-deterministic measurements are common in real-world scenarios: the performance of a stochastic optimization algorithm or the total reward of a reinforcement learning agent in a chaotic environment are just two examples in which unpredictable outcomes are common. These measures can be modeled as random variables and compared among each other via their expected values or more sophisticated tools such as null hypothesis statistical tests. In this paper, we propose an alternative framework to visually compare two samples according to their estimated cumulative distribution functions. First, we introduce a dominance measure for two random variables that quantifies the proportion in which the cumulative distribution function of one of the random variables scholastically dominates the other one. Then, we present a graphical method that decomposes in quantiles i) the proposed dominance measure and ii) the probability that one of the random variables takes lower values than the other. With illustrative purposes, we re-evaluate the experimentation of an already published work with the proposed methodology and we show that additional conclusions (missed by the rest of the methods) can be inferred. Additionally, the software package RVCompare was created as a convenient way of applying and experimenting with the proposed framework.

MRCpy: A Library for Minimax Risk Classifiers

Existing libraries for supervised classification implement techniques that are based on empirical risk minimization and utilize surrogate losses. We present MRCpy library that implements minimax risk classifiers (MRCs) that are based on robust risk minimization and can utilize 0-1-loss. Such techniques give rise to a manifold of classification methods that can provide tight bounds on the expected loss. MRCpy provides a unified interface for different variants of MRCs and follows the standards of popular Python libraries. The presented library also provides implementation for popular techniques that can be seen as MRCs such as L1-regularized logistic regression, zero-one adversarial, and maximum entropy machines. In addition, MRCpy implements recent feature mappings such as Fourier, ReLU, and threshold features. The library is designed with an object-oriented approach that facilitates collaborators and users.