Passive Approach for the K-means Problem on Streaming Data
Paper and Code
Dec 07, 2020
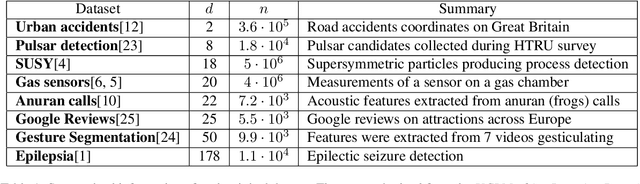

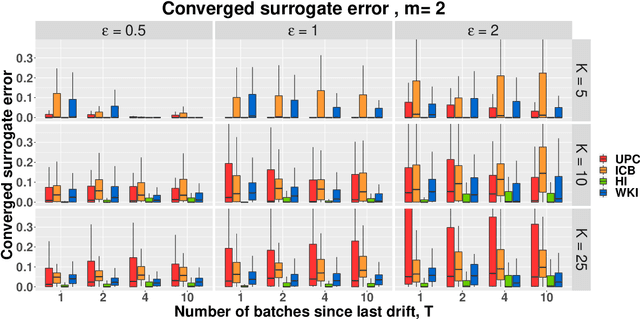
Currently the amount of data produced worldwide is increasing beyond measure, thus a high volume of unsupervised data must be processed continuously. One of the main unsupervised data analysis is clustering. In streaming data scenarios, the data is composed by an increasing sequence of batches of samples where the concept drift phenomenon may happen. In this paper, we formally define the Streaming $K$-means(S$K$M) problem, which implies a restart of the error function when a concept drift occurs. We propose a surrogate error function that does not rely on concept drift detection. We proof that the surrogate is a good approximation of the S$K$M error. Hence, we suggest an algorithm which minimizes this alternative error each time a new batch arrives. We present some initialization techniques for streaming data scenarios as well. Besides providing theoretical results, experiments demonstrate an improvement of the converged error for the non-trivial initialization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge