PAC-Bayes-Chernoff bounds for unbounded losses

We present a new high-probability PAC-Bayes oracle bound for unbounded losses. This result can be understood as a PAC-Bayes version of the Chernoff bound. The proof technique relies on uniformly bounding the tail of certain random variable based on the Cram\'er transform of the loss. We highlight two applications of our main result. First, we show that our bound solves the open problem of optimizing the free parameter on many PAC-Bayes bounds. Finally, we show that our approach allows working with flexible assumptions on the loss function, resulting in novel bounds that generalize previous ones and can be minimized to obtain Gibbs-like posteriors.

Dirichlet process mixture models for non-stationary data streams

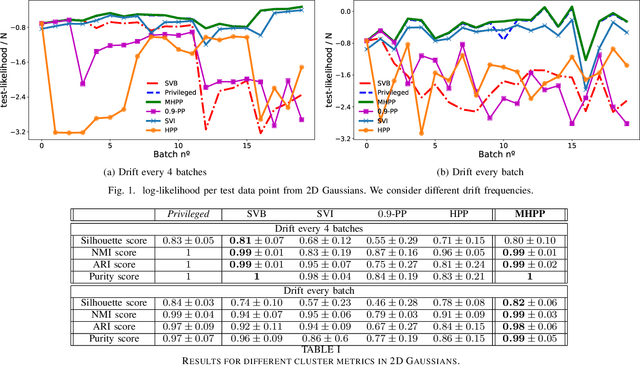
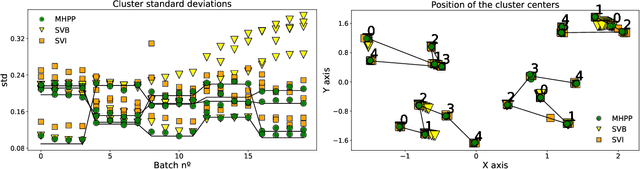
In recent years, we have seen a handful of work on inference algorithms over non-stationary data streams. Given their flexibility, Bayesian non-parametric models are a good candidate for these scenarios. However, reliable streaming inference under the concept drift phenomenon is still an open problem for these models. In this work, we propose a variational inference algorithm for Dirichlet process mixture models. Our proposal deals with the concept drift by including an exponential forgetting over the prior global parameters. Our algorithm allows to adapt the learned model to the concept drifts automatically. We perform experiments in both synthetic and real data, showing that the proposed model is competitive with the state-of-the-art algorithms in the density estimation problem, and it outperforms them in the clustering problem.