Fixed-Mean Gaussian Processes for Post-hoc Bayesian Deep Learning

Recently, there has been an increasing interest in performing post-hoc uncertainty estimation about the predictions of pre-trained deep neural networks (DNNs). Given a pre-trained DNN via back-propagation, these methods enhance the original network by adding output confidence measures, such as error bars, without compromising its initial accuracy. In this context, we introduce a novel family of sparse variational Gaussian processes (GPs), where the posterior mean is fixed to any continuous function when using a universal kernel. Specifically, we fix the mean of this GP to the output of the pre-trained DNN, allowing our approach to effectively fit the GP's predictive variances to estimate the DNN prediction uncertainty. Our approach leverages variational inference (VI) for efficient stochastic optimization, with training costs that remain independent of the number of training points, scaling efficiently to large datasets such as ImageNet. The proposed method, called fixed mean GP (FMGP), is architecture-agnostic, relying solely on the pre-trained model's outputs to adjust the predictive variances. Experimental results demonstrate that FMGP improves both uncertainty estimation and computational efficiency when compared to state-of-the-art methods.

PAC-Bayes-Chernoff bounds for unbounded losses

We present a new high-probability PAC-Bayes oracle bound for unbounded losses. This result can be understood as a PAC-Bayes version of the Chernoff bound. The proof technique relies on uniformly bounding the tail of certain random variable based on the Cram\'er transform of the loss. We highlight two applications of our main result. First, we show that our bound solves the open problem of optimizing the free parameter on many PAC-Bayes bounds. Finally, we show that our approach allows working with flexible assumptions on the loss function, resulting in novel bounds that generalize previous ones and can be minimized to obtain Gibbs-like posteriors.

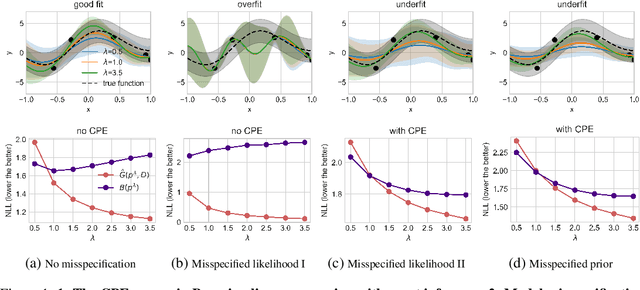
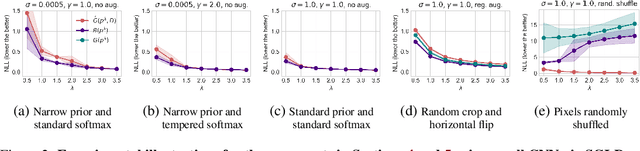
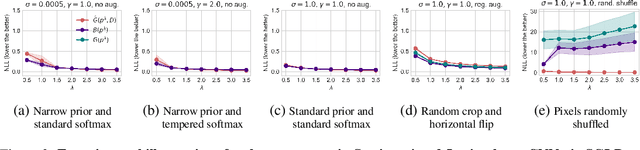
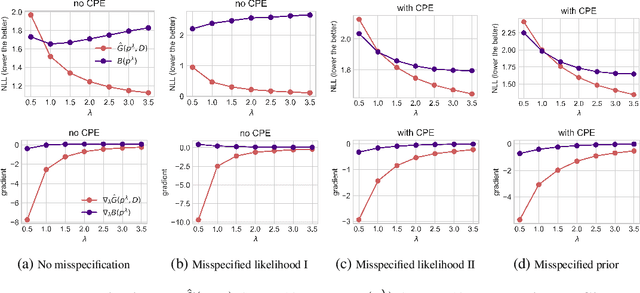
If there is no underfitting, there is no Cold Posterior Effect

The cold posterior effect (CPE) (Wenzel et al., 2020) in Bayesian deep learning shows that, for posteriors with a temperature $T<1$, the resulting posterior predictive could have better performances than the Bayesian posterior ($T=1$). As the Bayesian posterior is known to be optimal under perfect model specification, many recent works have studied the presence of CPE as a model misspecification problem, arising from the prior and/or from the likelihood function. In this work, we provide a more nuanced understanding of the CPE as we show that misspecification leads to CPE only when the resulting Bayesian posterior underfits. In fact, we theoretically show that if there is no underfitting, there is no CPE.

Understanding Generalization in the Interpolation Regime using the Rate Function

In this paper, we present a novel characterization of the smoothness of a model based on basic principles of Large Deviation Theory. In contrast to prior work, where the smoothness of a model is normally characterized by a real value (e.g., the weights' norm), we show that smoothness can be described by a simple real-valued function. Based on this concept of smoothness, we propose an unifying theoretical explanation of why some interpolators generalize remarkably well and why a wide range of modern learning techniques (i.e., stochastic gradient descent, $\ell_2$-norm regularization, data augmentation, invariant architectures, and overparameterization) are able to find them. The emergent conclusion is that all these methods provide complimentary procedures that bias the optimizer to smoother interpolators, which, according to this theoretical analysis, are the ones with better generalization error.

Variational Linearized Laplace Approximation for Bayesian Deep Learning

Pre-trained deep neural networks can be adapted to perform uncertainty estimation by transforming them into Bayesian neural networks via methods such as Laplace approximation (LA) or its linearized form (LLA), among others. To make these methods more tractable, the generalized Gauss-Newton (GGN) approximation is often used. However, due to complex inefficiency difficulties, both LA and LLA rely on further approximations, such as Kronecker-factored or diagonal approximate GGN matrices, which can affect the results. To address these issues, we propose a new method for scaling LLA using a variational sparse Gaussian Process (GP) approximation based on the dual RKHS of GPs. Our method retains the predictive mean of the original model while allowing for efficient stochastic optimization and scalability in both the number of parameters and the size of the training dataset. Moreover, its training cost is independent of the number of training points, improving over previously existing methods. Our preliminary experiments indicate that it outperforms already existing efficient variants of LLA, such as accelerated LLA (ELLA), based on the Nystr\"om approximation.

Correcting Model Bias with Sparse Implicit Processes

Model selection in machine learning (ML) is a crucial part of the Bayesian learning procedure. Model choice may impose strong biases on the resulting predictions, which can hinder the performance of methods such as Bayesian neural networks and neural samplers. On the other hand, newly proposed approaches for Bayesian ML exploit features of approximate inference in function space with implicit stochastic processes (a generalization of Gaussian processes). The approach of Sparse Implicit Processes (SIP) is particularly successful in this regard, since it is fully trainable and achieves flexible predictions. Here, we expand on the original experiments to show that SIP is capable of correcting model bias when the data generating mechanism differs strongly from the one implied by the model. We use synthetic datasets to show that SIP is capable of providing predictive distributions that reflect the data better than the exact predictions of the initial, but wrongly assumed model.

Deep Variational Implicit Processes

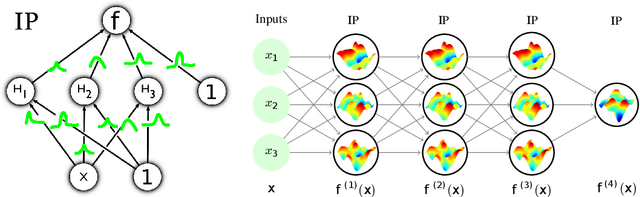
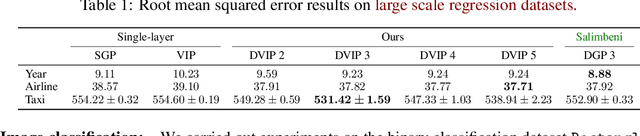
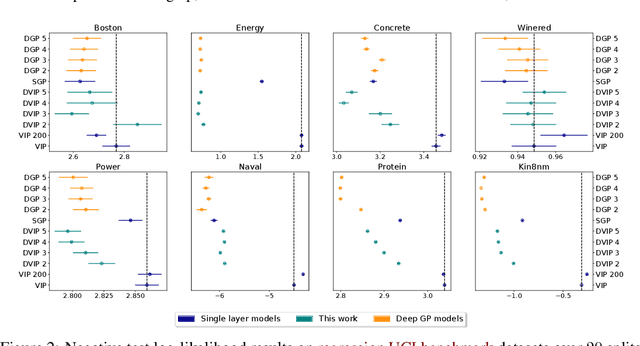
Implicit processes (IPs) are a generalization of Gaussian processes (GPs). IPs may lack a closed-form expression but are easy to sample from. Examples include, among others, Bayesian neural networks or neural samplers. IPs can be used as priors over functions, resulting in flexible models with well-calibrated prediction uncertainty estimates. Methods based on IPs usually carry out function-space approximate inference, which overcomes some of the difficulties of parameter-space approximate inference. Nevertheless, the approximations employed often limit the expressiveness of the final model, resulting, \emph{e.g.}, in a Gaussian predictive distribution, which can be restrictive. We propose here a multi-layer generalization of IPs called the Deep Variational Implicit process (DVIP). This generalization is similar to that of deep GPs over GPs, but it is more flexible due to the use of IPs as the prior distribution over the latent functions. We describe a scalable variational inference algorithm for training DVIP and show that it outperforms previous IP-based methods and also deep GPs. We support these claims via extensive regression and classification experiments. We also evaluate DVIP on large datasets with up to several million data instances to illustrate its good scalability and performance.

Diversity and Generalization in Neural Network Ensembles

Ensembles are widely used in machine learning and, usually, provide state-of-the-art performance in many prediction tasks. From the very beginning, the diversity of an ensemble has been identified as a key factor for the superior performance of these models. But the exact role that diversity plays in ensemble models is poorly understood, specially in the context of neural networks. In this work, we combine and expand previously published results in a theoretically sound framework that describes the relationship between diversity and ensemble performance for a wide range of ensemble methods. More precisely, we provide sound answers to the following questions: how to measure diversity, how diversity relates to the generalization error of an ensemble, and how diversity is promoted by neural network ensemble algorithms. This analysis covers three widely used loss functions, namely, the squared loss, the cross-entropy loss, and the 0-1 loss; and two widely used model combination strategies, namely, model averaging and weighted majority vote. We empirically validate this theoretical analysis with neural network ensembles.