Variational Linearized Laplace Approximation for Bayesian Deep Learning

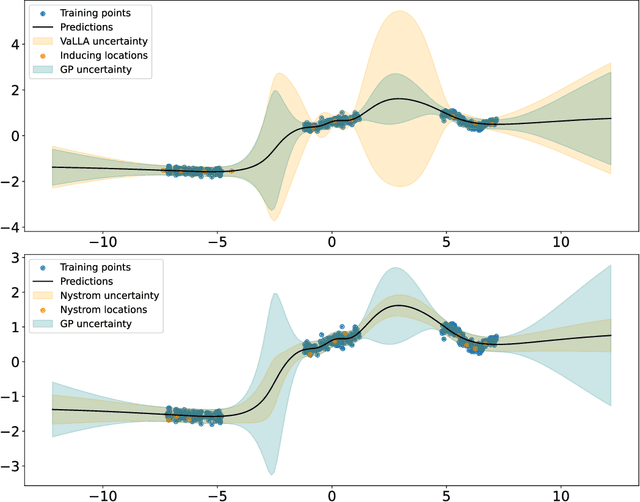
Pre-trained deep neural networks can be adapted to perform uncertainty estimation by transforming them into Bayesian neural networks via methods such as Laplace approximation (LA) or its linearized form (LLA), among others. To make these methods more tractable, the generalized Gauss-Newton (GGN) approximation is often used. However, due to complex inefficiency difficulties, both LA and LLA rely on further approximations, such as Kronecker-factored or diagonal approximate GGN matrices, which can affect the results. To address these issues, we propose a new method for scaling LLA using a variational sparse Gaussian Process (GP) approximation based on the dual RKHS of GPs. Our method retains the predictive mean of the original model while allowing for efficient stochastic optimization and scalability in both the number of parameters and the size of the training dataset. Moreover, its training cost is independent of the number of training points, improving over previously existing methods. Our preliminary experiments indicate that it outperforms already existing efficient variants of LLA, such as accelerated LLA (ELLA), based on the Nystr\"om approximation.

Correcting Model Bias with Sparse Implicit Processes

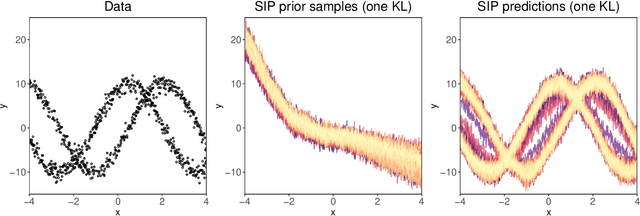
Model selection in machine learning (ML) is a crucial part of the Bayesian learning procedure. Model choice may impose strong biases on the resulting predictions, which can hinder the performance of methods such as Bayesian neural networks and neural samplers. On the other hand, newly proposed approaches for Bayesian ML exploit features of approximate inference in function space with implicit stochastic processes (a generalization of Gaussian processes). The approach of Sparse Implicit Processes (SIP) is particularly successful in this regard, since it is fully trainable and achieves flexible predictions. Here, we expand on the original experiments to show that SIP is capable of correcting model bias when the data generating mechanism differs strongly from the one implied by the model. We use synthetic datasets to show that SIP is capable of providing predictive distributions that reflect the data better than the exact predictions of the initial, but wrongly assumed model.

Deep Variational Implicit Processes

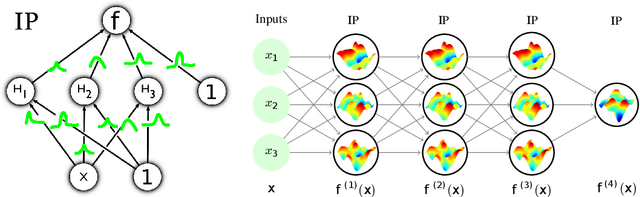
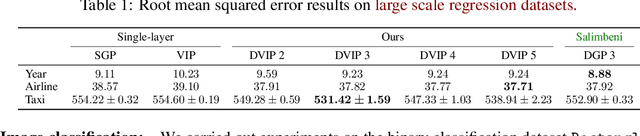
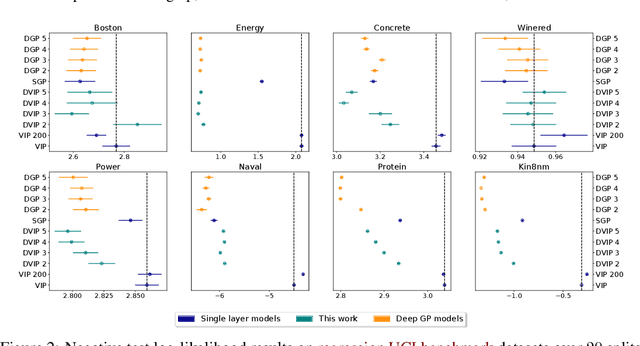
Implicit processes (IPs) are a generalization of Gaussian processes (GPs). IPs may lack a closed-form expression but are easy to sample from. Examples include, among others, Bayesian neural networks or neural samplers. IPs can be used as priors over functions, resulting in flexible models with well-calibrated prediction uncertainty estimates. Methods based on IPs usually carry out function-space approximate inference, which overcomes some of the difficulties of parameter-space approximate inference. Nevertheless, the approximations employed often limit the expressiveness of the final model, resulting, \emph{e.g.}, in a Gaussian predictive distribution, which can be restrictive. We propose here a multi-layer generalization of IPs called the Deep Variational Implicit process (DVIP). This generalization is similar to that of deep GPs over GPs, but it is more flexible due to the use of IPs as the prior distribution over the latent functions. We describe a scalable variational inference algorithm for training DVIP and show that it outperforms previous IP-based methods and also deep GPs. We support these claims via extensive regression and classification experiments. We also evaluate DVIP on large datasets with up to several million data instances to illustrate its good scalability and performance.

Sparse Implicit Processes for Approximate Inference

Implicit Processes (IPs) are flexible priors that can describe models such as Bayesian neural networks, neural samplers and data generators. IPs allow for approximate inference in function-space. This avoids some degenerate problems of parameter-space approximate inference due to the high number of parameters and strong dependencies. For this, an extra IP is often used to approximate the posterior of the prior IP. However, simultaneously adjusting the parameters of the prior IP and the approximate posterior IP is a challenging task. Existing methods that can tune the prior IP result in a Gaussian predictive distribution, which fails to capture important data patterns. By contrast, methods producing flexible predictive distributions by using another IP to approximate the posterior process cannot fit the prior IP to the observed data. We propose here a method that can carry out both tasks. For this, we rely on an inducing-point representation of the prior IP, as often done in the context of sparse Gaussian processes. The result is a scalable method for approximate inference with IPs that can tune the prior IP parameters to the data, and that provides accurate non-Gaussian predictive distributions.

Adversarial $α$-divergence Minimization for Bayesian Approximate Inference

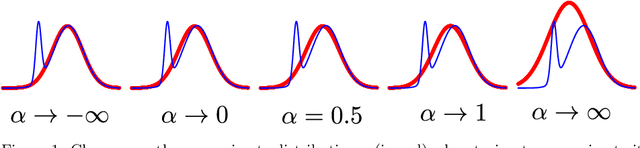
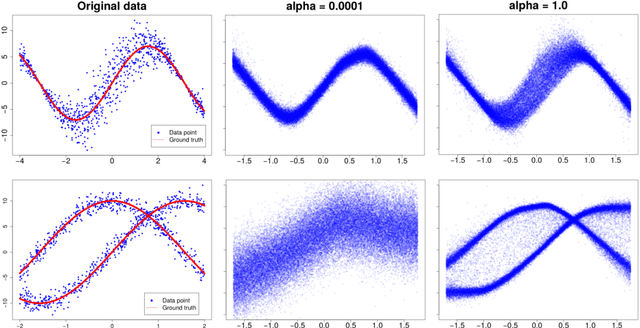
Neural networks are popular models for regression. They are often trained via back-propagation to find a value of the weights that correctly predicts the observed data. Although back-propagation has shown good performance in many applications, it cannot easily output an estimate of the uncertainty in the predictions made. Measuring this uncertainty in the predictions of machine learning models is a critical aspect with important applications. Uncertainty estimates can be obtained by following a Bayesian approach in which a posterior distribution of the model parameters is computed. The posterior distribution summarizes which parameter values are compatible with the data. Typically,this posterior distribution is intractable and has to be approximated. Several approaches have been considered for solving this problem. We propose here a general method for approximate Bayesian inference based on minimizing{\alpha}-divergences which allows for flexible approximate distributions. The method is evaluated in the context of Bayesian neural networks for regression on extensive experiments. The results show that it often gives better performance in terms of the test log-likelihood and sometimes in terms of the squared error.