Stochastic automatic differentiation for Monte Carlo processes

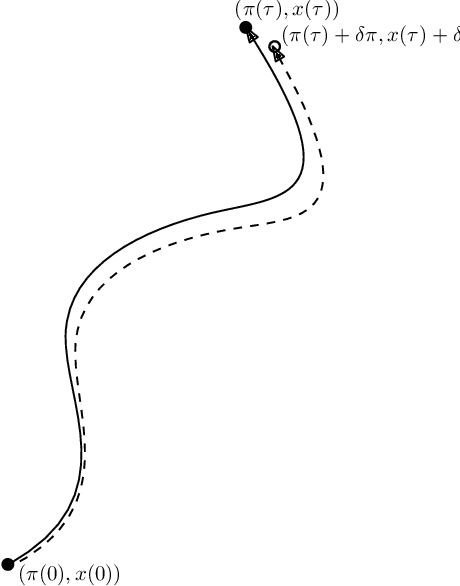
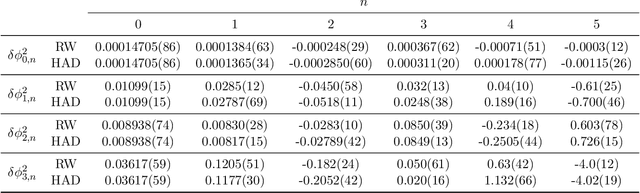
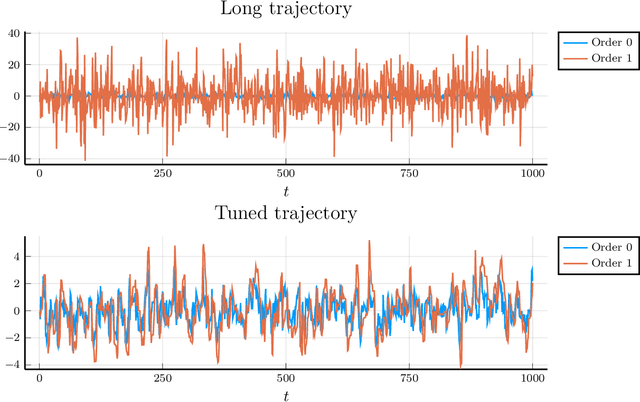
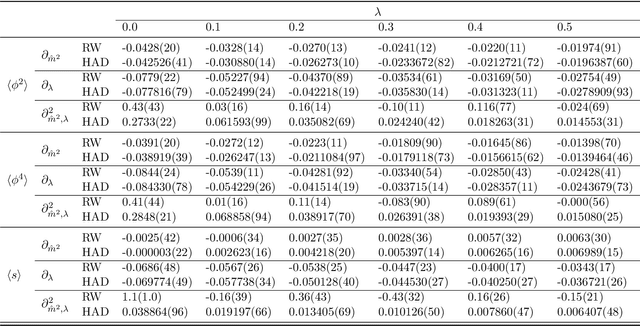
Monte Carlo methods represent a cornerstone of computer science. They allow to sample high dimensional distribution functions in an efficient way. In this paper we consider the extension of Automatic Differentiation (AD) techniques to Monte Carlo process, addressing the problem of obtaining derivatives (and in general, the Taylor series) of expectation values. Borrowing ideas from the lattice field theory community, we examine two approaches. One is based on reweighting while the other represents an extension of the Hamiltonian approach typically used by the Hybrid Monte Carlo (HMC) and similar algorithms. We show that the Hamiltonian approach can be understood as a change of variables of the reweighting approach, resulting in much reduced variances of the coefficients of the Taylor series. This work opens the door to find other variance reduction techniques for derivatives of expectation values.

Sparse Implicit Processes for Approximate Inference

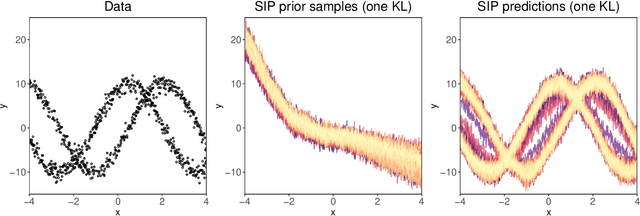
Implicit Processes (IPs) are flexible priors that can describe models such as Bayesian neural networks, neural samplers and data generators. IPs allow for approximate inference in function-space. This avoids some degenerate problems of parameter-space approximate inference due to the high number of parameters and strong dependencies. For this, an extra IP is often used to approximate the posterior of the prior IP. However, simultaneously adjusting the parameters of the prior IP and the approximate posterior IP is a challenging task. Existing methods that can tune the prior IP result in a Gaussian predictive distribution, which fails to capture important data patterns. By contrast, methods producing flexible predictive distributions by using another IP to approximate the posterior process cannot fit the prior IP to the observed data. We propose here a method that can carry out both tasks. For this, we rely on an inducing-point representation of the prior IP, as often done in the context of sparse Gaussian processes. The result is a scalable method for approximate inference with IPs that can tune the prior IP parameters to the data, and that provides accurate non-Gaussian predictive distributions.

Multi-class Gaussian Process Classification with Noisy Inputs

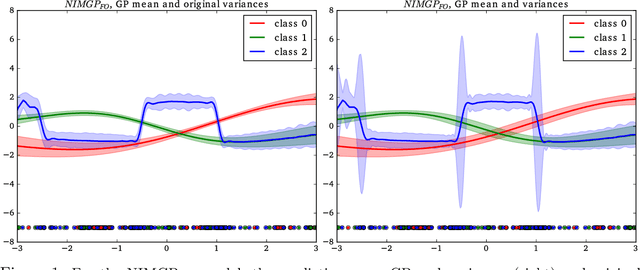
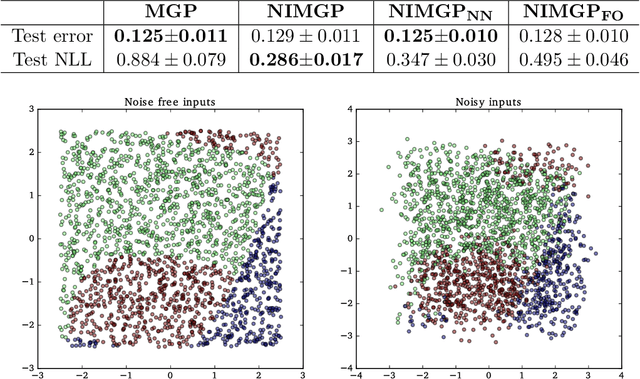
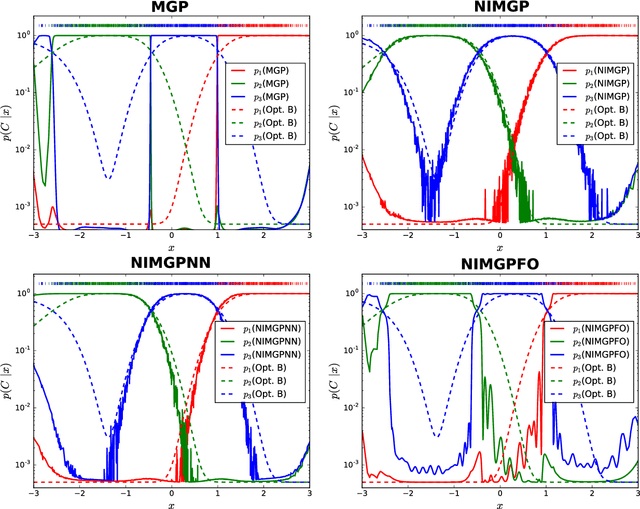
It is a common practice in the supervised machine learning community to assume that the observed data are noise-free in the input attributes. Nevertheless, scenarios with input noise are common in real problems, as measurements are never perfectly accurate. If this input noise is not taken into account, a supervised machine learning method is expected to perform sub-optimally. In this paper, we focus on multi-class classification problems and use Gaussian processes (GPs) as the underlying classifier. Motivated by a dataset coming from the astrophysics domain, we hypothesize that the observed data may contain noise in the inputs. Therefore, we devise several multi-class GP classifiers that can account for input noise. Such classifiers can be efficiently trained using variational inference to approximate the posterior distribution of the latent variables of the model. Moreover, in some situations, the amount of noise can be known before-hand. If this is the case, it can be readily introduced in the proposed methods. This prior information is expected to lead to better performance results. We have evaluated the proposed methods by carrying out several experiments, involving synthetic and real data. These data include several datasets from the UCI repository, the MNIST dataset and a dataset coming from astrophysics. The results obtained show that, although the classification error is similar across methods, the predictive distribution of the proposed methods is better, in terms of the test log-likelihood, than the predictive distribution of a classifier based on GPs that ignores input noise.