Input Dependent Sparse Gaussian Processes

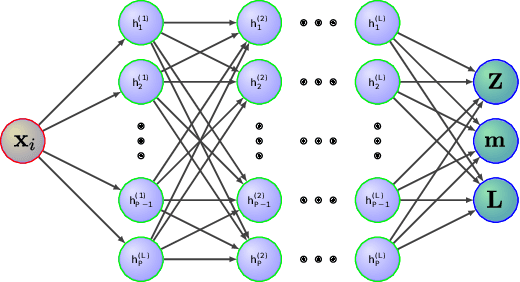
Gaussian Processes (GPs) are Bayesian models that provide uncertainty estimates associated to the predictions made. They are also very flexible due to their non-parametric nature. Nevertheless, GPs suffer from poor scalability as the number of training instances N increases. More precisely, they have a cubic cost with respect to $N$. To overcome this problem, sparse GP approximations are often used, where a set of $M \ll N$ inducing points is introduced during training. The location of the inducing points is learned by considering them as parameters of an approximate posterior distribution $q$. Sparse GPs, combined with variational inference for inferring $q$, reduce the training cost of GPs to $\mathcal{O}(M^3)$. Critically, the inducing points determine the flexibility of the model and they are often located in regions of the input space where the latent function changes. A limitation is, however, that for some learning tasks a large number of inducing points may be required to obtain a good prediction performance. To address this limitation, we propose here to amortize the computation of the inducing points locations, as well as the parameters of the variational posterior approximation q. For this, we use a neural network that receives the observed data as an input and outputs the inducing points locations and the parameters of $q$. We evaluate our method in several experiments, showing that it performs similar or better than other state-of-the-art sparse variational GP approaches. However, with our method the number of inducing points is reduced drastically due to their dependency on the input data. This makes our method scale to larger datasets and have faster training and prediction times.

Multi-class Gaussian Process Classification with Noisy Inputs

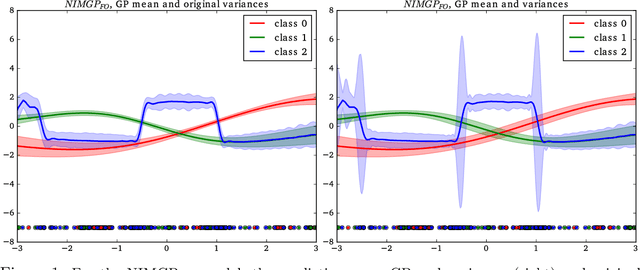
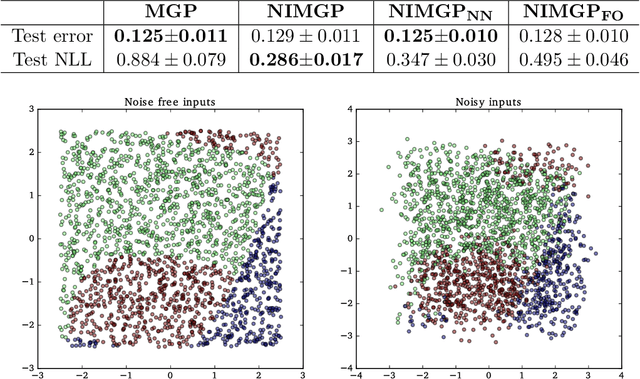
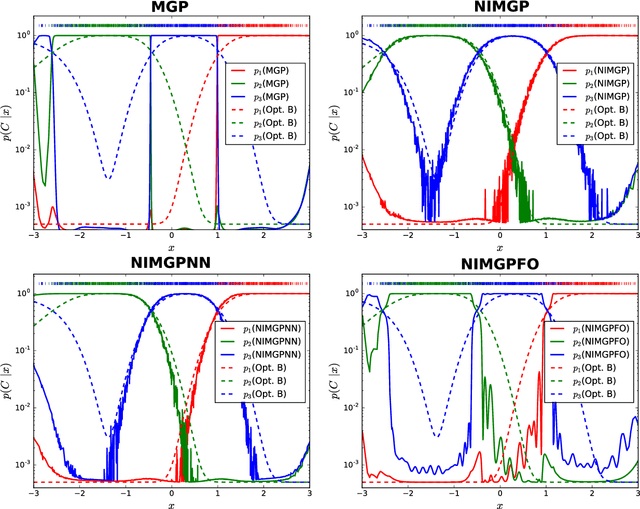
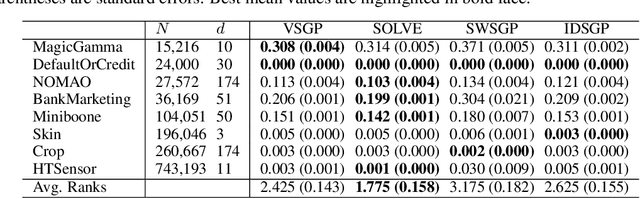
It is a common practice in the supervised machine learning community to assume that the observed data are noise-free in the input attributes. Nevertheless, scenarios with input noise are common in real problems, as measurements are never perfectly accurate. If this input noise is not taken into account, a supervised machine learning method is expected to perform sub-optimally. In this paper, we focus on multi-class classification problems and use Gaussian processes (GPs) as the underlying classifier. Motivated by a dataset coming from the astrophysics domain, we hypothesize that the observed data may contain noise in the inputs. Therefore, we devise several multi-class GP classifiers that can account for input noise. Such classifiers can be efficiently trained using variational inference to approximate the posterior distribution of the latent variables of the model. Moreover, in some situations, the amount of noise can be known before-hand. If this is the case, it can be readily introduced in the proposed methods. This prior information is expected to lead to better performance results. We have evaluated the proposed methods by carrying out several experiments, involving synthetic and real data. These data include several datasets from the UCI repository, the MNIST dataset and a dataset coming from astrophysics. The results obtained show that, although the classification error is similar across methods, the predictive distribution of the proposed methods is better, in terms of the test log-likelihood, than the predictive distribution of a classifier based on GPs that ignores input noise.

Scalable Multi-Class Gaussian Process Classification using Expectation Propagation

This paper describes an expectation propagation (EP) method for multi-class classification with Gaussian processes that scales well to very large datasets. In such a method the estimate of the log-marginal-likelihood involves a sum across the data instances. This enables efficient training using stochastic gradients and mini-batches. When this type of training is used, the computational cost does not depend on the number of data instances $N$. Furthermore, extra assumptions in the approximate inference process make the memory cost independent of $N$. The consequence is that the proposed EP method can be used on datasets with millions of instances. We compare empirically this method with alternative approaches that approximate the required computations using variational inference. The results show that it performs similar or even better than these techniques, which sometimes give significantly worse predictive distributions in terms of the test log-likelihood. Besides this, the training process of the proposed approach also seems to converge in a smaller number of iterations.