Fixed-Mean Gaussian Processes for Post-hoc Bayesian Deep Learning

Recently, there has been an increasing interest in performing post-hoc uncertainty estimation about the predictions of pre-trained deep neural networks (DNNs). Given a pre-trained DNN via back-propagation, these methods enhance the original network by adding output confidence measures, such as error bars, without compromising its initial accuracy. In this context, we introduce a novel family of sparse variational Gaussian processes (GPs), where the posterior mean is fixed to any continuous function when using a universal kernel. Specifically, we fix the mean of this GP to the output of the pre-trained DNN, allowing our approach to effectively fit the GP's predictive variances to estimate the DNN prediction uncertainty. Our approach leverages variational inference (VI) for efficient stochastic optimization, with training costs that remain independent of the number of training points, scaling efficiently to large datasets such as ImageNet. The proposed method, called fixed mean GP (FMGP), is architecture-agnostic, relying solely on the pre-trained model's outputs to adjust the predictive variances. Experimental results demonstrate that FMGP improves both uncertainty estimation and computational efficiency when compared to state-of-the-art methods.

Alpha Entropy Search for New Information-based Bayesian Optimization

Bayesian optimization (BO) methods based on information theory have obtained state-of-the-art results in several tasks. These techniques heavily rely on the Kullback-Leibler (KL) divergence to compute the acquisition function. In this work, we introduce a novel information-based class of acquisition functions for BO called Alpha Entropy Search (AES). AES is based on the {\alpha}-divergence, that generalizes the KL divergence. Iteratively, AES selects the next evaluation point as the one whose associated target value has the highest level of the dependency with respect to the location and associated value of the global maximum of the optimization problem. Dependency is measured in terms of the {\alpha}-divergence, as an alternative to the KL divergence. Intuitively, this favors the evaluation of the objective function at the most informative points about the global maximum. The {\alpha}-divergence has a free parameter {\alpha}, which determines the behavior of the divergence, trading-off evaluating differences between distributions at a single mode, and evaluating differences globally. Therefore, different values of {\alpha} result in different acquisition functions. AES acquisition lacks a closed-form expression. However, we propose an efficient and accurate approximation using a truncated Gaussian distribution. In practice, the value of {\alpha} can be chosen by the practitioner, but here we suggest to use a combination of acquisition functions obtained by simultaneously considering a range of values of {\alpha}. We provide an implementation of AES in BOTorch and we evaluate its performance in both synthetic, benchmark and real-world experiments involving the tuning of the hyper-parameters of a deep neural network. These experiments show that the performance of AES is competitive with respect to other information-based acquisition functions such as JES, MES or PES.

Deep Transformed Gaussian Processes

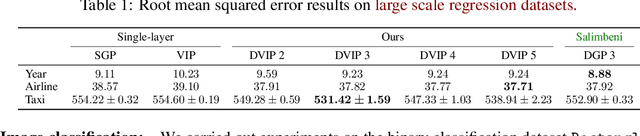
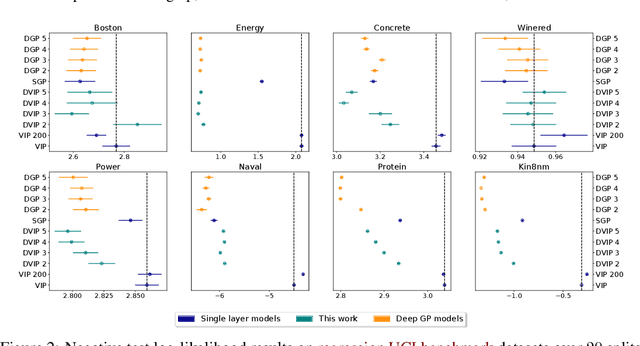
Transformed Gaussian Processes (TGPs) are stochastic processes specified by transforming samples from the joint distribution from a prior process (typically a GP) using an invertible transformation; increasing the flexibility of the base process. Furthermore, they achieve competitive results compared with Deep Gaussian Processes (DGPs), which are another generalization constructed by a hierarchical concatenation of GPs. In this work, we propose a generalization of TGPs named Deep Transformed Gaussian Processes (DTGPs), which follows the trend of concatenating layers of stochastic processes. More precisely, we obtain a multi-layer model in which each layer is a TGP. This generalization implies an increment of flexibility with respect to both TGPs and DGPs. Exact inference in such a model is intractable. However, we show that one can use variational inference to approximate the required computations yielding a straightforward extension of the popular DSVI inference algorithm Salimbeni et al (2017). The experiments conducted evaluate the proposed novel DTGPs in multiple regression datasets, achieving good scalability and performance.

Variational Linearized Laplace Approximation for Bayesian Deep Learning

Pre-trained deep neural networks can be adapted to perform uncertainty estimation by transforming them into Bayesian neural networks via methods such as Laplace approximation (LA) or its linearized form (LLA), among others. To make these methods more tractable, the generalized Gauss-Newton (GGN) approximation is often used. However, due to complex inefficiency difficulties, both LA and LLA rely on further approximations, such as Kronecker-factored or diagonal approximate GGN matrices, which can affect the results. To address these issues, we propose a new method for scaling LLA using a variational sparse Gaussian Process (GP) approximation based on the dual RKHS of GPs. Our method retains the predictive mean of the original model while allowing for efficient stochastic optimization and scalability in both the number of parameters and the size of the training dataset. Moreover, its training cost is independent of the number of training points, improving over previously existing methods. Our preliminary experiments indicate that it outperforms already existing efficient variants of LLA, such as accelerated LLA (ELLA), based on the Nystr\"om approximation.

Correcting Model Bias with Sparse Implicit Processes

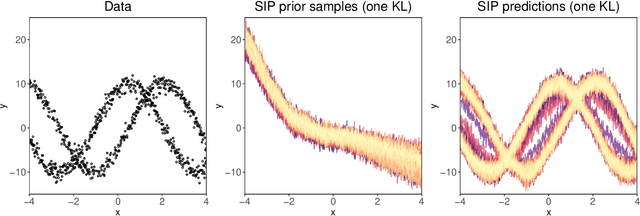
Model selection in machine learning (ML) is a crucial part of the Bayesian learning procedure. Model choice may impose strong biases on the resulting predictions, which can hinder the performance of methods such as Bayesian neural networks and neural samplers. On the other hand, newly proposed approaches for Bayesian ML exploit features of approximate inference in function space with implicit stochastic processes (a generalization of Gaussian processes). The approach of Sparse Implicit Processes (SIP) is particularly successful in this regard, since it is fully trainable and achieves flexible predictions. Here, we expand on the original experiments to show that SIP is capable of correcting model bias when the data generating mechanism differs strongly from the one implied by the model. We use synthetic datasets to show that SIP is capable of providing predictive distributions that reflect the data better than the exact predictions of the initial, but wrongly assumed model.

Deep Variational Implicit Processes

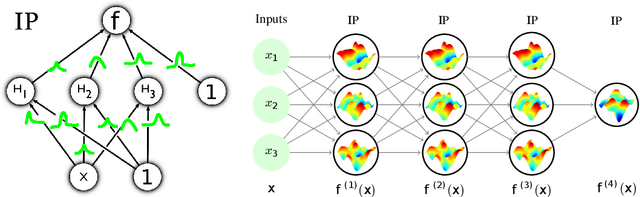
Implicit processes (IPs) are a generalization of Gaussian processes (GPs). IPs may lack a closed-form expression but are easy to sample from. Examples include, among others, Bayesian neural networks or neural samplers. IPs can be used as priors over functions, resulting in flexible models with well-calibrated prediction uncertainty estimates. Methods based on IPs usually carry out function-space approximate inference, which overcomes some of the difficulties of parameter-space approximate inference. Nevertheless, the approximations employed often limit the expressiveness of the final model, resulting, \emph{e.g.}, in a Gaussian predictive distribution, which can be restrictive. We propose here a multi-layer generalization of IPs called the Deep Variational Implicit process (DVIP). This generalization is similar to that of deep GPs over GPs, but it is more flexible due to the use of IPs as the prior distribution over the latent functions. We describe a scalable variational inference algorithm for training DVIP and show that it outperforms previous IP-based methods and also deep GPs. We support these claims via extensive regression and classification experiments. We also evaluate DVIP on large datasets with up to several million data instances to illustrate its good scalability and performance.

Efficient Transformed Gaussian Processes for Non-Stationary Dependent Multi-class Classification

This work introduces the Efficient Transformed Gaussian Process (ETGP), a new way of creating C stochastic processes characterized by: 1) the C processes are non-stationary, 2) the C processes are dependent by construction without needing a mixing matrix, 3) training and making predictions is very efficient since the number of Gaussian Processes (GP) operations (e.g. inverting the inducing point's covariance matrix) do not depend on the number of processes. This makes the ETGP particularly suited for multi-class problems with a very large number of classes, which are the problems studied in this work. ETGPs exploit the recently proposed Transformed Gaussian Process (TGP), a stochastic process specified by transforming a Gaussian Process using an invertible transformation. However, unlike TGPs, ETGPs are constructed by transforming a single sample from a GP using C invertible transformations. We derive an efficient sparse variational inference algorithm for the proposed model and demonstrate its utility in 5 classification tasks which include low/medium/large datasets and a different number of classes, ranging from just a few to hundreds. Our results show that ETGPs, in general, outperform state-of-the-art methods for multi-class classification based on GPs, and have a lower computational cost (around one order of magnitude smaller).

Gaussian Processes for Missing Value Imputation

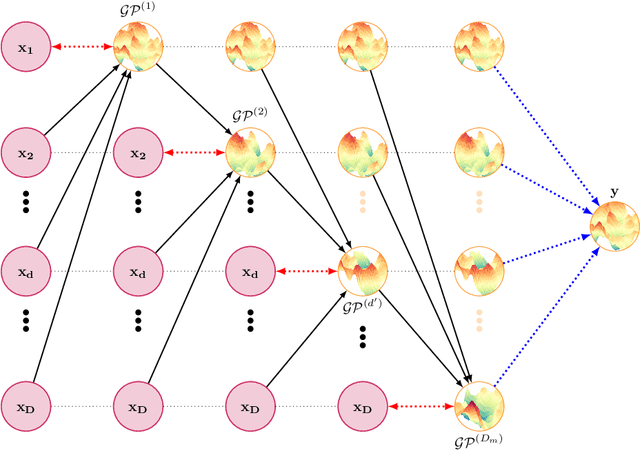
Missing values are common in many real-life datasets. However, most of the current machine learning methods can not handle missing values. This means that they should be imputed beforehand. Gaussian Processes (GPs) are non-parametric models with accurate uncertainty estimates that combined with sparse approximations and stochastic variational inference scale to large data sets. Sparse GPs can be used to compute a predictive distribution for missing data. Here, we present a hierarchical composition of sparse GPs that is used to predict missing values at each dimension using all the variables from the other dimensions. We call the approach missing GP (MGP). MGP can be trained simultaneously to impute all observed missing values. Specifically, it outputs a predictive distribution for each missing value that is then used in the imputation of other missing values. We evaluate MGP in one private clinical data set and four UCI datasets with a different percentage of missing values. We compare the performance of MGP with other state-of-the-art methods for imputing missing values, including variants based on sparse GPs and deep GPs. The results obtained show a significantly better performance of MGP.

Inference over radiative transfer models using variational and expectation maximization methods

Earth observation from satellites offers the possibility to monitor our planet with unprecedented accuracy. Radiative transfer models (RTMs) encode the energy transfer through the atmosphere, and are used to model and understand the Earth system, as well as to estimate the parameters that describe the status of the Earth from satellite observations by inverse modeling. However, performing inference over such simulators is a challenging problem. RTMs are nonlinear, non-differentiable and computationally costly codes, which adds a high level of difficulty in inference. In this paper, we introduce two computational techniques to infer not only point estimates of biophysical parameters but also their joint distribution. One of them is based on a variational autoencoder approach and the second one is based on a Monte Carlo Expectation Maximization (MCEM) scheme. We compare and discuss benefits and drawbacks of each approach. We also provide numerical comparisons in synthetic simulations and the real PROSAIL model, a popular RTM that combines land vegetation leaf and canopy modeling. We analyze the performance of the two approaches for modeling and inferring the distribution of three key biophysical parameters for quantifying the terrestrial biosphere.

Sparse Implicit Processes for Approximate Inference

Implicit Processes (IPs) are flexible priors that can describe models such as Bayesian neural networks, neural samplers and data generators. IPs allow for approximate inference in function-space. This avoids some degenerate problems of parameter-space approximate inference due to the high number of parameters and strong dependencies. For this, an extra IP is often used to approximate the posterior of the prior IP. However, simultaneously adjusting the parameters of the prior IP and the approximate posterior IP is a challenging task. Existing methods that can tune the prior IP result in a Gaussian predictive distribution, which fails to capture important data patterns. By contrast, methods producing flexible predictive distributions by using another IP to approximate the posterior process cannot fit the prior IP to the observed data. We propose here a method that can carry out both tasks. For this, we rely on an inducing-point representation of the prior IP, as often done in the context of sparse Gaussian processes. The result is a scalable method for approximate inference with IPs that can tune the prior IP parameters to the data, and that provides accurate non-Gaussian predictive distributions.