Alpha Entropy Search for New Information-based Bayesian Optimization

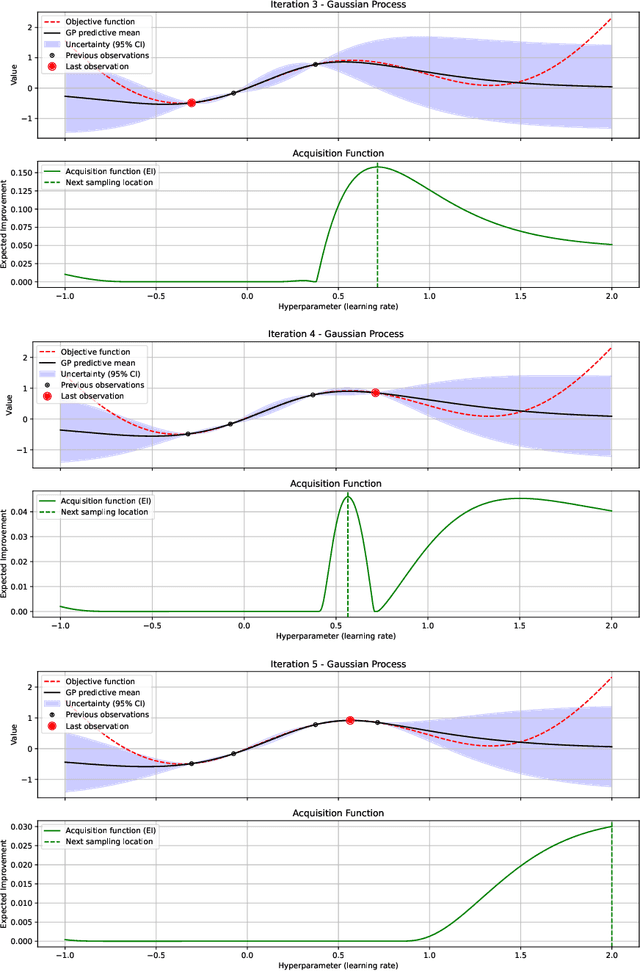
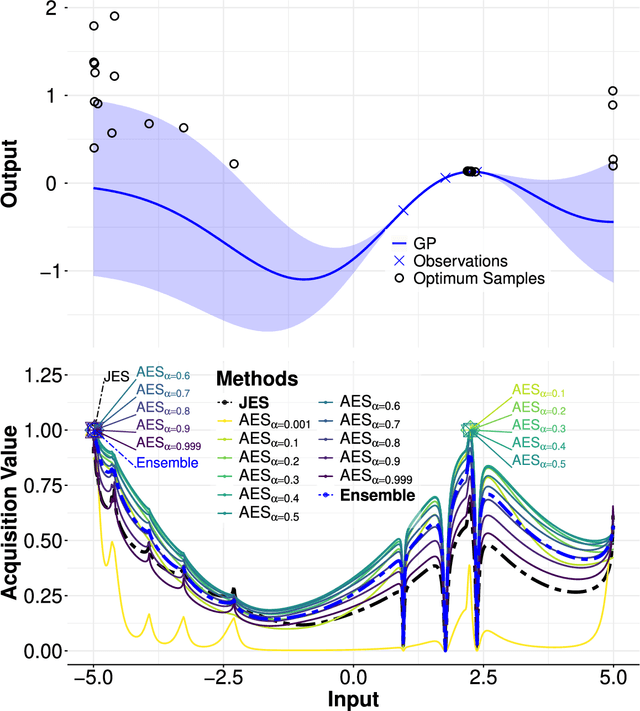
Bayesian optimization (BO) methods based on information theory have obtained state-of-the-art results in several tasks. These techniques heavily rely on the Kullback-Leibler (KL) divergence to compute the acquisition function. In this work, we introduce a novel information-based class of acquisition functions for BO called Alpha Entropy Search (AES). AES is based on the {\alpha}-divergence, that generalizes the KL divergence. Iteratively, AES selects the next evaluation point as the one whose associated target value has the highest level of the dependency with respect to the location and associated value of the global maximum of the optimization problem. Dependency is measured in terms of the {\alpha}-divergence, as an alternative to the KL divergence. Intuitively, this favors the evaluation of the objective function at the most informative points about the global maximum. The {\alpha}-divergence has a free parameter {\alpha}, which determines the behavior of the divergence, trading-off evaluating differences between distributions at a single mode, and evaluating differences globally. Therefore, different values of {\alpha} result in different acquisition functions. AES acquisition lacks a closed-form expression. However, we propose an efficient and accurate approximation using a truncated Gaussian distribution. In practice, the value of {\alpha} can be chosen by the practitioner, but here we suggest to use a combination of acquisition functions obtained by simultaneously considering a range of values of {\alpha}. We provide an implementation of AES in BOTorch and we evaluate its performance in both synthetic, benchmark and real-world experiments involving the tuning of the hyper-parameters of a deep neural network. These experiments show that the performance of AES is competitive with respect to other information-based acquisition functions such as JES, MES or PES.

Max-value Entropy Search for Multi-objective Bayesian Optimization with Constraints

We present MESMOC, a Bayesian optimization method that can be used to solve constrained multi-objective problems when the objectives and the constraints are expensive to evaluate. MESMOC works by minimizing the entropy of the solution of the optimization problem in function space, i.e., the Pareto frontier, to guide the search for the optimum. The execution cost of MESMOC is linear in the number of objectives and constraints. Furthermore, it is often significantly smaller than the cost of alternative methods based on minimizing the entropy of the Pareto set. The reason for this is that it is easier to approximate the required computations in MESMOC. Moreover, MESMOC's acquisition function is expressed as the sum of one acquisition per each black-box (objective or constraint). Thus, it can be used in a decoupled evaluation setting in which one chooses not only the next input location to evaluate, but also which black-box to evaluate there. We compare MESMOC with related methods in synthetic and real optimization problems. These experiments show that MESMOC is competitive with other information-based methods for constrained multi-objective Bayesian optimization, but its execution time is smaller.