Inference over radiative transfer models using variational and expectation maximization methods

Earth observation from satellites offers the possibility to monitor our planet with unprecedented accuracy. Radiative transfer models (RTMs) encode the energy transfer through the atmosphere, and are used to model and understand the Earth system, as well as to estimate the parameters that describe the status of the Earth from satellite observations by inverse modeling. However, performing inference over such simulators is a challenging problem. RTMs are nonlinear, non-differentiable and computationally costly codes, which adds a high level of difficulty in inference. In this paper, we introduce two computational techniques to infer not only point estimates of biophysical parameters but also their joint distribution. One of them is based on a variational autoencoder approach and the second one is based on a Monte Carlo Expectation Maximization (MCEM) scheme. We compare and discuss benefits and drawbacks of each approach. We also provide numerical comparisons in synthetic simulations and the real PROSAIL model, a popular RTM that combines land vegetation leaf and canopy modeling. We analyze the performance of the two approaches for modeling and inferring the distribution of three key biophysical parameters for quantifying the terrestrial biosphere.

Integrating Domain Knowledge in Data-driven Earth Observation with Process Convolutions

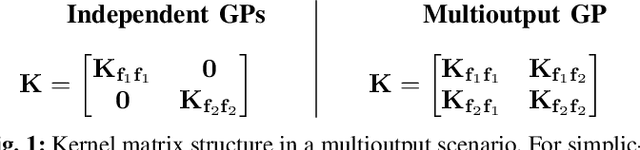
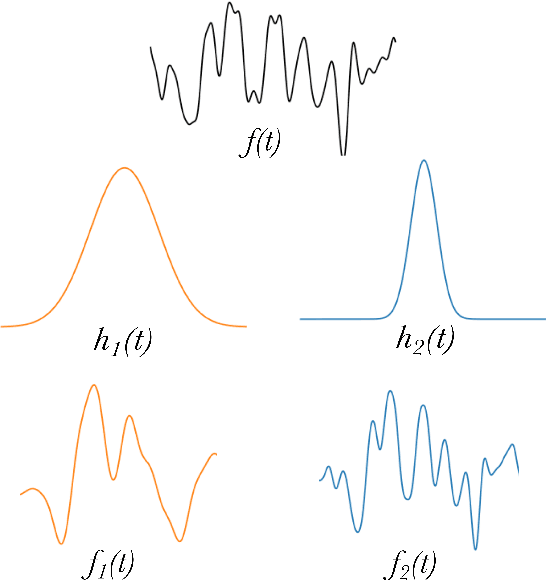
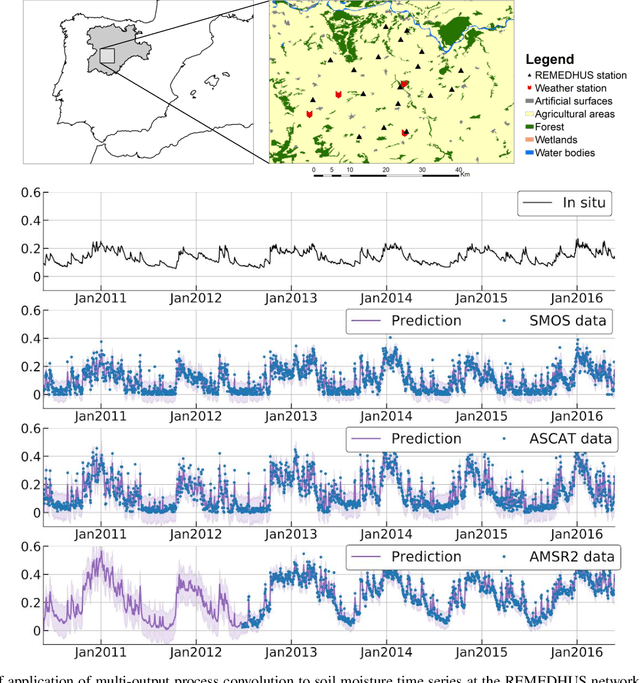
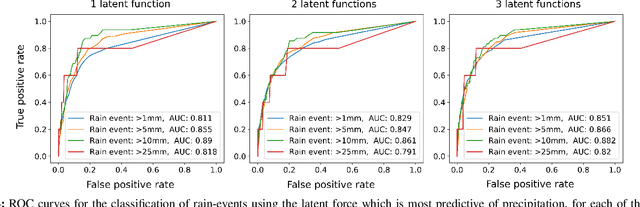
The modelling of Earth observation data is a challenging problem, typically approached by either purely mechanistic or purely data-driven methods. Mechanistic models encode the domain knowledge and physical rules governing the system. Such models, however, need the correct specification of all interactions between variables in the problem and the appropriate parameterization is a challenge in itself. On the other hand, machine learning approaches are flexible data-driven tools, able to approximate arbitrarily complex functions, but lack interpretability and struggle when data is scarce or in extrapolation regimes. In this paper, we argue that hybrid learning schemes that combine both approaches can address all these issues efficiently. We introduce Gaussian process (GP) convolution models for hybrid modelling in Earth observation (EO) problems. We specifically propose the use of a class of GP convolution models called latent force models (LFMs) for EO time series modelling, analysis and understanding. LFMs are hybrid models that incorporate physical knowledge encoded in differential equations into a multioutput GP model. LFMs can transfer information across time-series, cope with missing observations, infer explicit latent functions forcing the system, and learn parameterizations which are very helpful for system analysis and interpretability. We consider time series of soil moisture from active (ASCAT) and passive (SMOS, AMSR2) microwave satellites. We show how assuming a first order differential equation as governing equation, the model automatically estimates the e-folding time or decay rate related to soil moisture persistence and discovers latent forces related to precipitation. The proposed hybrid methodology reconciles the two main approaches in remote sensing parameter estimation by blending statistical learning and mechanistic modeling.

Deep Gaussian Processes for Biogeophysical Parameter Retrieval and Model Inversion

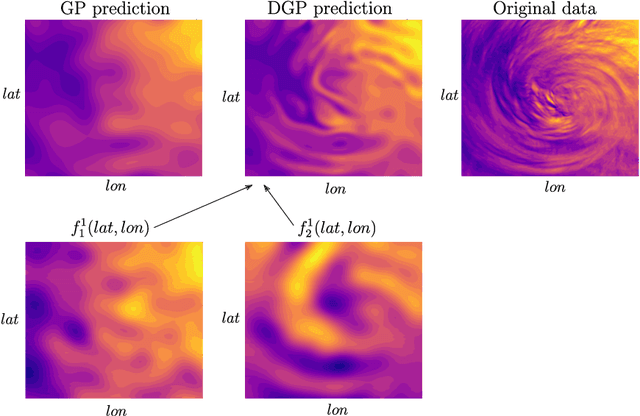
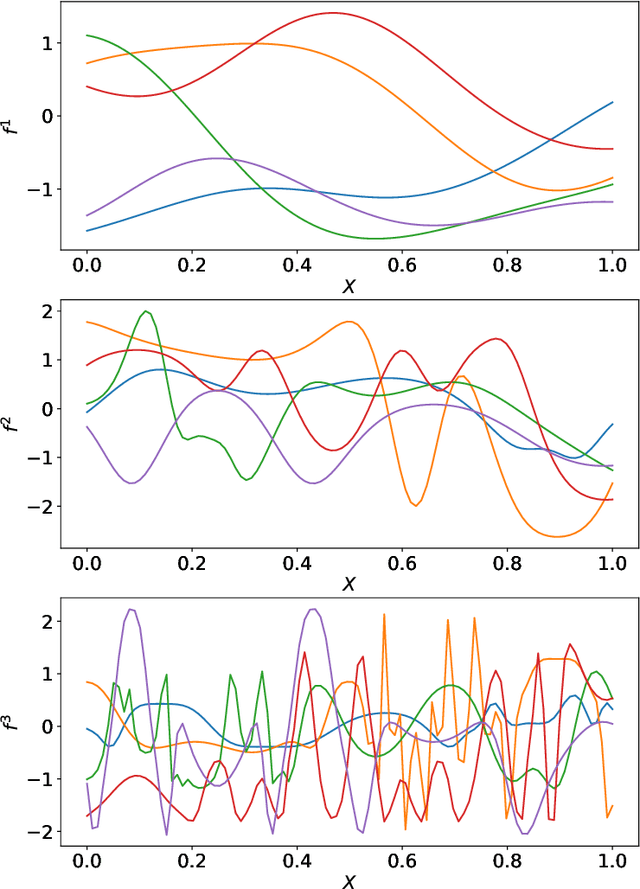
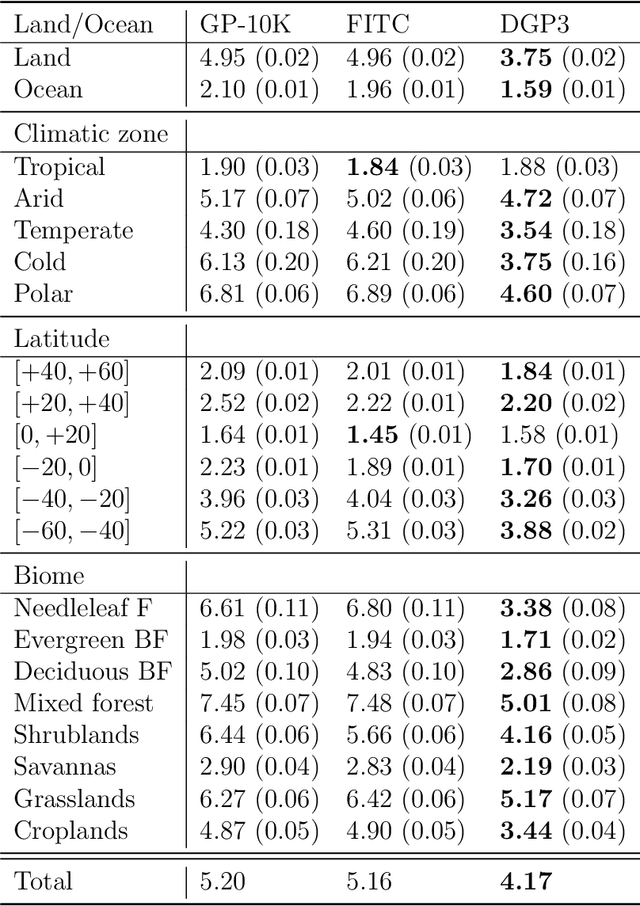
Parameter retrieval and model inversion are key problems in remote sensing and Earth observation. Currently, different approximations exist: a direct, yet costly, inversion of radiative transfer models (RTMs); the statistical inversion with in situ data that often results in problems with extrapolation outside the study area; and the most widely adopted hybrid modeling by which statistical models, mostly nonlinear and non-parametric machine learning algorithms, are applied to invert RTM simulations. We will focus on the latter. Among the different existing algorithms, in the last decade kernel based methods, and Gaussian Processes (GPs) in particular, have provided useful and informative solutions to such RTM inversion problems. This is in large part due to the confidence intervals they provide, and their predictive accuracy. However, RTMs are very complex, highly nonlinear, and typically hierarchical models, so that often a shallow GP model cannot capture complex feature relations for inversion. This motivates the use of deeper hierarchical architectures, while still preserving the desirable properties of GPs. This paper introduces the use of deep Gaussian Processes (DGPs) for bio-geo-physical model inversion. Unlike shallow GP models, DGPs account for complicated (modular, hierarchical) processes, provide an efficient solution that scales well to big datasets, and improve prediction accuracy over their single layer counterpart. In the experimental section, we provide empirical evidence of performance for the estimation of surface temperature and dew point temperature from infrared sounding data, as well as for the prediction of chlorophyll content, inorganic suspended matter, and coloured dissolved matter from multispectral data acquired by the Sentinel-3 OLCI sensor. The presented methodology allows for more expressive forms of GPs in remote sensing model inversion problems.

Deep Gaussian Processes for geophysical parameter retrieval

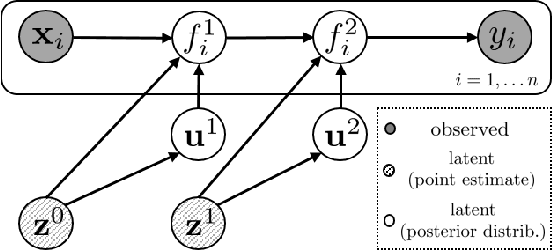
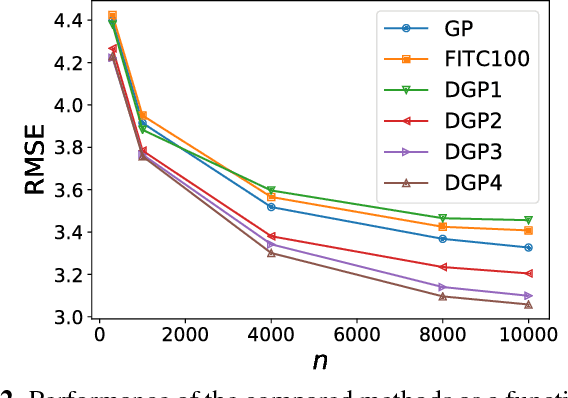
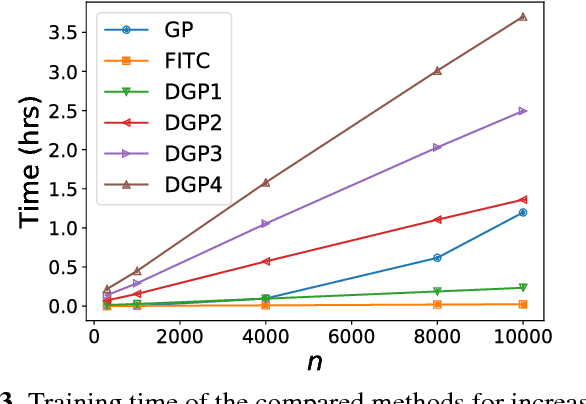
This paper introduces deep Gaussian processes (DGPs) for geophysical parameter retrieval. Unlike the standard full GP model, the DGP accounts for complicated (modular, hierarchical) processes, provides an efficient solution that scales well to large datasets, and improves prediction accuracy over standard full and sparse GP models. We give empirical evidence of performance for estimation of surface dew point temperature from infrared sounding data.

Active emulation of computer codes with Gaussian processes -- Application to remote sensing

Many fields of science and engineering rely on running simulations with complex and computationally expensive models to understand the involved processes in the system of interest. Nevertheless, the high cost involved hamper reliable and exhaustive simulations. Very often such codes incorporate heuristics that ironically make them less tractable and transparent. This paper introduces an active learning methodology for adaptively constructing surrogate models, i.e. emulators, of such costly computer codes in a multi-output setting. The proposed technique is sequential and adaptive, and is based on the optimization of a suitable acquisition function. It aims to achieve accurate approximations, model tractability, as well as compact and expressive simulated datasets. In order to achieve this, the proposed Active Multi-Output Gaussian Process Emulator (AMOGAPE) combines the predictive capacity of Gaussian Processes (GPs) with the design of an acquisition function that favors sampling in low density and fluctuating regions of the approximation functions. Comparing different acquisition functions, we illustrate the promising performance of the method for the construction of emulators with toy examples, as well as for a widely used remote sensing transfer code.

Joint Gaussian Processes for Biophysical Parameter Retrieval

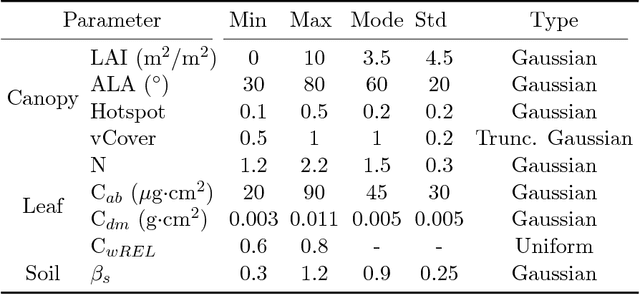
Solving inverse problems is central to geosciences and remote sensing. Radiative transfer models (RTMs) represent mathematically the physical laws which govern the phenomena in remote sensing applications (forward models). The numerical inversion of the RTM equations is a challenging and computationally demanding problem, and for this reason, often the application of a nonlinear statistical regression is preferred. In general, regression models predict the biophysical parameter of interest from the corresponding received radiance. However, this approach does not employ the physical information encoded in the RTMs. An alternative strategy, which attempts to include the physical knowledge, consists in learning a regression model trained using data simulated by an RTM code. In this work, we introduce a nonlinear nonparametric regression model which combines the benefits of the two aforementioned approaches. The inversion is performed taking into account jointly both real observations and RTM-simulated data. The proposed Joint Gaussian Process (JGP) provides a solid framework for exploiting the regularities between the two types of data. The JGP automatically detects the relative quality of the simulated and real data, and combines them accordingly. This occurs by learning an additional hyper-parameter w.r.t. a standard GP model, and fitting parameters through maximizing the pseudo-likelihood of the real observations. The resulting scheme is both simple and robust, i.e., capable of adapting to different scenarios. The advantages of the JGP method compared to benchmark strategies are shown considering RTM-simulated and real observations in different experiments. Specifically, we consider leaf area index (LAI) retrieval from Landsat data combined with simulated data generated by the PROSAIL model.