Integrating Domain Knowledge in Data-driven Earth Observation with Process Convolutions

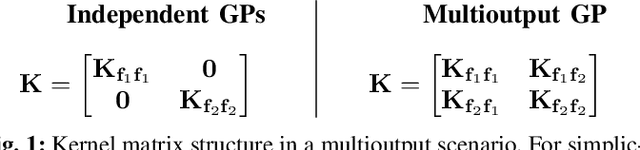
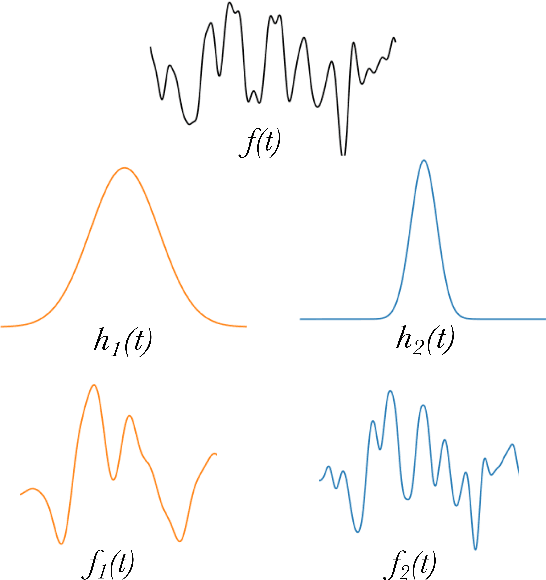
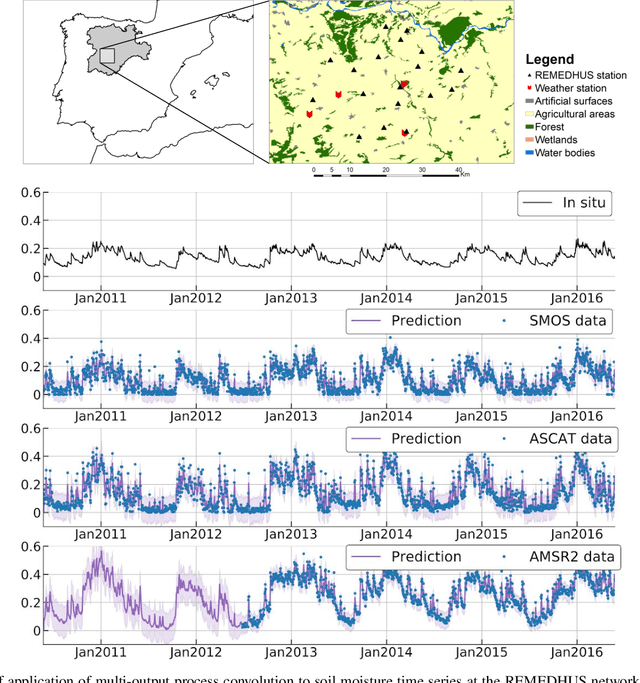
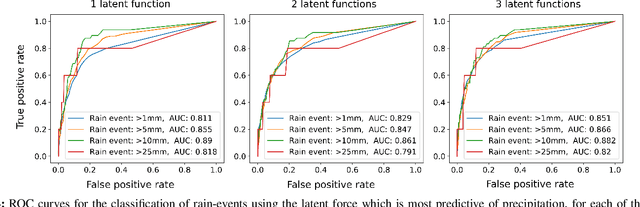
The modelling of Earth observation data is a challenging problem, typically approached by either purely mechanistic or purely data-driven methods. Mechanistic models encode the domain knowledge and physical rules governing the system. Such models, however, need the correct specification of all interactions between variables in the problem and the appropriate parameterization is a challenge in itself. On the other hand, machine learning approaches are flexible data-driven tools, able to approximate arbitrarily complex functions, but lack interpretability and struggle when data is scarce or in extrapolation regimes. In this paper, we argue that hybrid learning schemes that combine both approaches can address all these issues efficiently. We introduce Gaussian process (GP) convolution models for hybrid modelling in Earth observation (EO) problems. We specifically propose the use of a class of GP convolution models called latent force models (LFMs) for EO time series modelling, analysis and understanding. LFMs are hybrid models that incorporate physical knowledge encoded in differential equations into a multioutput GP model. LFMs can transfer information across time-series, cope with missing observations, infer explicit latent functions forcing the system, and learn parameterizations which are very helpful for system analysis and interpretability. We consider time series of soil moisture from active (ASCAT) and passive (SMOS, AMSR2) microwave satellites. We show how assuming a first order differential equation as governing equation, the model automatically estimates the e-folding time or decay rate related to soil moisture persistence and discovers latent forces related to precipitation. The proposed hybrid methodology reconciles the two main approaches in remote sensing parameter estimation by blending statistical learning and mechanistic modeling.