Causal machine learning for sustainable agroecosystems

In a changing climate, sustainable agriculture is essential for food security and environmental health. However, it is challenging to understand the complex interactions among its biophysical, social, and economic components. Predictive machine learning (ML), with its capacity to learn from data, is leveraged in sustainable agriculture for applications like yield prediction and weather forecasting. Nevertheless, it cannot explain causal mechanisms and remains descriptive rather than prescriptive. To address this gap, we propose causal ML, which merges ML's data processing with causality's ability to reason about change. This facilitates quantifying intervention impacts for evidence-based decision-making and enhances predictive model robustness. We showcase causal ML through eight diverse applications that benefit stakeholders across the agri-food chain, including farmers, policymakers, and researchers.

Integrating Domain Knowledge in Data-driven Earth Observation with Process Convolutions

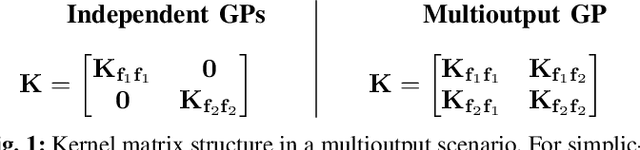
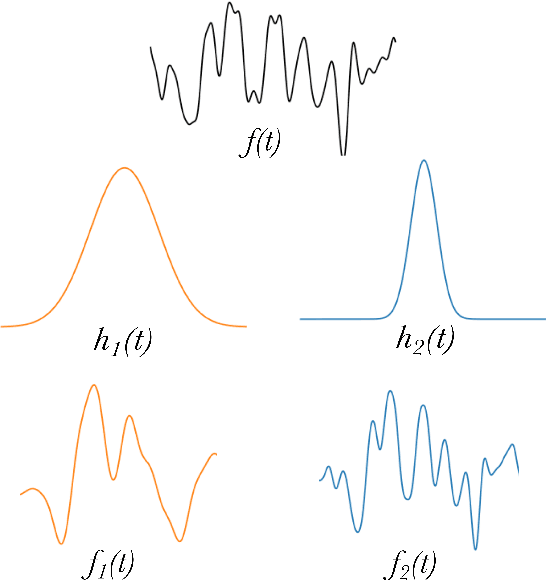
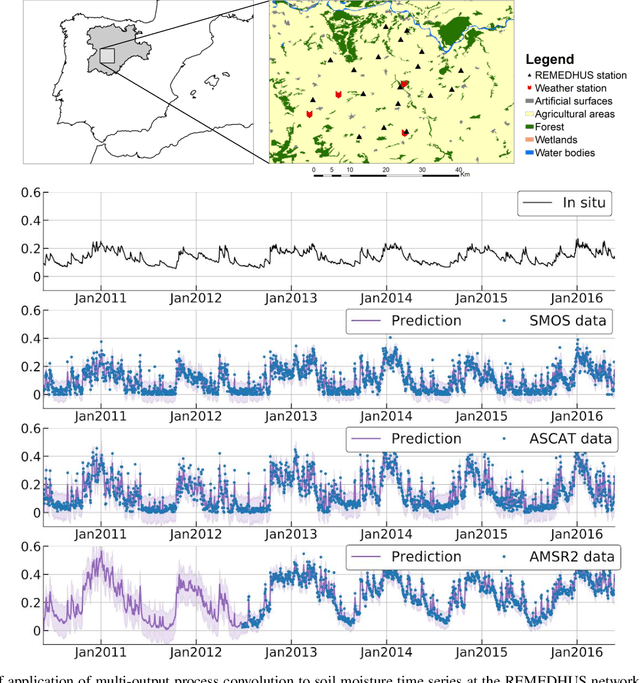
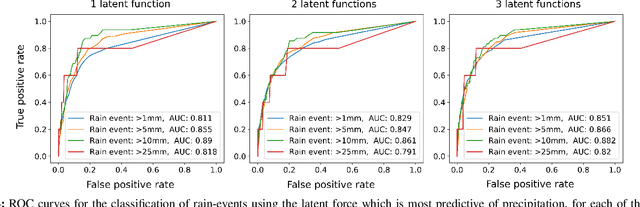
The modelling of Earth observation data is a challenging problem, typically approached by either purely mechanistic or purely data-driven methods. Mechanistic models encode the domain knowledge and physical rules governing the system. Such models, however, need the correct specification of all interactions between variables in the problem and the appropriate parameterization is a challenge in itself. On the other hand, machine learning approaches are flexible data-driven tools, able to approximate arbitrarily complex functions, but lack interpretability and struggle when data is scarce or in extrapolation regimes. In this paper, we argue that hybrid learning schemes that combine both approaches can address all these issues efficiently. We introduce Gaussian process (GP) convolution models for hybrid modelling in Earth observation (EO) problems. We specifically propose the use of a class of GP convolution models called latent force models (LFMs) for EO time series modelling, analysis and understanding. LFMs are hybrid models that incorporate physical knowledge encoded in differential equations into a multioutput GP model. LFMs can transfer information across time-series, cope with missing observations, infer explicit latent functions forcing the system, and learn parameterizations which are very helpful for system analysis and interpretability. We consider time series of soil moisture from active (ASCAT) and passive (SMOS, AMSR2) microwave satellites. We show how assuming a first order differential equation as governing equation, the model automatically estimates the e-folding time or decay rate related to soil moisture persistence and discovers latent forces related to precipitation. The proposed hybrid methodology reconciles the two main approaches in remote sensing parameter estimation by blending statistical learning and mechanistic modeling.

Nonlinear Distribution Regression for Remote Sensing Applications

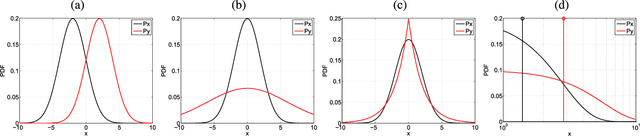
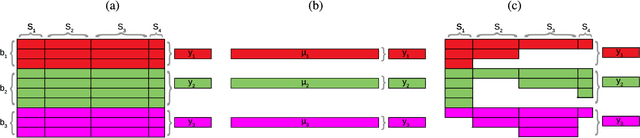
In many remote sensing applications one wants to estimate variables or parameters of interest from observations. When the target variable is available at a resolution that matches the remote sensing observations, standard algorithms such as neural networks, random forests or Gaussian processes are readily available to relate the two. However, we often encounter situations where the target variable is only available at the group level, i.e. collectively associated to a number of remotely sensed observations. This problem setting is known in statistics and machine learning as {\em multiple instance learning} or {\em distribution regression}. This paper introduces a nonlinear (kernel-based) method for distribution regression that solves the previous problems without making any assumption on the statistics of the grouped data. The presented formulation considers distribution embeddings in reproducing kernel Hilbert spaces, and performs standard least squares regression with the empirical means therein. A flexible version to deal with multisource data of different dimensionality and sample sizes is also presented and evaluated. It allows working with the native spatial resolution of each sensor, avoiding the need of match-up procedures. Noting the large computational cost of the approach, we introduce an efficient version via random Fourier features to cope with millions of points and groups.

Understanding Climate Impacts on Vegetation with Gaussian Processes in Granger Causality

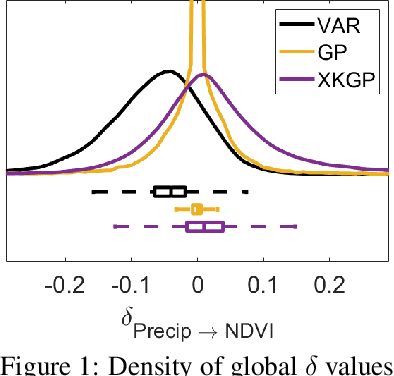
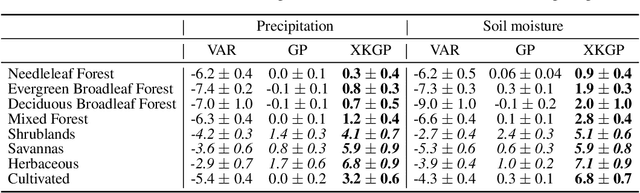
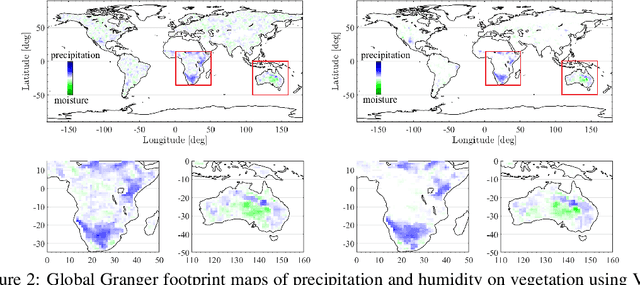
Global warming is leading to unprecedented changes in our planet, with great societal, economical and environmental implications, especially with the growing demand of biofuels and food. Assessing the impact of climate on vegetation is of pressing need. We approached the attribution problem with a novel nonlinear Granger causal (GC) methodology and used a large data archive of remote sensing satellite products, environmental and climatic variables spatio-temporally gridded over more than 30 years. We generalize kernel Granger causality by considering the variables cross-relations explicitly in Hilbert spaces, and use the covariance in Gaussian processes. The method generalizes the linear and kernel GC methods, and comes with tighter bounds of performance based on Rademacher complexity. Spatially-explicit global Granger footprints of precipitation and soil moisture on vegetation greenness are identified more sharply than previous GC methods.

Living in the Physics and Machine Learning Interplay for Earth Observation

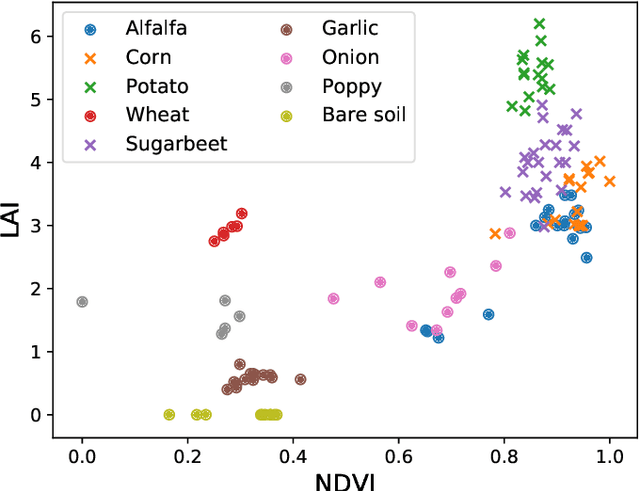
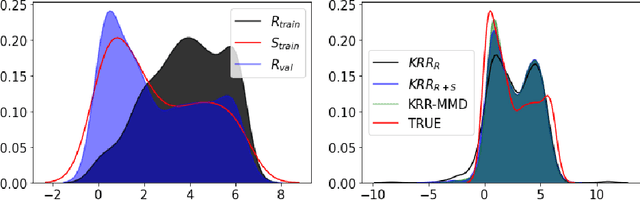
Most problems in Earth sciences aim to do inferences about the system, where accurate predictions are just a tiny part of the whole problem. Inferences mean understanding variables relations, deriving models that are physically interpretable, that are simple parsimonious, and mathematically tractable. Machine learning models alone are excellent approximators, but very often do not respect the most elementary laws of physics, like mass or energy conservation, so consistency and confidence are compromised. In this paper, we describe the main challenges ahead in the field, and introduce several ways to live in the Physics and machine learning interplay: to encode differential equations from data, constrain data-driven models with physics-priors and dependence constraints, improve parameterizations, emulate physical models, and blend data-driven and process-based models. This is a collective long-term AI agenda towards developing and applying algorithms capable of discovering knowledge in the Earth system.

Gaussianizing the Earth: Multidimensional Information Measures for Earth Data Analysis

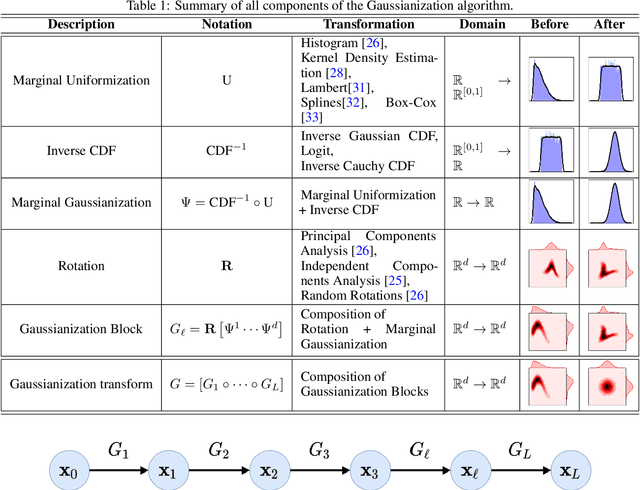
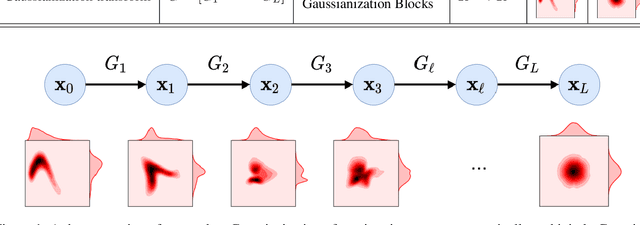
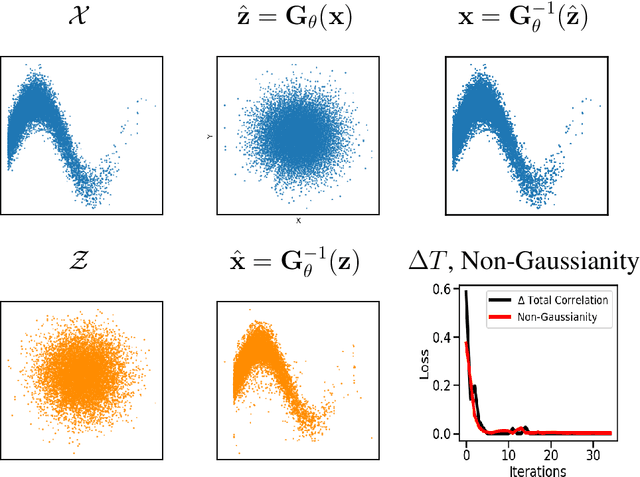
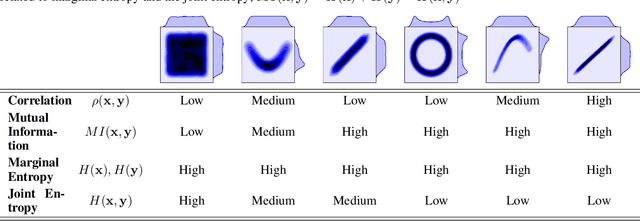
Information theory is an excellent framework for analyzing Earth system data because it allows us to characterize uncertainty and redundancy, and is universally interpretable. However, accurately estimating information content is challenging because spatio-temporal data is high-dimensional, heterogeneous and has non-linear characteristics. In this paper, we apply multivariate Gaussianization for probability density estimation which is robust to dimensionality, comes with statistical guarantees, and is easy to apply. In addition, this methodology allows us to estimate information-theoretic measures to characterize multivariate densities: information, entropy, total correlation, and mutual information. We demonstrate how information theory measures can be applied in various Earth system data analysis problems. First we show how the method can be used to jointly Gaussianize radar backscattering intensities, synthesize hyperspectral data, and quantify of information content in aerial optical images. We also quantify the information content of several variables describing the soil-vegetation status in agro-ecosystems, and investigate the temporal scales that maximize their shared information under extreme events such as droughts. Finally, we measure the relative information content of space and time dimensions in remote sensing products and model simulations involving long records of key variables such as precipitation, sensible heat and evaporation. Results confirm the validity of the method, for which we anticipate a wide use and adoption. Code and demos of the implemented algorithms and information-theory measures are provided.