Nonlinear Distribution Regression for Remote Sensing Applications

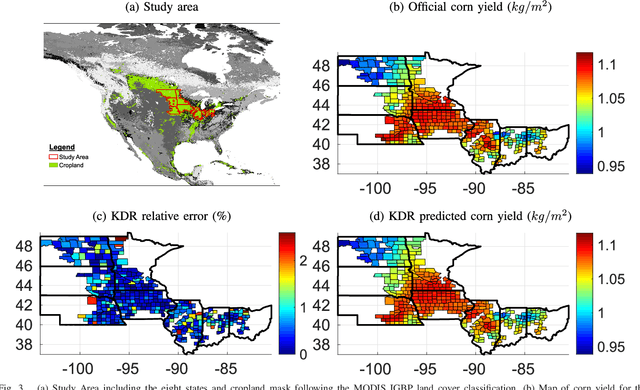
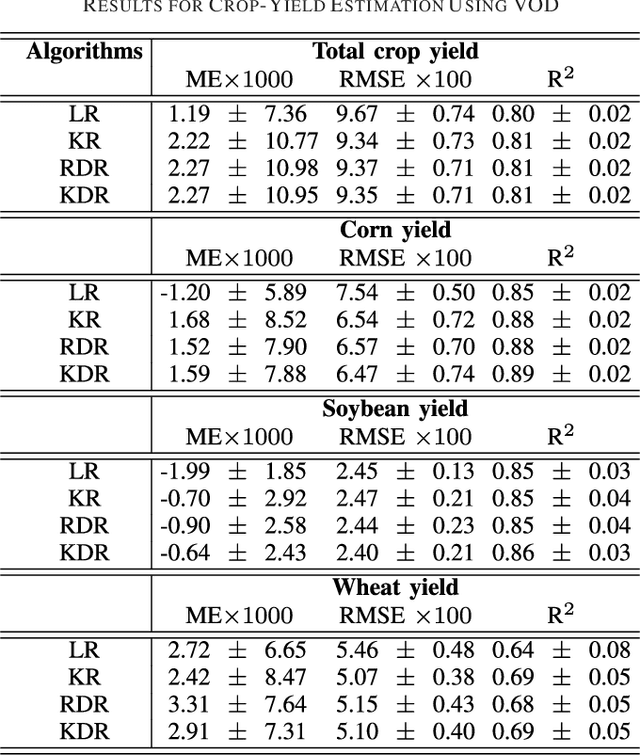
In many remote sensing applications one wants to estimate variables or parameters of interest from observations. When the target variable is available at a resolution that matches the remote sensing observations, standard algorithms such as neural networks, random forests or Gaussian processes are readily available to relate the two. However, we often encounter situations where the target variable is only available at the group level, i.e. collectively associated to a number of remotely sensed observations. This problem setting is known in statistics and machine learning as {\em multiple instance learning} or {\em distribution regression}. This paper introduces a nonlinear (kernel-based) method for distribution regression that solves the previous problems without making any assumption on the statistics of the grouped data. The presented formulation considers distribution embeddings in reproducing kernel Hilbert spaces, and performs standard least squares regression with the empirical means therein. A flexible version to deal with multisource data of different dimensionality and sample sizes is also presented and evaluated. It allows working with the native spatial resolution of each sensor, avoiding the need of match-up procedures. Noting the large computational cost of the approach, we introduce an efficient version via random Fourier features to cope with millions of points and groups.