A Classification of Artificial Intelligence Systems for Mathematics Education

This chapter provides an overview of the different Artificial Intelligence (AI) systems that are being used in contemporary digital tools for Mathematics Education (ME). It is aimed at researchers in AI and Machine Learning (ML), for whom we shed some light on the specific technologies that are being used in educational applications; and at researchers in ME, for whom we clarify: i) what the possibilities of the current AI technologies are, ii) what is still out of reach and iii) what is to be expected in the near future. We start our analysis by establishing a high-level taxonomy of AI tools that are found as components in digital ME applications. Then, we describe in detail how these AI tools, and in particular ML, are being used in two key applications, specifically AI-based calculators and intelligent tutoring systems. We finish the chapter with a discussion about student modeling systems and their relationship to artificial general intelligence.

Warped Gaussian Processes in Remote Sensing Parameter Estimation and Causal Inference

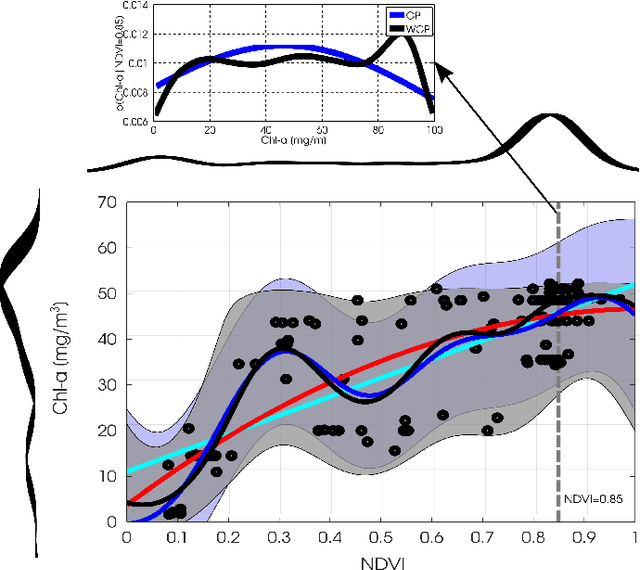
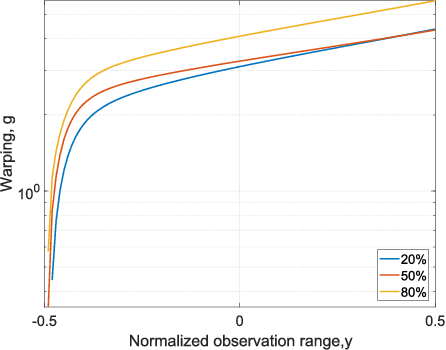
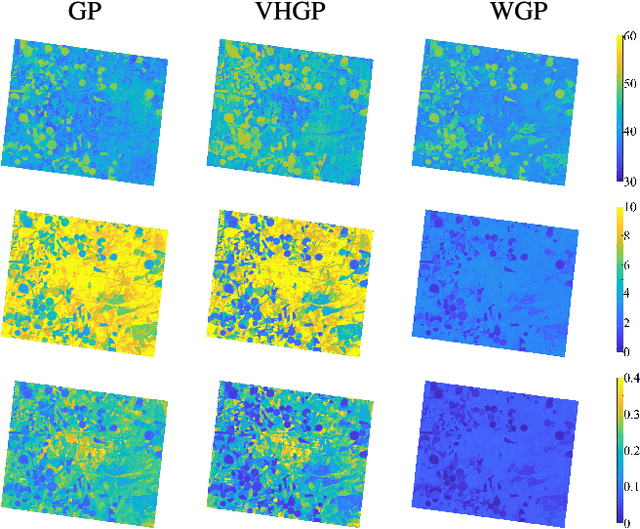
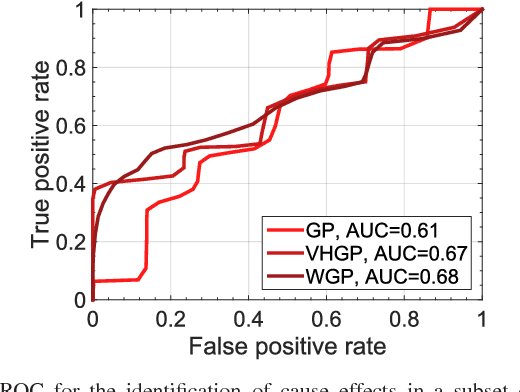
This paper introduces warped Gaussian processes (WGP) regression in remote sensing applications. WGP models output observations as a parametric nonlinear transformation of a GP. The parameters of such prior model are then learned via standard maximum likelihood. We show the good performance of the proposed model for the estimation of oceanic chlorophyll content from multispectral data, vegetation parameters (chlorophyll, leaf area index, and fractional vegetation cover) from hyperspectral data, and in the detection of the causal direction in a collection of 28 bivariate geoscience and remote sensing causal problems. The model consistently performs better than the standard GP and the more advanced heteroscedastic GP model, both in terms of accuracy and more sensible confidence intervals.

Consistent regression of biophysical parameters with kernel methods

This paper introduces a novel statistical regression framework that allows the incorporation of consistency constraints. A linear and nonlinear (kernel-based) formulation are introduced, and both imply closed-form analytical solutions. The models exploit all the information from a set of drivers while being maximally independent of a set of auxiliary, protected variables. We successfully illustrate the performance in the estimation of chlorophyll content.

Randomized RX for target detection

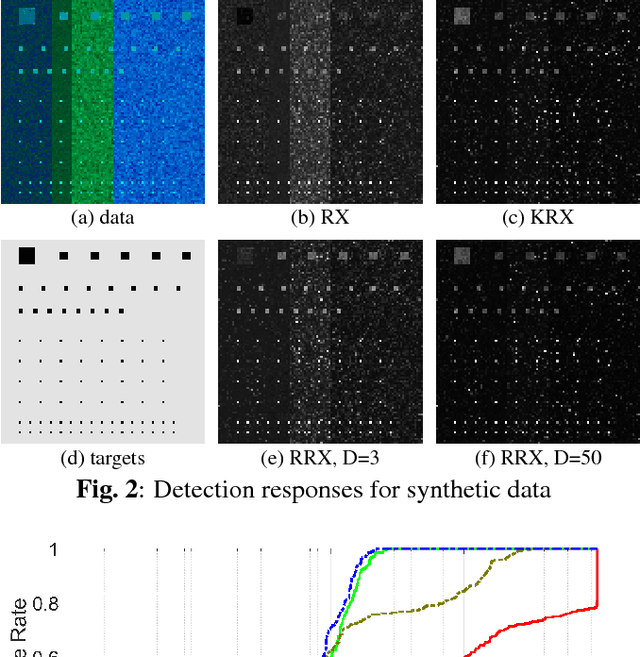
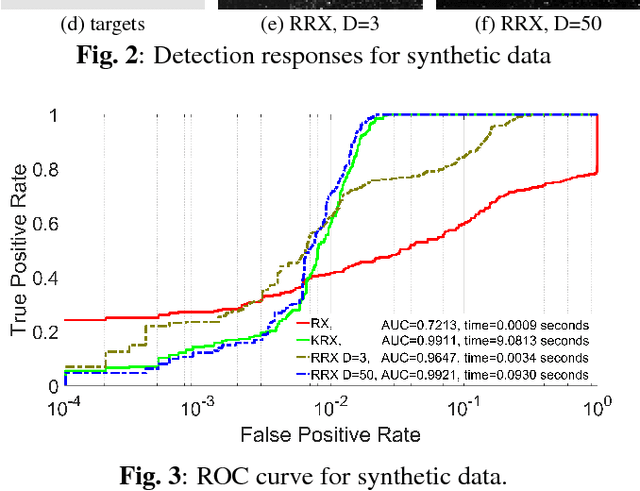
This work tackles the target detection problem through the well-known global RX method. The RX method models the clutter as a multivariate Gaussian distribution, and has been extended to nonlinear distributions using kernel methods. While the kernel RX can cope with complex clutters, it requires a considerable amount of computational resources as the number of clutter pixels gets larger. Here we propose random Fourier features to approximate the Gaussian kernel in kernel RX and consequently our development keep the accuracy of the nonlinearity while reducing the computational cost which is now controlled by an hyperparameter. Results over both synthetic and real-world image target detection problems show space and time efficiency of the proposed method while providing high detection performance.

Nonlinear Cook distance for Anomalous Change Detection

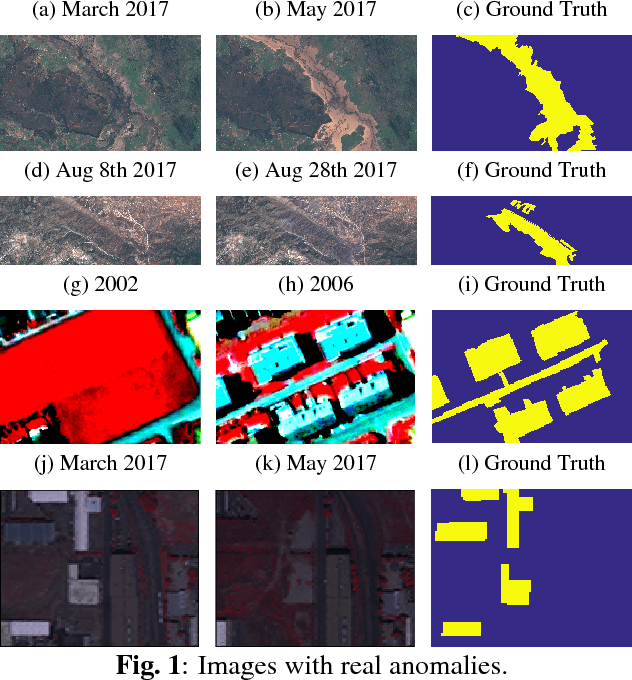
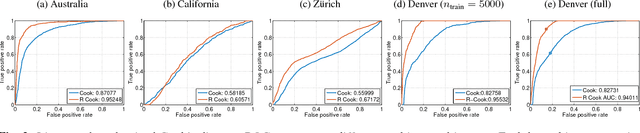
In this work we propose a method to find anomalous changes in remote sensing images based on the chronochrome approach. A regressor between images is used to discover the most {\em influential points} in the observed data. Typically, the pixels with largest residuals are decided to be anomalous changes. In order to find the anomalous pixels we consider the Cook distance and propose its nonlinear extension using random Fourier features as an efficient nonlinear measure of impact. Good empirical performance is shown over different multispectral images both visually and quantitatively evaluated with ROC curves.

Pattern Recognition Scheme for Large-Scale Cloud Detection over Landmarks

Landmark recognition and matching is a critical step in many Image Navigation and Registration (INR) models for geostationary satellite services, as well as to maintain the geometric quality assessment (GQA) in the instrument data processing chain of Earth observation satellites. Matching the landmark accurately is of paramount relevance, and the process can be strongly impacted by the cloud contamination of a given landmark. This paper introduces a complete pattern recognition methodology able to detect the presence of clouds over landmarks using Meteosat Second Generation (MSG) data. The methodology is based on the ensemble combination of dedicated support vector machines (SVMs) dependent on the particular landmark and illumination conditions. This divide-and-conquer strategy is motivated by the data complexity and follows a physically-based strategy that considers variability both in seasonality and illumination conditions along the day to split observations. In addition, it allows training the classification scheme with millions of samples at an affordable computational costs. The image archive was composed of 200 landmark test sites with near 7 million multispectral images that correspond to MSG acquisitions during 2010. Results are analyzed in terms of cloud detection accuracy and computational cost. We provide illustrative source code and a portion of the huge training data to the community.

Causal Inference in Geoscience and Remote Sensing from Observational Data

Establishing causal relations between random variables from observational data is perhaps the most important challenge in today's \blue{science}. In remote sensing and geosciences this is of special relevance to better understand the Earth's system and the complex interactions between the governing processes. In this paper, we focus on observational causal inference, thus we try to estimate the correct direction of causation using a finite set of empirical data. In addition, we focus on the more complex bivariate scenario that requires strong assumptions and no conditional independence tests can be used. In particular, we explore the framework of (non-deterministic) additive noise models, which relies on the principle of independence between the cause and the generating mechanism. A practical algorithmic instantiation of such principle only requires 1) two regression models in the forward and backward directions, and 2) the estimation of {\em statistical independence} between the obtained residuals and the observations. The direction leading to more independent residuals is decided to be the cause. We instead propose a criterion that uses the {\em sensitivity} (derivative) of the dependence estimator, the sensitivity criterion allows to identify samples most affecting the dependence measure, and hence the criterion is robust to spurious detections. We illustrate performance in a collection of 28 geoscience causal inference problems, in a database of radiative transfer models simulations and machine learning emulators in vegetation parameter modeling involving 182 problems, and in assessing the impact of different regression models in a carbon cycle problem. The criterion achieves state-of-the-art detection rates in all cases, it is generally robust to noise sources and distortions.

Nonlinear Distribution Regression for Remote Sensing Applications

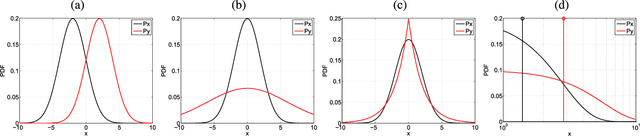
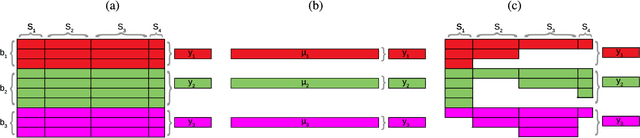
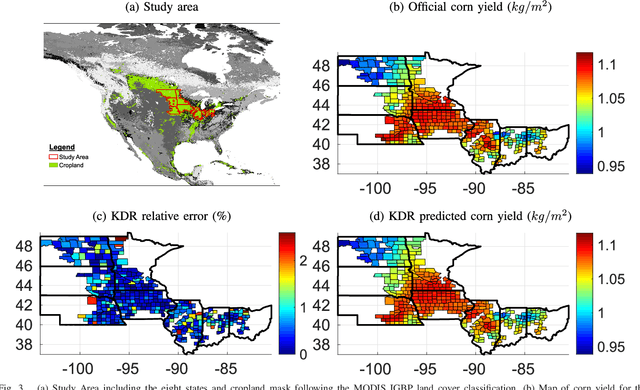
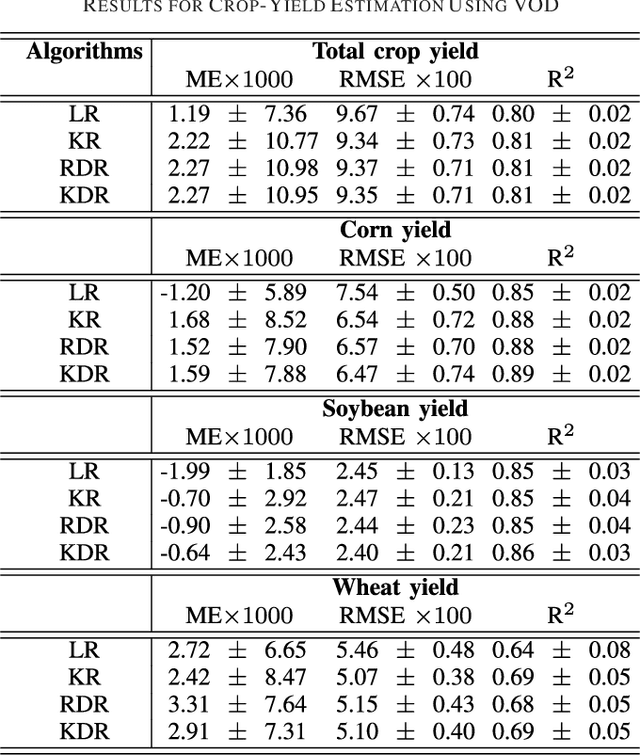
In many remote sensing applications one wants to estimate variables or parameters of interest from observations. When the target variable is available at a resolution that matches the remote sensing observations, standard algorithms such as neural networks, random forests or Gaussian processes are readily available to relate the two. However, we often encounter situations where the target variable is only available at the group level, i.e. collectively associated to a number of remotely sensed observations. This problem setting is known in statistics and machine learning as {\em multiple instance learning} or {\em distribution regression}. This paper introduces a nonlinear (kernel-based) method for distribution regression that solves the previous problems without making any assumption on the statistics of the grouped data. The presented formulation considers distribution embeddings in reproducing kernel Hilbert spaces, and performs standard least squares regression with the empirical means therein. A flexible version to deal with multisource data of different dimensionality and sample sizes is also presented and evaluated. It allows working with the native spatial resolution of each sensor, avoiding the need of match-up procedures. Noting the large computational cost of the approach, we introduce an efficient version via random Fourier features to cope with millions of points and groups.

Efficient Nonlinear RX Anomaly Detectors

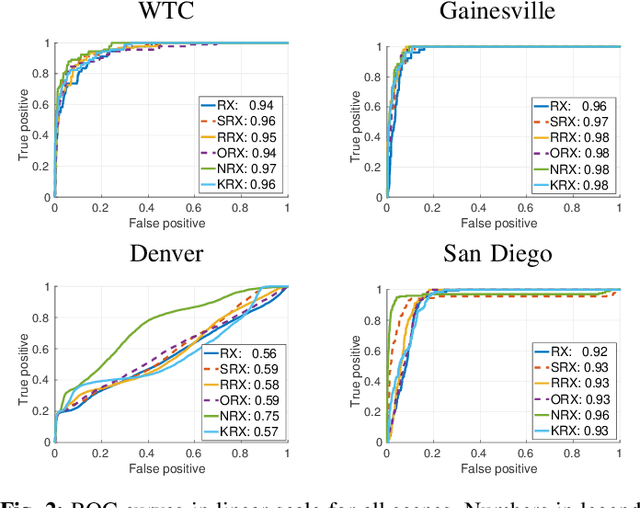
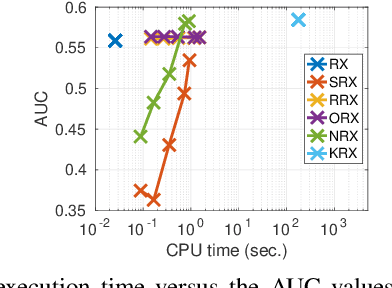
Current anomaly detection algorithms are typically challenged by either accuracy or efficiency. More accurate nonlinear detectors are typically slow and not scalable. In this letter, we propose two families of techniques to improve the efficiency of the standard kernel Reed-Xiaoli (RX) method for anomaly detection by approximating the kernel function with either {\em data-independent} random Fourier features or {\em data-dependent} basis with the Nystr\"om approach. We compare all methods for both real multi- and hyperspectral images. We show that the proposed efficient methods have a lower computational cost and they perform similar (or outperform) the standard kernel RX algorithm thanks to their implicit regularization effect. Last but not least, the Nystr\"om approach has an improved power of detection.

Causal Inference in Geosciences with Kernel Sensitivity Maps

Establishing causal relations between random variables from observational data is perhaps the most important challenge in today's Science. In remote sensing and geosciences this is of special relevance to better understand the Earth's system and the complex and elusive interactions between processes. In this paper we explore a framework to derive cause-effect relations from pairs of variables via regression and dependence estimation. We propose to focus on the sensitivity (curvature) of the dependence estimator to account for the asymmetry of the forward and inverse densities of approximation residuals. Results in a large collection of 28 geoscience causal inference problems demonstrate the good capabilities of the method.