Warped Gaussian Processes in Remote Sensing Parameter Estimation and Causal Inference
Paper and Code
Dec 09, 2020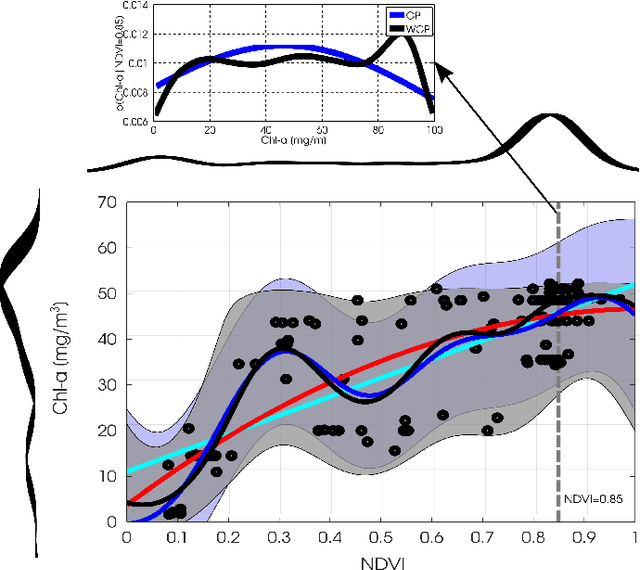
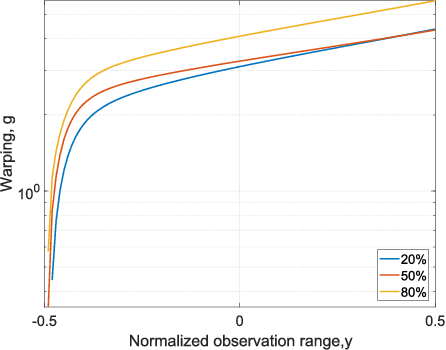
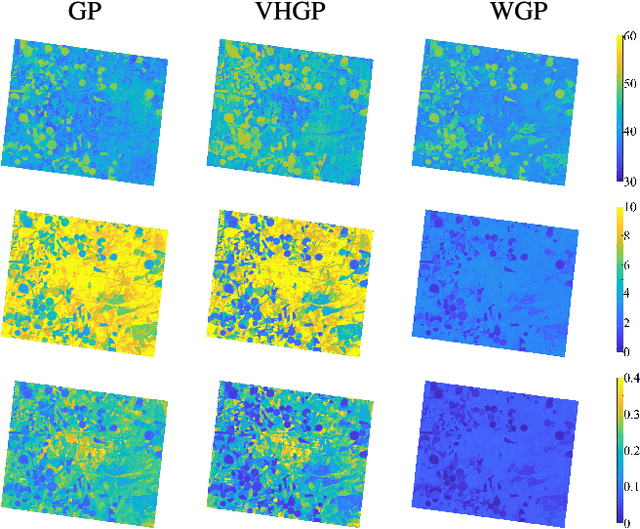
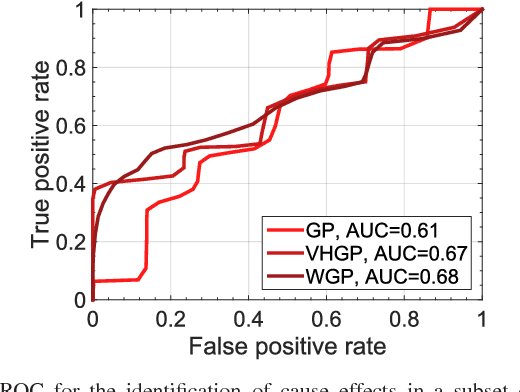
This paper introduces warped Gaussian processes (WGP) regression in remote sensing applications. WGP models output observations as a parametric nonlinear transformation of a GP. The parameters of such prior model are then learned via standard maximum likelihood. We show the good performance of the proposed model for the estimation of oceanic chlorophyll content from multispectral data, vegetation parameters (chlorophyll, leaf area index, and fractional vegetation cover) from hyperspectral data, and in the detection of the causal direction in a collection of 28 bivariate geoscience and remote sensing causal problems. The model consistently performs better than the standard GP and the more advanced heteroscedastic GP model, both in terms of accuracy and more sensible confidence intervals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge