Gap Filling of Biophysical Parameter Time Series with Multi-Output Gaussian Processes

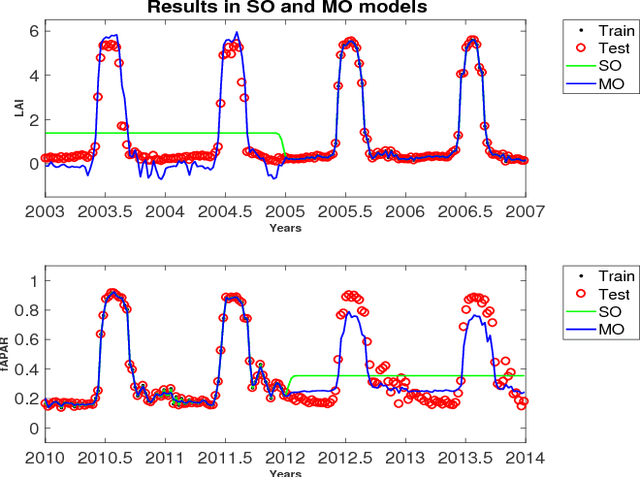
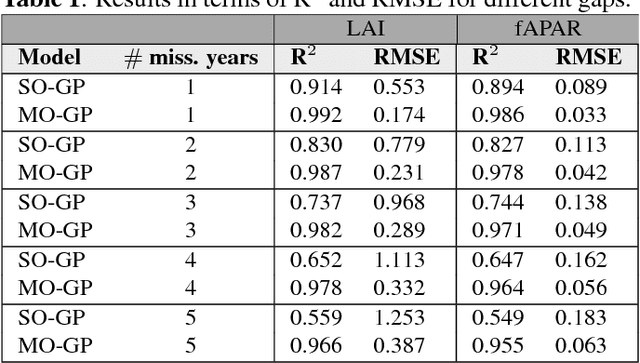
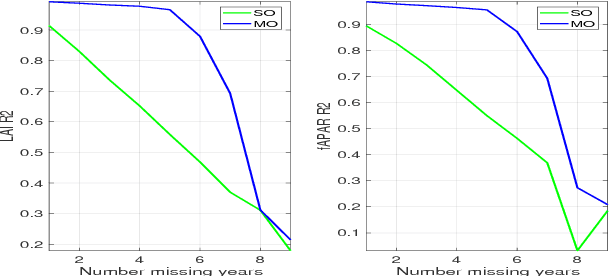
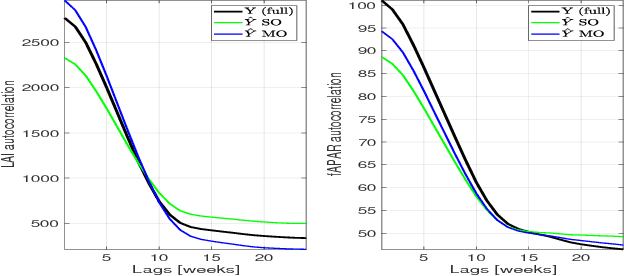
In this work we evaluate multi-output (MO) Gaussian Process (GP) models based on the linear model of coregionalization (LMC) for estimation of biophysical parameter variables under a gap filling setup. In particular, we focus on LAI and fAPAR over rice areas. We show how this problem cannot be solved with standard single-output (SO) GP models, and how the proposed MO-GP models are able to successfully predict these variables even in high missing data regimes, by implicitly performing an across-domain information transfer.

Warped Gaussian Processes in Remote Sensing Parameter Estimation and Causal Inference

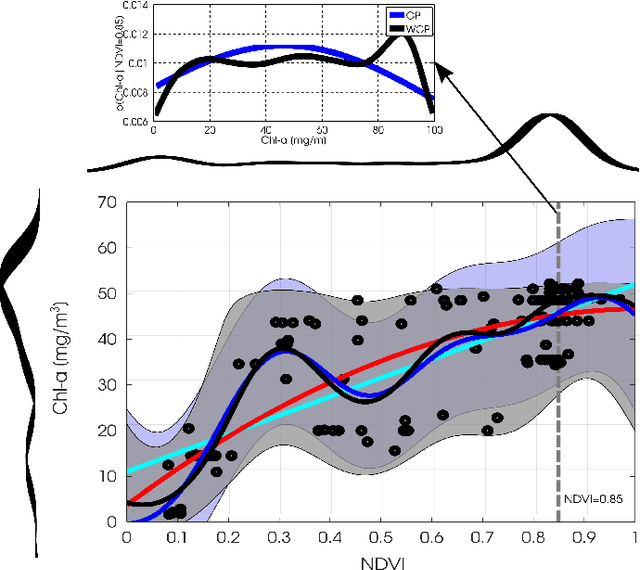
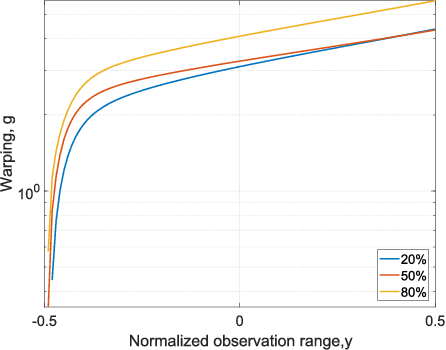
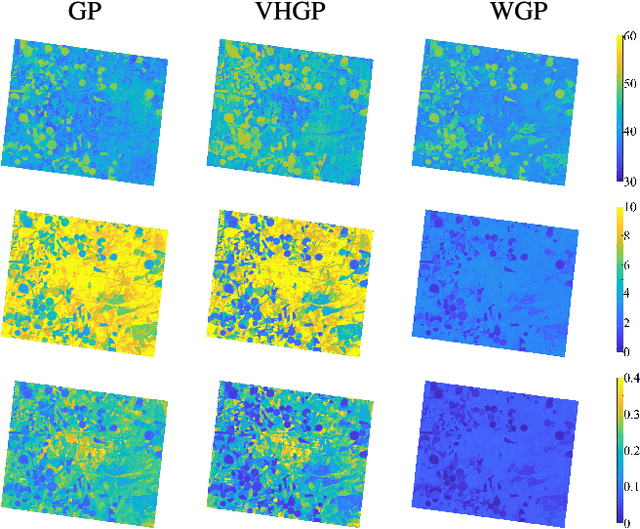
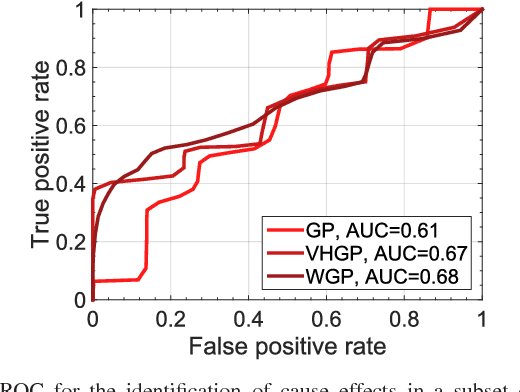
This paper introduces warped Gaussian processes (WGP) regression in remote sensing applications. WGP models output observations as a parametric nonlinear transformation of a GP. The parameters of such prior model are then learned via standard maximum likelihood. We show the good performance of the proposed model for the estimation of oceanic chlorophyll content from multispectral data, vegetation parameters (chlorophyll, leaf area index, and fractional vegetation cover) from hyperspectral data, and in the detection of the causal direction in a collection of 28 bivariate geoscience and remote sensing causal problems. The model consistently performs better than the standard GP and the more advanced heteroscedastic GP model, both in terms of accuracy and more sensible confidence intervals.

Nonlinear Distribution Regression for Remote Sensing Applications

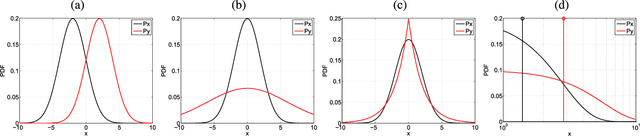
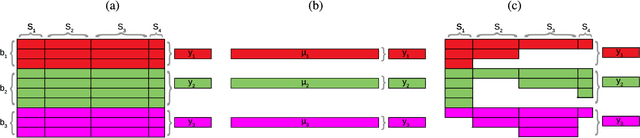
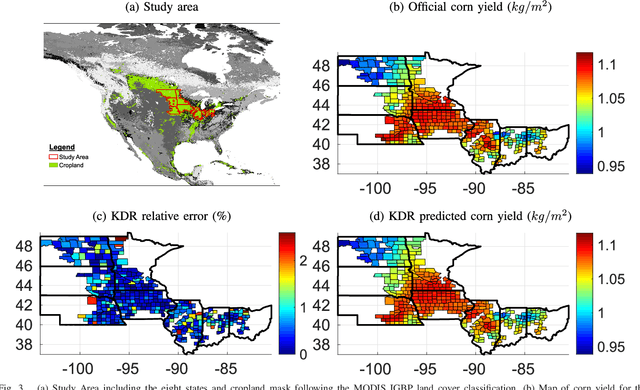
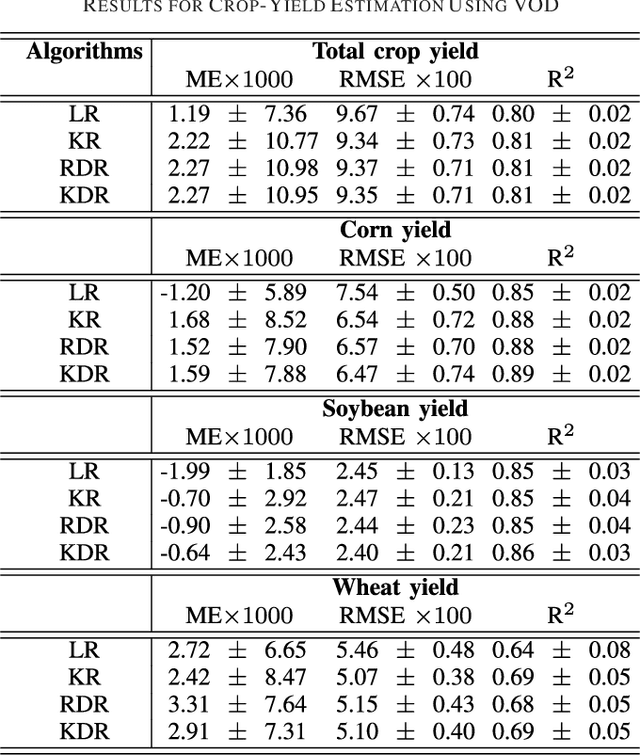
In many remote sensing applications one wants to estimate variables or parameters of interest from observations. When the target variable is available at a resolution that matches the remote sensing observations, standard algorithms such as neural networks, random forests or Gaussian processes are readily available to relate the two. However, we often encounter situations where the target variable is only available at the group level, i.e. collectively associated to a number of remotely sensed observations. This problem setting is known in statistics and machine learning as {\em multiple instance learning} or {\em distribution regression}. This paper introduces a nonlinear (kernel-based) method for distribution regression that solves the previous problems without making any assumption on the statistics of the grouped data. The presented formulation considers distribution embeddings in reproducing kernel Hilbert spaces, and performs standard least squares regression with the empirical means therein. A flexible version to deal with multisource data of different dimensionality and sample sizes is also presented and evaluated. It allows working with the native spatial resolution of each sensor, avoiding the need of match-up procedures. Noting the large computational cost of the approach, we introduce an efficient version via random Fourier features to cope with millions of points and groups.