SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

OceanBench: The Sea Surface Height Edition

The ocean profoundly influences human activities and plays a critical role in climate regulation. Our understanding has improved over the last decades with the advent of satellite remote sensing data, allowing us to capture essential quantities over the globe, e.g., sea surface height (SSH). However, ocean satellite data presents challenges for information extraction due to their sparsity and irregular sampling, signal complexity, and noise. Machine learning (ML) techniques have demonstrated their capabilities in dealing with large-scale, complex signals. Therefore we see an opportunity for ML models to harness the information contained in ocean satellite data. However, data representation and relevant evaluation metrics can be the defining factors when determining the success of applied ML. The processing steps from the raw observation data to a ML-ready state and from model outputs to interpretable quantities require domain expertise, which can be a significant barrier to entry for ML researchers. OceanBench is a unifying framework that provides standardized processing steps that comply with domain-expert standards. It provides plug-and-play data and pre-configured pipelines for ML researchers to benchmark their models and a transparent configurable framework for researchers to customize and extend the pipeline for their tasks. In this work, we demonstrate the OceanBench framework through a first edition dedicated to SSH interpolation challenges. We provide datasets and ML-ready benchmarking pipelines for the long-standing problem of interpolating observations from simulated ocean satellite data, multi-modal and multi-sensor fusion issues, and transfer-learning to real ocean satellite observations. The OceanBench framework is available at github.com/jejjohnson/oceanbench and the dataset registry is available at github.com/quentinf00/oceanbench-data-registry.

Neural Fields for Fast and Scalable Interpolation of Geophysical Ocean Variables

Optimal Interpolation (OI) is a widely used, highly trusted algorithm for interpolation and reconstruction problems in geosciences. With the influx of more satellite missions, we have access to more and more observations and it is becoming more pertinent to take advantage of these observations in applications such as forecasting and reanalysis. With the increase in the volume of available data, scalability remains an issue for standard OI and it prevents many practitioners from effectively and efficiently taking advantage of these large sums of data to learn the model hyperparameters. In this work, we leverage recent advances in Neural Fields (NerFs) as an alternative to the OI framework where we show how they can be easily applied to standard reconstruction problems in physical oceanography. We illustrate the relevance of NerFs for gap-filling of sparse measurements of sea surface height (SSH) via satellite altimetry and demonstrate how NerFs are scalable with comparable results to the standard OI. We find that NerFs are a practical set of methods that can be readily applied to geoscience interpolation problems and we anticipate a wider adoption in the future.

Orthonormal Convolutions for the Rotation Based Iterative Gaussianization

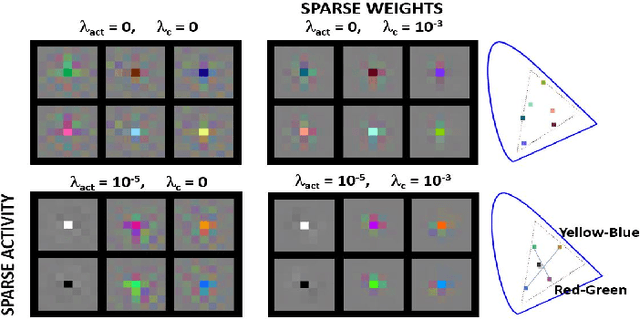
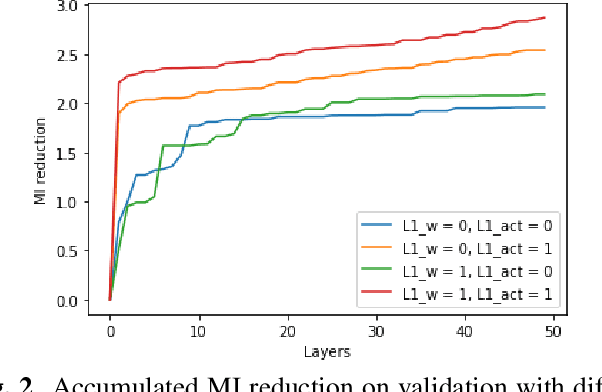
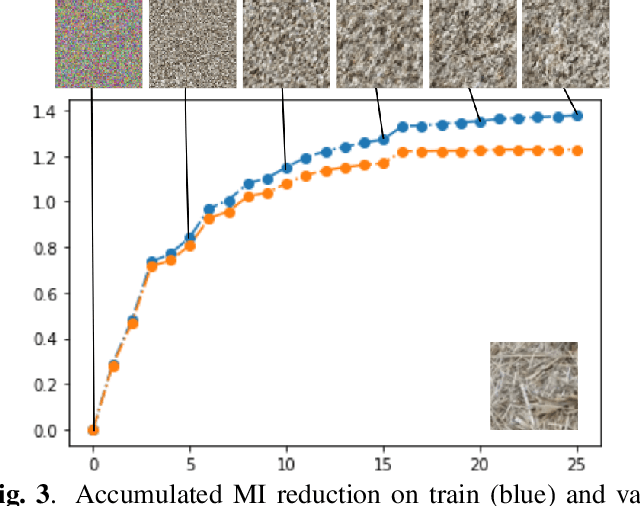
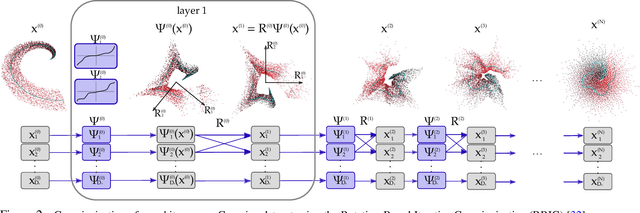
In this paper we elaborate an extension of rotation-based iterative Gaussianization, RBIG, which makes image Gaussianization possible. Although RBIG has been successfully applied to many tasks, it is limited to medium dimensionality data (on the order of a thousand dimensions). In images its application has been restricted to small image patches or isolated pixels, because rotation in RBIG is based on principal or independent component analysis and these transformations are difficult to learn and scale. Here we present the \emph{Convolutional RBIG}: an extension that alleviates this issue by imposing that the rotation in RBIG is a convolution. We propose to learn convolutional rotations (i.e. orthonormal convolutions) by optimising for the reconstruction loss between the input and an approximate inverse of the transformation using the transposed convolution operation. Additionally, we suggest different regularizers in learning these orthonormal convolutions. For example, imposing sparsity in the activations leads to a transformation that extends convolutional independent component analysis to multilayer architectures. We also highlight how statistical properties of the data, such as multivariate mutual information, can be obtained from \emph{Convolutional RBIG}. We illustrate the behavior of the transform with a simple example of texture synthesis, and analyze its properties by visualizing the stimuli that maximize the response in certain feature and layer.

The Kernelized Taylor Diagram

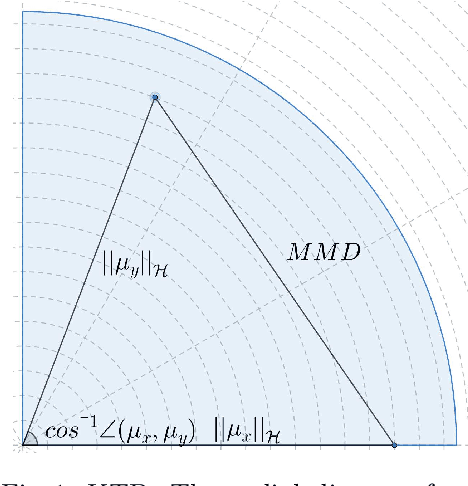
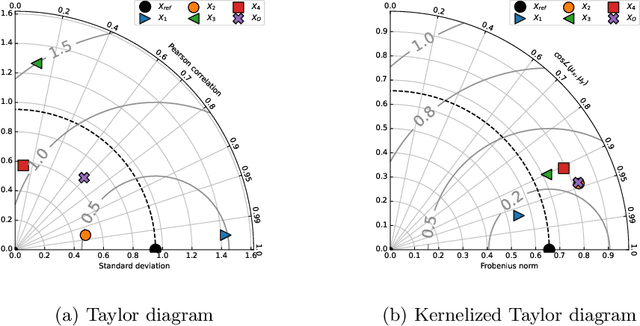
This paper presents the kernelized Taylor diagram, a graphical framework for visualizing similarities between data populations. The kernelized Taylor diagram builds on the widely used Taylor diagram, which is used to visualize similarities between populations. However, the Taylor diagram has several limitations such as not capturing non-linear relationships and sensitivity to outliers. To address such limitations, we propose the kernelized Taylor diagram. Our proposed kernelized Taylor diagram is capable of visualizing similarities between populations with minimal assumptions of the data distributions. The kernelized Taylor diagram relates the maximum mean discrepancy and the kernel mean embedding in a single diagram, a construction that, to the best of our knowledge, have not been devised prior to this work. We believe that the kernelized Taylor diagram can be a valuable tool in data visualization.

RotNet: Fast and Scalable Estimation of Stellar Rotation Periods Using Convolutional Neural Networks

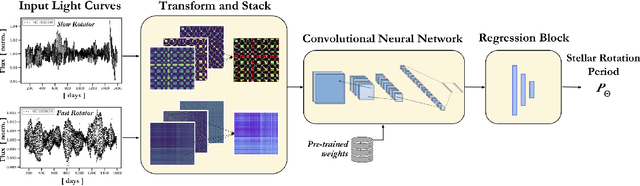
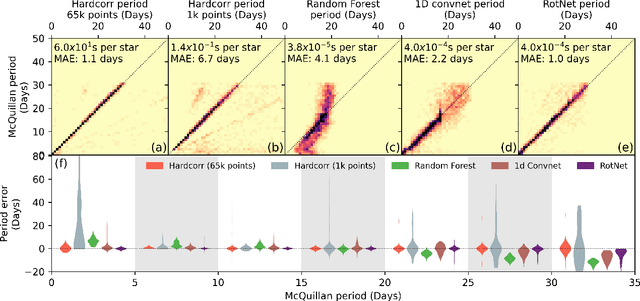
Magnetic activity in stars manifests as dark spots on their surfaces that modulate the brightness observed by telescopes. These light curves contain important information on stellar rotation. However, the accurate estimation of rotation periods is computationally expensive due to scarce ground truth information, noisy data, and large parameter spaces that lead to degenerate solutions. We harness the power of deep learning and successfully apply Convolutional Neural Networks to regress stellar rotation periods from Kepler light curves. Geometry-preserving time-series to image transformations of the light curves serve as inputs to a ResNet-18 based architecture which is trained through transfer learning. The McQuillan catalog of published rotation periods is used as ansatz to groundtruth. We benchmark the performance of our method against a random forest regressor, a 1D CNN, and the Auto-Correlation Function (ACF) - the current standard to estimate rotation periods. Despite limiting our input to fewer data points (1k), our model yields more accurate results and runs 350 times faster than ACF runs on the same number of data points and 10,000 times faster than ACF runs on 65k data points. With only minimal feature engineering our approach has impressive accuracy, motivating the application of deep learning to regress stellar parameters on an even larger scale

Information Theory in Density Destructors

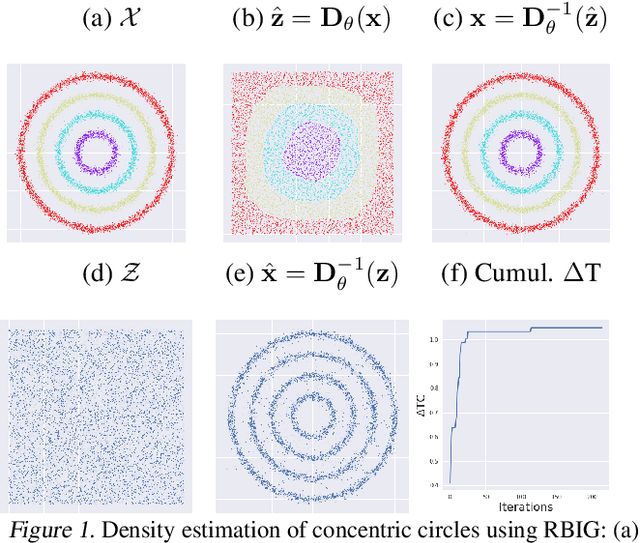
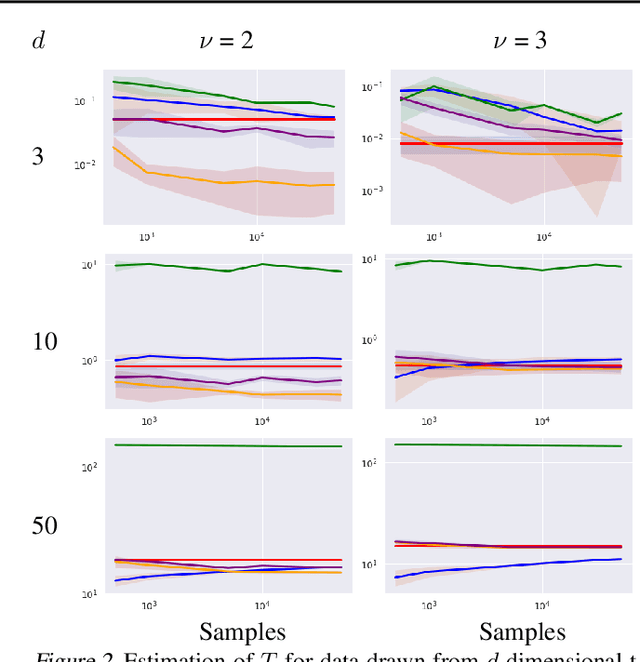
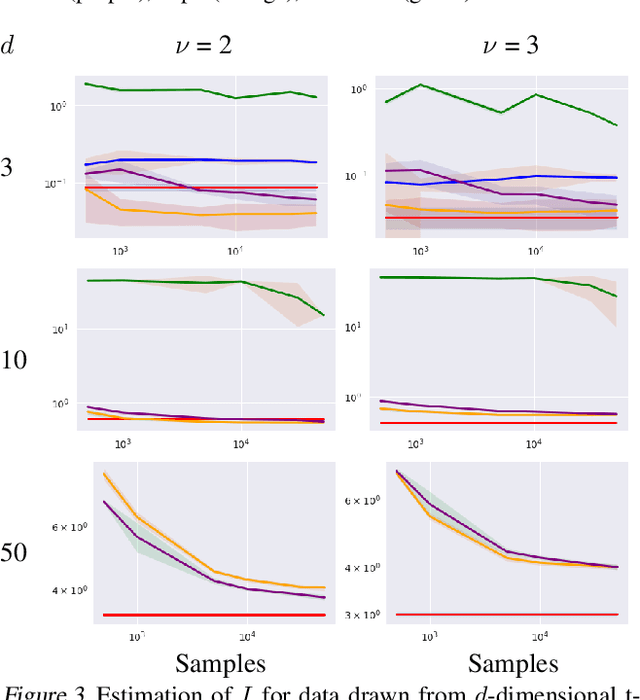
Density destructors are differentiable and invertible transforms that map multivariate PDFs of arbitrary structure (low entropy) into non-structured PDFs (maximum entropy). Multivariate Gaussianization and multivariate equalization are specific examples of this family, which break down the complexity of the original PDF through a set of elementary transforms that progressively remove the structure of the data. We demonstrate how this property of density destructive flows is connected to classical information theory, and how density destructors can be used to get more accurate estimates of information theoretic quantities. Experiments with total correlation and mutual information inmultivariate sets illustrate the ability of density destructors compared to competing methods. These results suggest that information theoretic measures may be an alternative optimization criteria when learning density destructive flows.

Gaussianizing the Earth: Multidimensional Information Measures for Earth Data Analysis

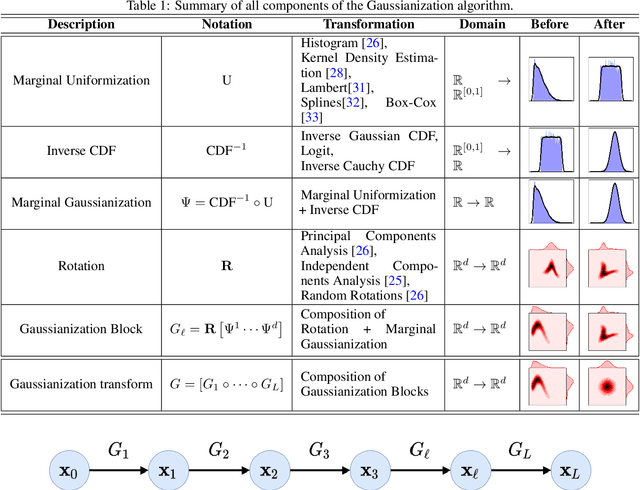
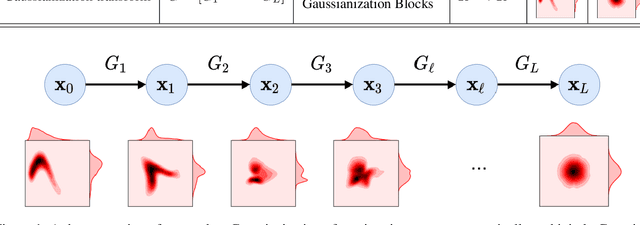
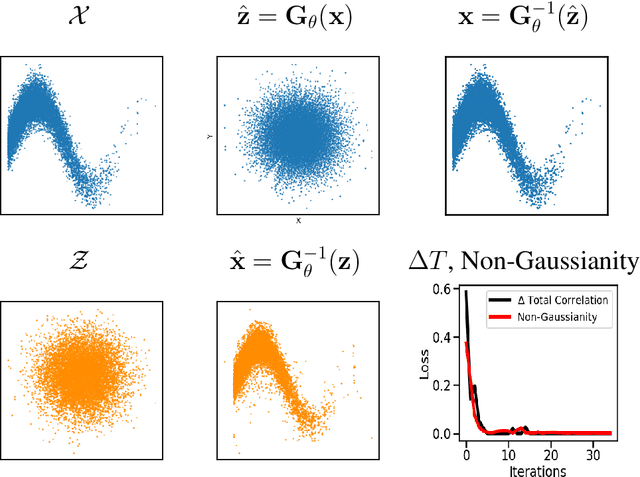
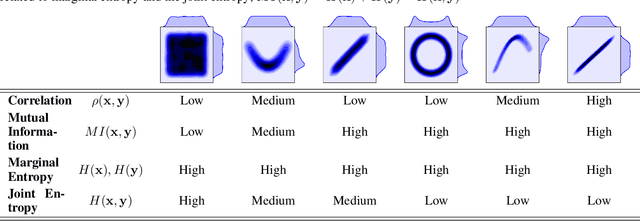
Information theory is an excellent framework for analyzing Earth system data because it allows us to characterize uncertainty and redundancy, and is universally interpretable. However, accurately estimating information content is challenging because spatio-temporal data is high-dimensional, heterogeneous and has non-linear characteristics. In this paper, we apply multivariate Gaussianization for probability density estimation which is robust to dimensionality, comes with statistical guarantees, and is easy to apply. In addition, this methodology allows us to estimate information-theoretic measures to characterize multivariate densities: information, entropy, total correlation, and mutual information. We demonstrate how information theory measures can be applied in various Earth system data analysis problems. First we show how the method can be used to jointly Gaussianize radar backscattering intensities, synthesize hyperspectral data, and quantify of information content in aerial optical images. We also quantify the information content of several variables describing the soil-vegetation status in agro-ecosystems, and investigate the temporal scales that maximize their shared information under extreme events such as droughts. Finally, we measure the relative information content of space and time dimensions in remote sensing products and model simulations involving long records of key variables such as precipitation, sensible heat and evaporation. Results confirm the validity of the method, for which we anticipate a wide use and adoption. Code and demos of the implemented algorithms and information-theory measures are provided.

Information Theory Measures via Multidimensional Gaussianization

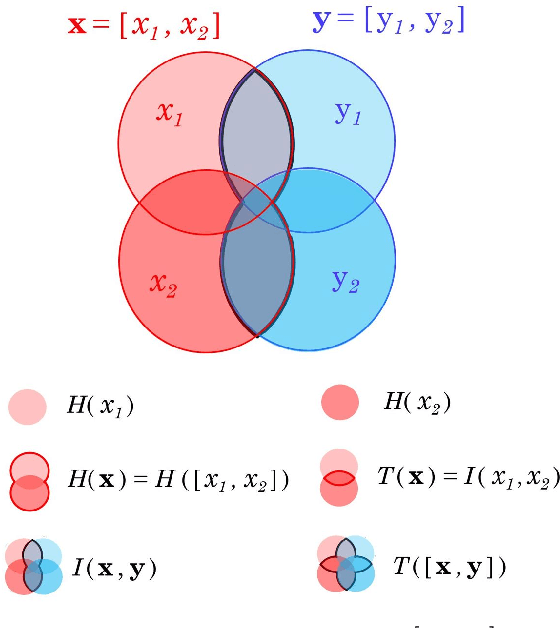
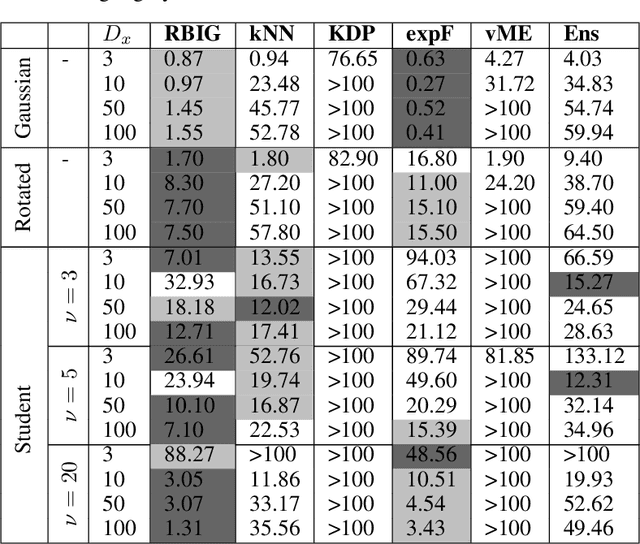
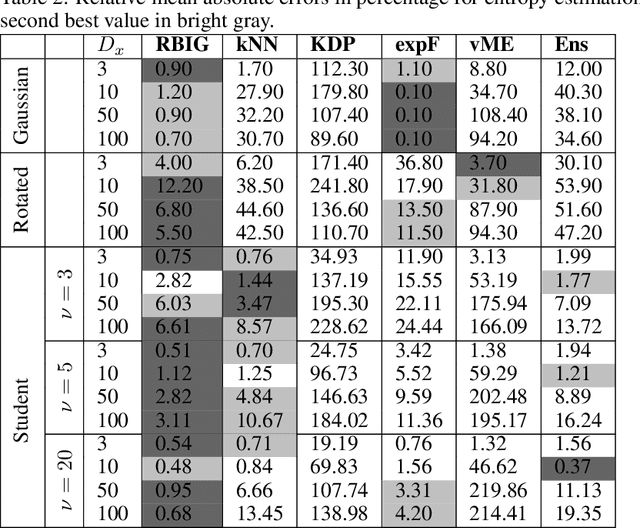
Information theory is an outstanding framework to measure uncertainty, dependence and relevance in data and systems. It has several desirable properties for real world applications: it naturally deals with multivariate data, it can handle heterogeneous data types, and the measures can be interpreted in physical units. However, it has not been adopted by a wider audience because obtaining information from multidimensional data is a challenging problem due to the curse of dimensionality. Here we propose an indirect way of computing information based on a multivariate Gaussianization transform. Our proposal mitigates the difficulty of multivariate density estimation by reducing it to a composition of tractable (marginal) operations and simple linear transformations, which can be interpreted as a particular deep neural network. We introduce specific Gaussianization-based methodologies to estimate total correlation, entropy, mutual information and Kullback-Leibler divergence. We compare them to recent estimators showing the accuracy on synthetic data generated from different multivariate distributions. We made the tools and datasets publicly available to provide a test-bed to analyze future methodologies. Results show that our proposal is superior to previous estimators particularly in high-dimensional scenarios; and that it leads to interesting insights in neuroscience, geoscience, computer vision, and machine learning.

Kernel Methods and their derivatives: Concept and perspectives for the Earth system sciences

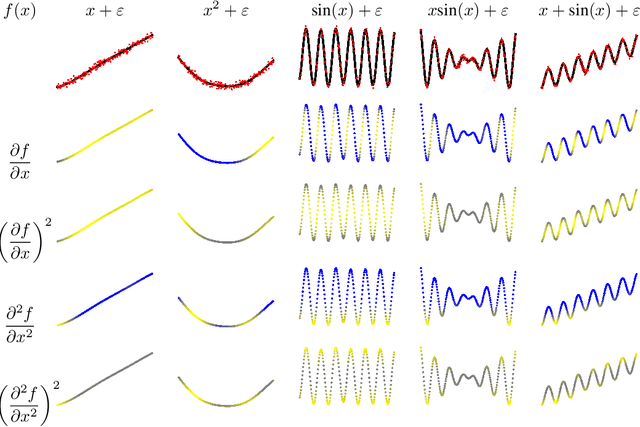
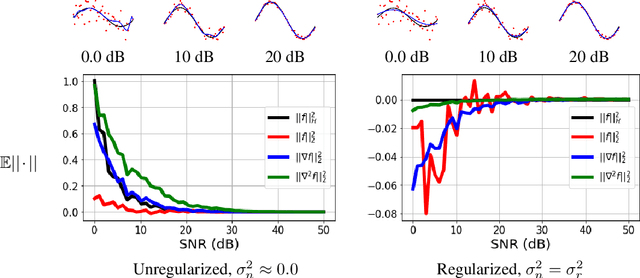
Kernel methods are powerful machine learning techniques which implement generic non-linear functions to solve complex tasks in a simple way. They Have a solid mathematical background and exhibit excellent performance in practice. However, kernel machines are still considered black-box models as the feature mapping is not directly accessible and difficult to interpret.The aim of this work is to show that it is indeed possible to interpret the functions learned by various kernel methods is intuitive despite their complexity. Specifically, we show that derivatives of these functions have a simple mathematical formulation, are easy to compute, and can be applied to many different problems. We note that model function derivatives in kernel machines is proportional to the kernel function derivative. We provide the explicit analytic form of the first and second derivatives of the most common kernel functions with regard to the inputs as well as generic formulas to compute higher order derivatives. We use them to analyze the most used supervised and unsupervised kernel learning methods: Gaussian Processes for regression, Support Vector Machines for classification, Kernel Entropy Component Analysis for density estimation, and the Hilbert-Schmidt Independence Criterion for estimating the dependency between random variables. For all cases we expressed the derivative of the learned function as a linear combination of the kernel function derivative. Moreover we provide intuitive explanations through illustrative toy examples and show how to improve the interpretation of real applications in the context of spatiotemporal Earth system data cubes. This work reflects on the observation that function derivatives may play a crucial role in kernel methods analysis and understanding.