Information Theory Measures via Multidimensional Gaussianization
Paper and Code
Oct 08, 2020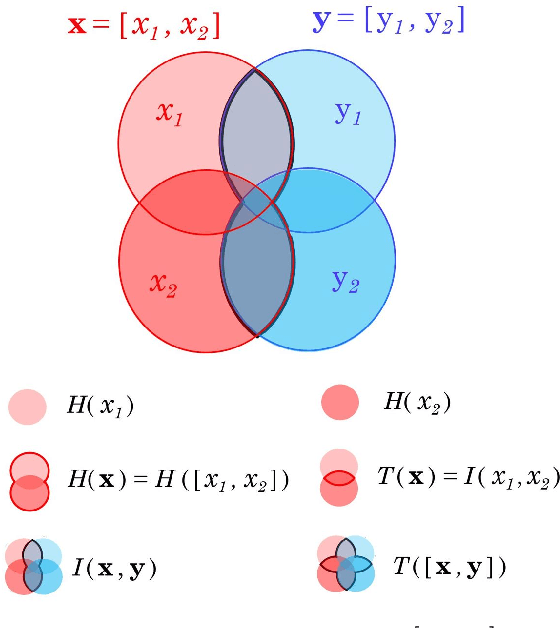
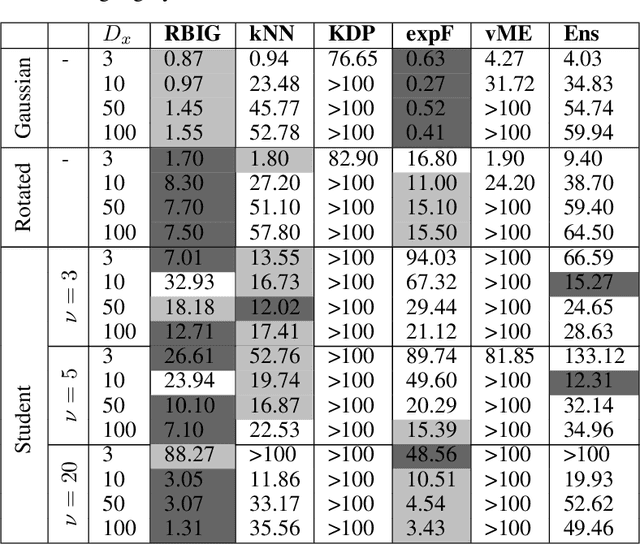
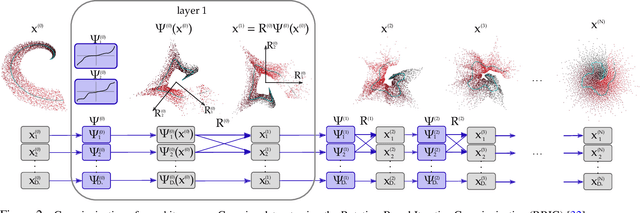
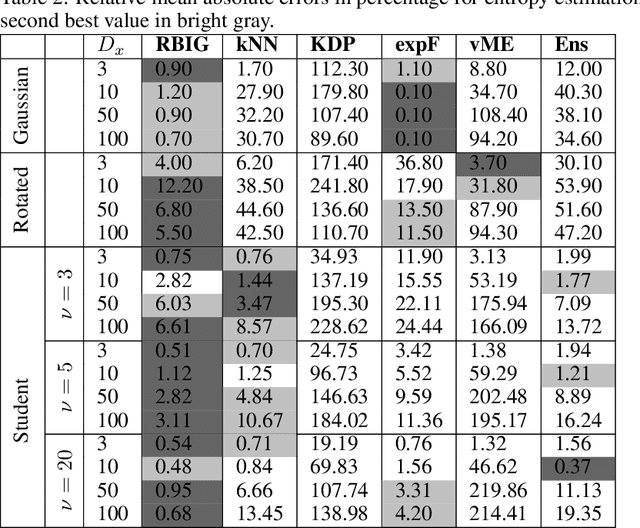
Information theory is an outstanding framework to measure uncertainty, dependence and relevance in data and systems. It has several desirable properties for real world applications: it naturally deals with multivariate data, it can handle heterogeneous data types, and the measures can be interpreted in physical units. However, it has not been adopted by a wider audience because obtaining information from multidimensional data is a challenging problem due to the curse of dimensionality. Here we propose an indirect way of computing information based on a multivariate Gaussianization transform. Our proposal mitigates the difficulty of multivariate density estimation by reducing it to a composition of tractable (marginal) operations and simple linear transformations, which can be interpreted as a particular deep neural network. We introduce specific Gaussianization-based methodologies to estimate total correlation, entropy, mutual information and Kullback-Leibler divergence. We compare them to recent estimators showing the accuracy on synthetic data generated from different multivariate distributions. We made the tools and datasets publicly available to provide a test-bed to analyze future methodologies. Results show that our proposal is superior to previous estimators particularly in high-dimensional scenarios; and that it leads to interesting insights in neuroscience, geoscience, computer vision, and machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge