Contrast Sensitivity Function of Multimodal Vision-Language Models

Assessing the alignment of multimodal vision-language models~(VLMs) with human perception is essential to understand how they perceive low-level visual features. A key characteristic of human vision is the contrast sensitivity function (CSF), which describes sensitivity to spatial frequency at low-contrasts. Here, we introduce a novel behavioral psychophysics-inspired method to estimate the CSF of chat-based VLMs by directly prompting them to judge pattern visibility at different contrasts for each frequency. This methodology is closer to the real experiments in psychophysics than the previously reported. Using band-pass filtered noise images and a diverse set of prompts, we assess model responses across multiple architectures. We find that while some models approximate human-like CSF shape or magnitude, none fully replicate both. Notably, prompt phrasing has a large effect on the responses, raising concerns about prompt stability. Our results provide a new framework for probing visual sensitivity in multimodal models and reveal key gaps between their visual representations and human perception.

The Art of Deception: Color Visual Illusions and Diffusion Models

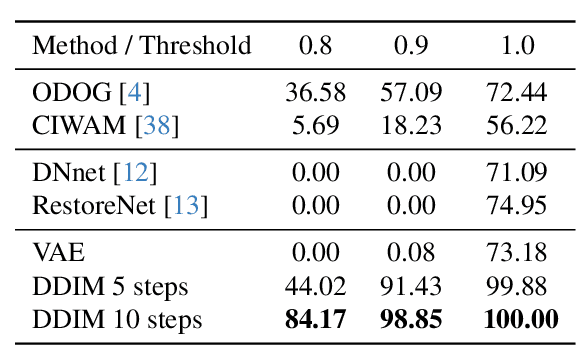
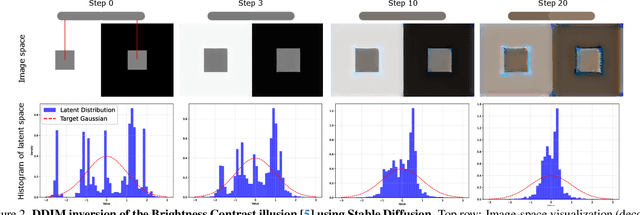
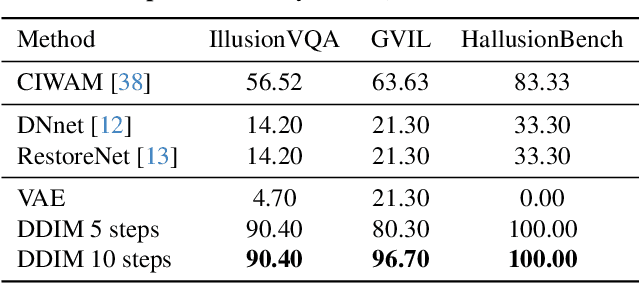
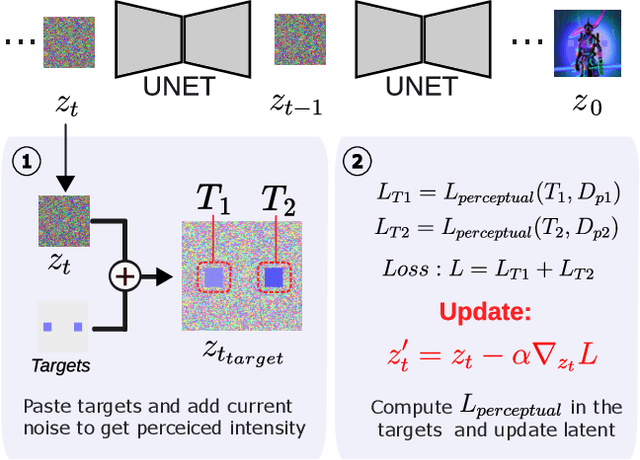
Visual illusions in humans arise when interpreting out-of-distribution stimuli: if the observer is adapted to certain statistics, perception of outliers deviates from reality. Recent studies have shown that artificial neural networks (ANNs) can also be deceived by visual illusions. This revelation raises profound questions about the nature of visual information. Why are two independent systems, both human brains and ANNs, susceptible to the same illusions? Should any ANN be capable of perceiving visual illusions? Are these perceptions a feature or a flaw? In this work, we study how visual illusions are encoded in diffusion models. Remarkably, we show that they present human-like brightness/color shifts in their latent space. We use this fact to demonstrate that diffusion models can predict visual illusions. Furthermore, we also show how to generate new unseen visual illusions in realistic images using text-to-image diffusion models. We validate this ability through psychophysical experiments that show how our model-generated illusions also fool humans.

The Effect of Perceptual Metrics on Music Representation Learning for Genre Classification

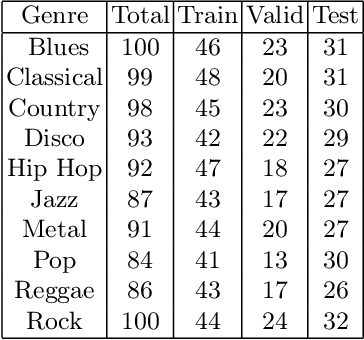
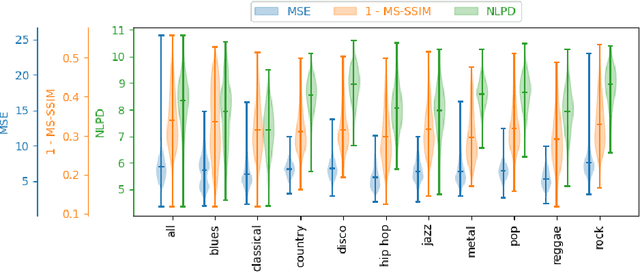
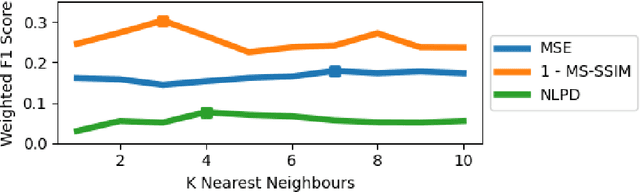
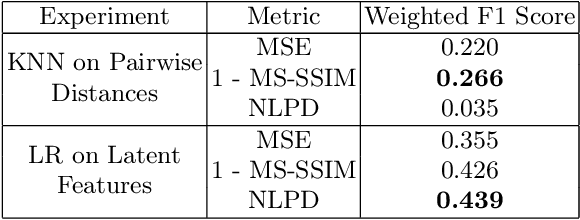
The subjective quality of natural signals can be approximated with objective perceptual metrics. Designed to approximate the perceptual behaviour of human observers, perceptual metrics often reflect structures found in natural signals and neurological pathways. Models trained with perceptual metrics as loss functions can capture perceptually meaningful features from the structures held within these metrics. We demonstrate that using features extracted from autoencoders trained with perceptual losses can improve performance on music understanding tasks, i.e. genre classification, over using these metrics directly as distances when learning a classifier. This result suggests improved generalisation to novel signals when using perceptual metrics as loss functions for representation learning.

Data is Overrated: Perceptual Metrics Can Lead Learning in the Absence of Training Data

Perceptual metrics are traditionally used to evaluate the quality of natural signals, such as images and audio. They are designed to mimic the perceptual behaviour of human observers and usually reflect structures found in natural signals. This motivates their use as loss functions for training generative models such that models will learn to capture the structure held in the metric. We take this idea to the extreme in the audio domain by training a compressive autoencoder to reconstruct uniform noise, in lieu of natural data. We show that training with perceptual losses improves the reconstruction of spectrograms and re-synthesized audio at test time over models trained with a standard Euclidean loss. This demonstrates better generalisation to unseen natural signals when using perceptual metrics.

What You Hear Is What You See: Audio Quality Metrics From Image Quality Metrics

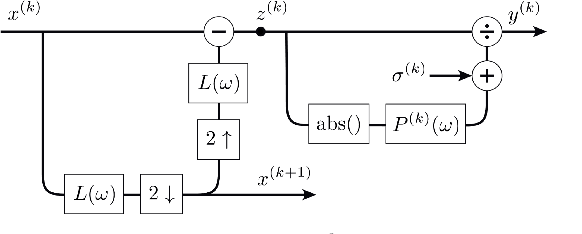
In this study, we investigate the feasibility of utilizing state-of-the-art image perceptual metrics for evaluating audio signals by representing them as spectrograms. The encouraging outcome of the proposed approach is based on the similarity between the neural mechanisms in the auditory and visual pathways. Furthermore, we customise one of the metrics which has a psychoacoustically plausible architecture to account for the peculiarities of sound signals. We evaluate the effectiveness of our proposed metric and several baseline metrics using a music dataset, with promising results in terms of the correlation between the metrics and the perceived quality of audio as rated by human evaluators.

Paraphrasing Magritte's Observation

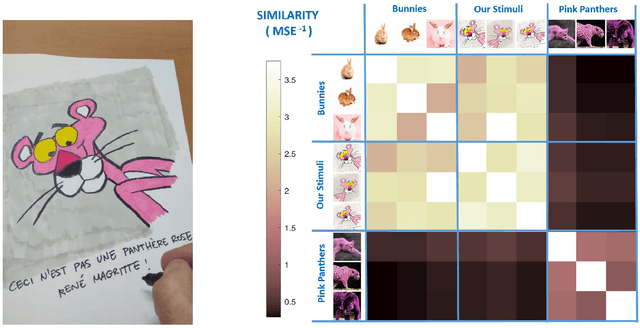
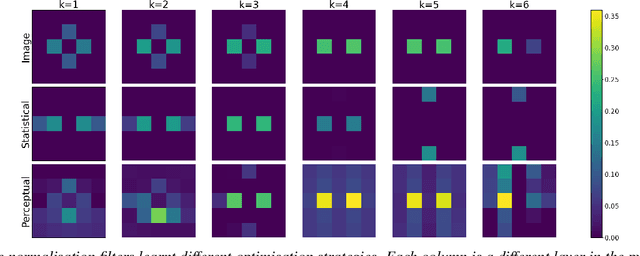
Contrast Sensitivity of the human visual system can be explained from certain low-level vision tasks (like retinal noise and optical blur removal), but not from others (like chromatic adaptation or pure reconstruction after simple bottlenecks). This conclusion still holds even under substantial change in stimulus statistics, as for instance considering cartoon-like images as opposed to natural images (Li et al. Journal of Vision, 2022, Preprint arXiv:2103.00481). In this note we present a method to generate original cartoon-like images compatible with the statistical training used in (Li et al., 2022). Following the classical observation in (Magritte, 1929), the stimuli generated by the proposed method certainly are not what they represent: Ceci n'est pas une pipe. The clear distinction between representation (the stimuli generated by the proposed method) and reality (the actual object) avoids eventual problems for the use of the generated stimuli in academic, non-profit, publications.

Information Theory Measures via Multidimensional Gaussianization

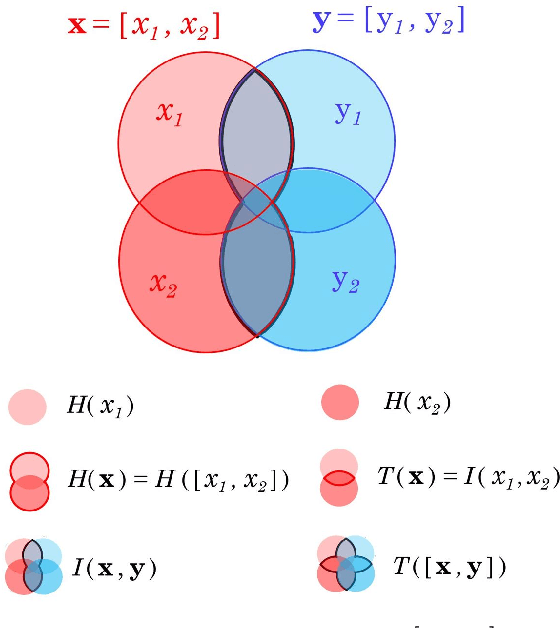
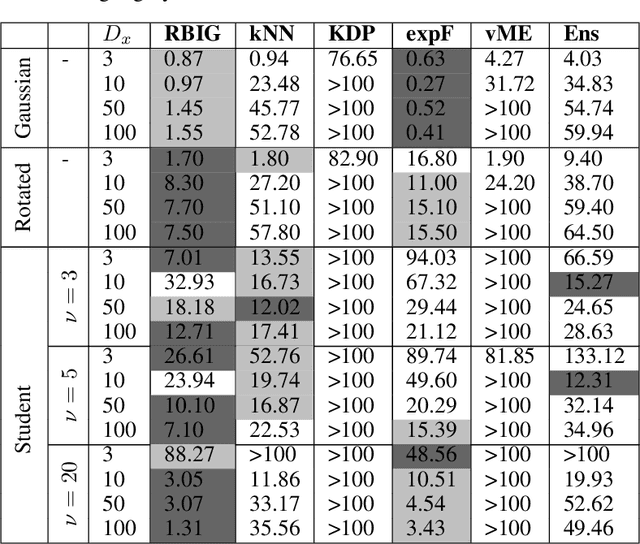
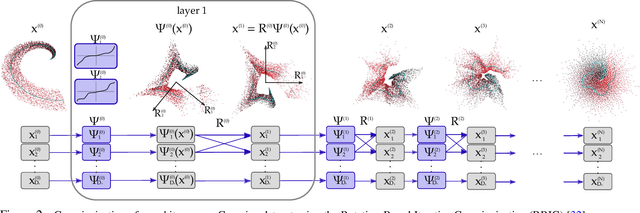
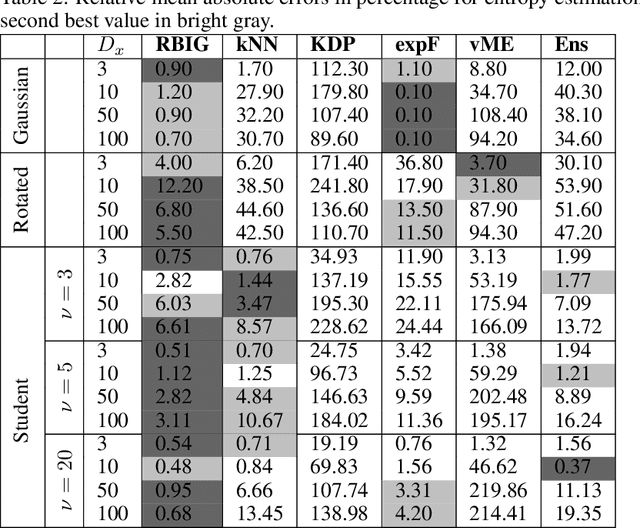
Information theory is an outstanding framework to measure uncertainty, dependence and relevance in data and systems. It has several desirable properties for real world applications: it naturally deals with multivariate data, it can handle heterogeneous data types, and the measures can be interpreted in physical units. However, it has not been adopted by a wider audience because obtaining information from multidimensional data is a challenging problem due to the curse of dimensionality. Here we propose an indirect way of computing information based on a multivariate Gaussianization transform. Our proposal mitigates the difficulty of multivariate density estimation by reducing it to a composition of tractable (marginal) operations and simple linear transformations, which can be interpreted as a particular deep neural network. We introduce specific Gaussianization-based methodologies to estimate total correlation, entropy, mutual information and Kullback-Leibler divergence. We compare them to recent estimators showing the accuracy on synthetic data generated from different multivariate distributions. We made the tools and datasets publicly available to provide a test-bed to analyze future methodologies. Results show that our proposal is superior to previous estimators particularly in high-dimensional scenarios; and that it leads to interesting insights in neuroscience, geoscience, computer vision, and machine learning.

Sequential Principal Curves Analysis

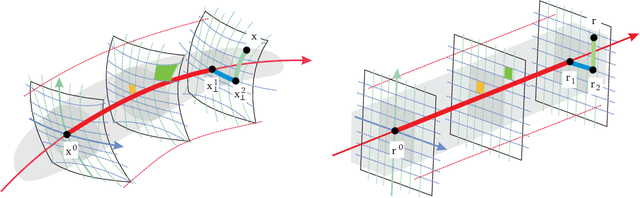
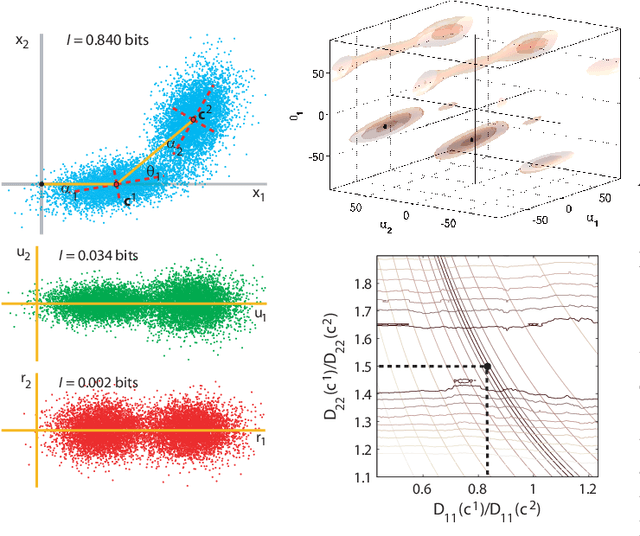
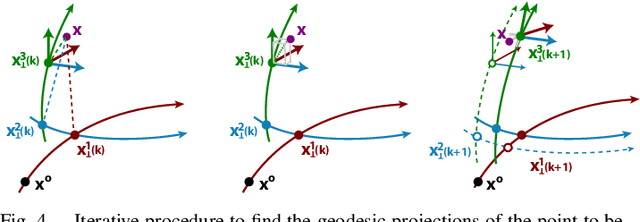
This work includes all the technical details of the Sequential Principal Curves Analysis (SPCA) in a single document. SPCA is an unsupervised nonlinear and invertible feature extraction technique. The identified curvilinear features can be interpreted as a set of nonlinear sensors: the response of each sensor is the projection onto the corresponding feature. Moreover, it can be easily tuned for different optimization criteria; e.g. infomax, error minimization, decorrelation; by choosing the right way to measure distances along each curvilinear feature. Even though proposed in [Laparra et al. Neural Comp. 12] and shown to work in multiple modalities in [Laparra and Malo Frontiers Hum. Neuro. 15], the SPCA framework has its original roots in the nonlinear ICA algorithm in [Malo and Gutierrez Network 06]. Later on, the SPCA philosophy for nonlinear generalization of PCA originated substantially faster alternatives at the cost of introducing different constraints in the model. Namely, the Principal Polynomial Analysis (PPA) [Laparra et al. IJNS 14], and the Dimensionality Reduction via Regression (DRR) [Laparra et al. IEEE TGRS 15]. This report illustrates the reasons why we developed such family and is the appropriate technical companion for the missing details in [Laparra et al., NeCo 12, Laparra and Malo, Front.Hum.Neuro. 15]. See also the data, code and examples in the dedicated sites http://isp.uv.es/spca.html and http://isp.uv.es/after effects.html

Dimensionality Reduction via Regression in Hyperspectral Imagery

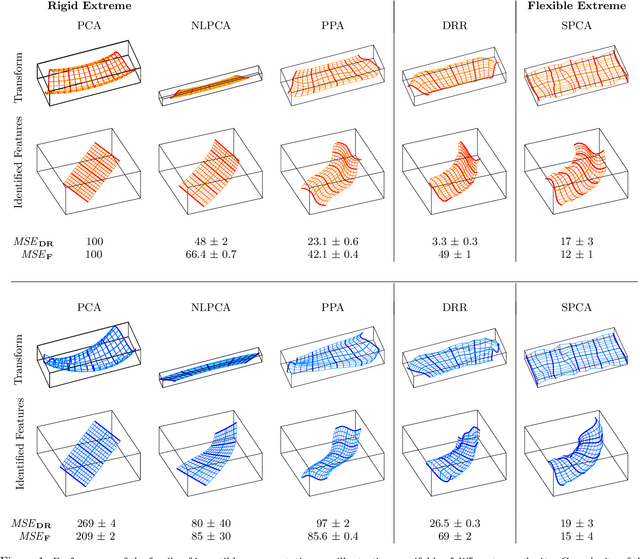
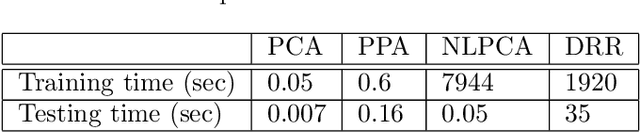
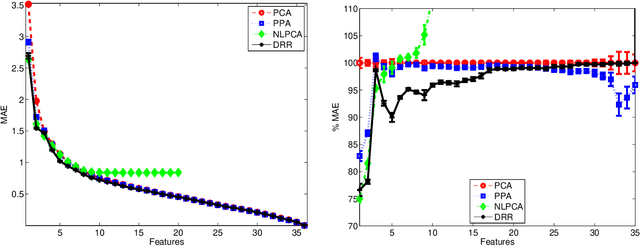
This paper introduces a new unsupervised method for dimensionality reduction via regression (DRR). The algorithm belongs to the family of invertible transforms that generalize Principal Component Analysis (PCA) by using curvilinear instead of linear features. DRR identifies the nonlinear features through multivariate regression to ensure the reduction in redundancy between he PCA coefficients, the reduction of the variance of the scores, and the reduction in the reconstruction error. More importantly, unlike other nonlinear dimensionality reduction methods, the invertibility, volume-preservation, and straightforward out-of-sample extension, makes DRR interpretable and easy to apply. The properties of DRR enable learning a more broader class of data manifolds than the recently proposed Non-linear Principal Components Analysis (NLPCA) and Principal Polynomial Analysis (PPA). We illustrate the performance of the representation in reducing the dimensionality of remote sensing data. In particular, we tackle two common problems: processing very high dimensional spectral information such as in hyperspectral image sounding data, and dealing with spatial-spectral image patches of multispectral images. Both settings pose collinearity and ill-determination problems. Evaluation of the expressive power of the features is assessed in terms of truncation error, estimating atmospheric variables, and surface land cover classification error. Results show that DRR outperforms linear PCA and recently proposed invertible extensions based on neural networks (NLPCA) and univariate regressions (PPA).