Orthonormal Convolutions for the Rotation Based Iterative Gaussianization
Paper and Code
Jun 08, 2022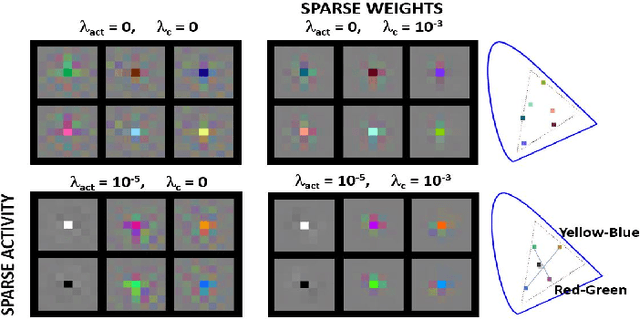
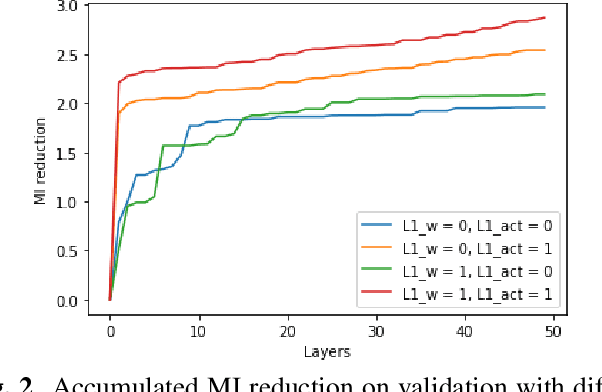
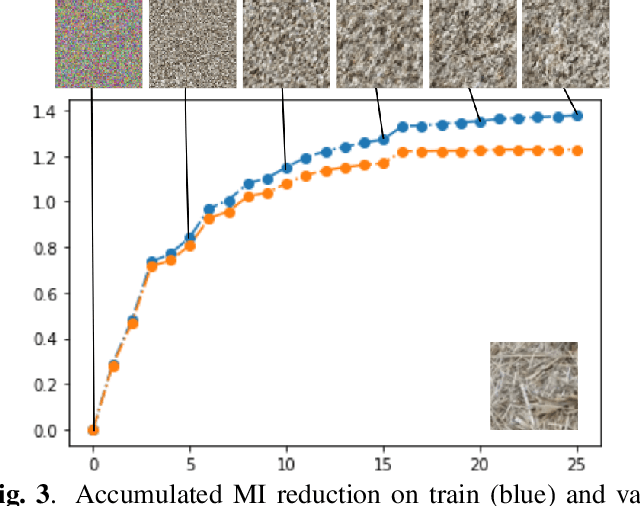

In this paper we elaborate an extension of rotation-based iterative Gaussianization, RBIG, which makes image Gaussianization possible. Although RBIG has been successfully applied to many tasks, it is limited to medium dimensionality data (on the order of a thousand dimensions). In images its application has been restricted to small image patches or isolated pixels, because rotation in RBIG is based on principal or independent component analysis and these transformations are difficult to learn and scale. Here we present the \emph{Convolutional RBIG}: an extension that alleviates this issue by imposing that the rotation in RBIG is a convolution. We propose to learn convolutional rotations (i.e. orthonormal convolutions) by optimising for the reconstruction loss between the input and an approximate inverse of the transformation using the transposed convolution operation. Additionally, we suggest different regularizers in learning these orthonormal convolutions. For example, imposing sparsity in the activations leads to a transformation that extends convolutional independent component analysis to multilayer architectures. We also highlight how statistical properties of the data, such as multivariate mutual information, can be obtained from \emph{Convolutional RBIG}. We illustrate the behavior of the transform with a simple example of texture synthesis, and analyze its properties by visualizing the stimuli that maximize the response in certain feature and layer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge