SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

Online machine-learning forecast uncertainty estimation for sequential data assimilation

Quantifying forecast uncertainty is a key aspect of state-of-the-art numerical weather prediction and data assimilation systems. Ensemble-based data assimilation systems incorporate state-dependent uncertainty quantification based on multiple model integrations. However, this approach is demanding in terms of computations and development. In this work a machine learning method is presented based on convolutional neural networks that estimates the state-dependent forecast uncertainty represented by the forecast error covariance matrix using a single dynamical model integration. This is achieved by the use of a loss function that takes into account the fact that the forecast errors are heterodastic. The performance of this approach is examined within a hybrid data assimilation method that combines a Kalman-like analysis update and the machine learning based estimation of a state-dependent forecast error covariance matrix. Observing system simulation experiments are conducted using the Lorenz'96 model as a proof-of-concept. The promising results show that the machine learning method is able to predict precise values of the forecast covariance matrix in relatively high-dimensional states. Moreover, the hybrid data assimilation method shows similar performance to the ensemble Kalman filter outperforming it when the ensembles are relatively small.

Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review

Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.

Reduction of rain-induced errors for wind speed estimation on SAR observations using convolutional neural networks

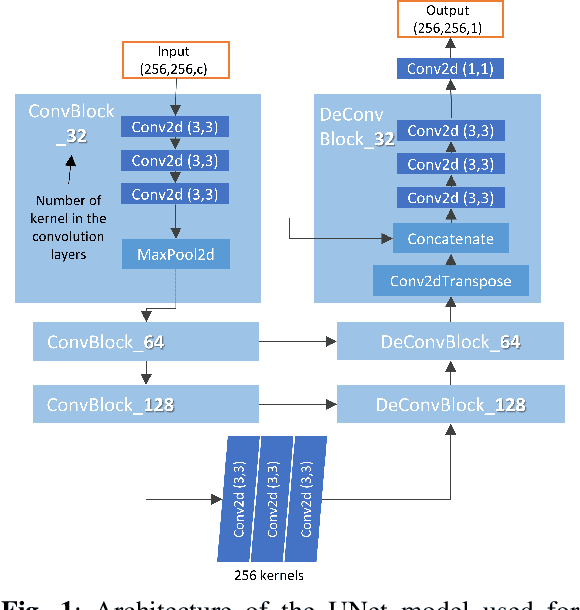
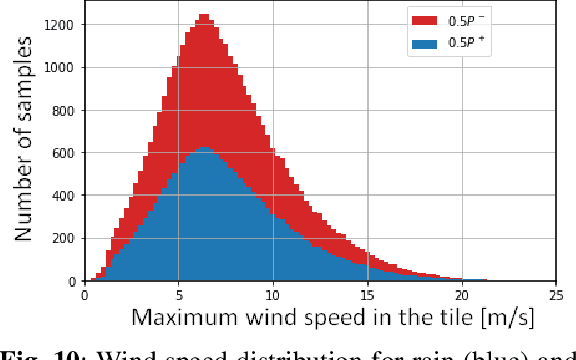
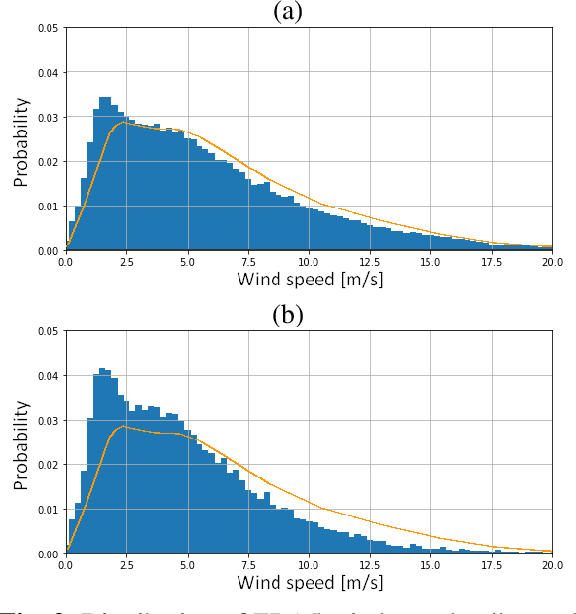
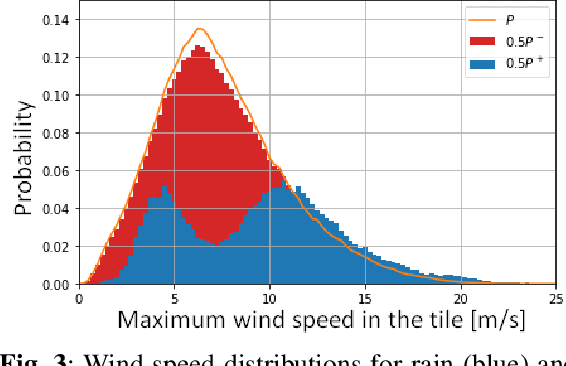
Synthetic Aperture Radar is known to be able to provide high-resolution estimates of surface wind speed. These estimates usually rely on a Geophysical Model Function (GMF) that has difficulties accounting for non-wind processes such as rain events. Convolutional neural network, on the other hand, have the capacity to use contextual information and have demonstrated their ability to delimit rainfall areas. By carefully building a large dataset of SAR observations from the Copernicus Sentinel-1 mission, collocated with both GMF and atmospheric model wind speeds as well as rainfall estimates, we were able to train a wind speed estimator with reduced errors under rain. Collocations with in-situ wind speed measurements from buoys show a root mean square error that is reduced by 27% (resp. 45%) under rainfall estimated at more than 1 mm/h (resp. 3 mm/h). These results demonstrate the capacity of deep learning models to correct rain-related errors in SAR products.

Rain Rate Estimation with SAR using NEXRAD measurements with Convolutional Neural Networks

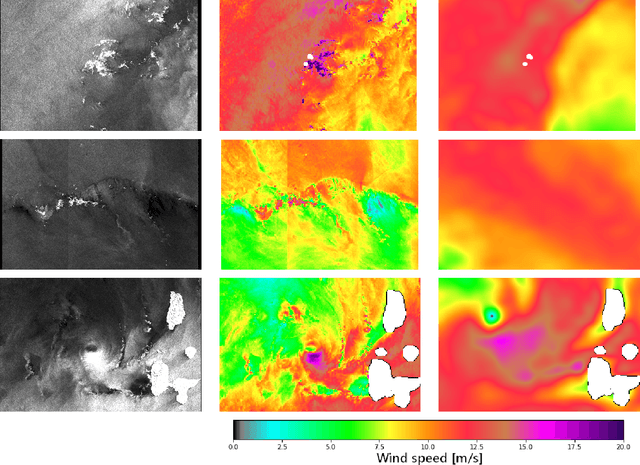
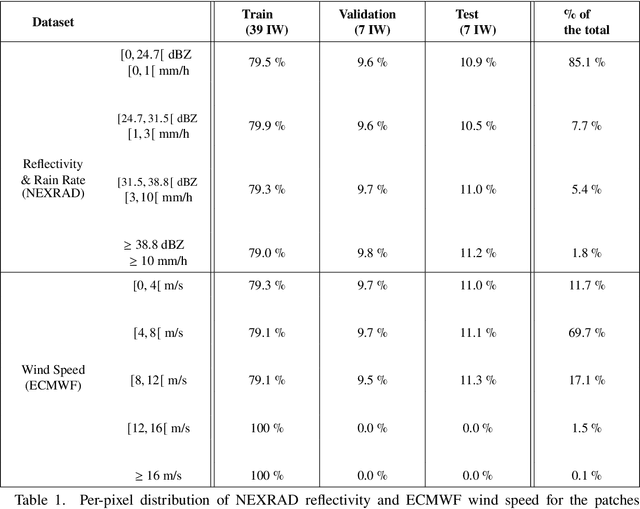
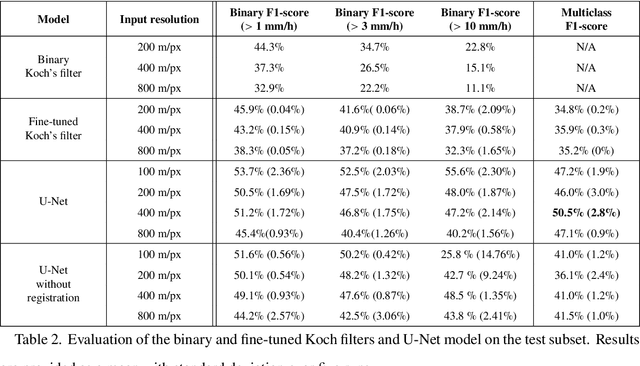
Remote sensing of rainfall events is critical for both operational and scientific needs, including for example weather forecasting, extreme flood mitigation, water cycle monitoring, etc. Ground-based weather radars, such as NOAA's Next-Generation Radar (NEXRAD), provide reflectivity and precipitation measurements of rainfall events. However, the observation range of such radars is limited to a few hundred kilometers, prompting the exploration of other remote sensing methods, paricularly over the open ocean, that represents large areas not covered by land-based radars. For a number of decades, C-band SAR imagery such a such as Sentinel-1 imagery has been known to exhibit rainfall signatures over the sea surface. However, the development of SAR-derived rainfall products remains a challenge. Here we propose a deep learning approach to extract rainfall information from SAR imagery. We demonstrate that a convolutional neural network, such as U-Net, trained on a colocated and preprocessed Sentinel-1/NEXRAD dataset clearly outperforms state-of-the-art filtering schemes. Our results indicate high performance in segmenting precipitation regimes, delineated by thresholds at 1, 3, and 10 mm/h. Compared to current methods that rely on Koch filters to draw binary rainfall maps, these multi-threshold learning-based models can provide rainfall estimation for higher wind speeds and thus may be of great interest for data assimilation weather forecasting or for improving the qualification of SAR-derived wind field data.

Two-dimensional structure functions to characterize convective rolls in the marine atmospheric boundary layer from Sentinel-1 SAR images

We study the shape of convective rolls in the Marine Atmospheric Boundary Layer from Synthetic Aperture Radar images of the ocean. We propose a multiscale analysis with structure functions which allow an easy generalization to analyse high-order statistics and so to finely describe the shape of the rolls. The two main results are : 1) second order structure function characterizes the size and direction of rolls just like correlation or power spectrum do, 2) high order statistics can be studied with skewness and Flatness which characterize the asymmetry and intermittency of rolls respectively. From the best of our knowledge, this is the first time that the asymmetry and intermittency of rolls is shown from radar images of the ocean surface.

Evaluation of Machine Learning Techniques for Forecast Uncertainty Quantification

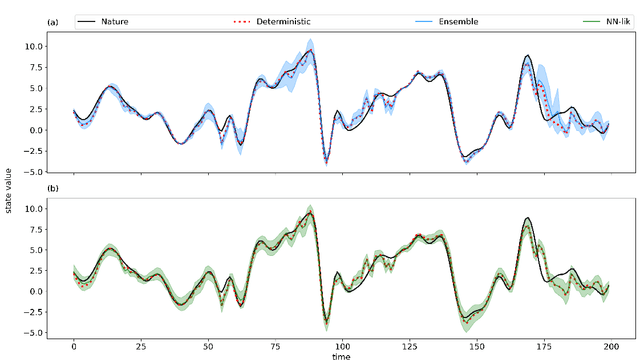
Producing an accurate weather forecast and a reliable quantification of its uncertainty is an open scientific challenge. Ensemble forecasting is, so far, the most successful approach to produce relevant forecasts along with an estimation of their uncertainty. The main limitations of ensemble forecasting are the high computational cost and the difficulty to capture and quantify different sources of uncertainty, particularly those associated with model errors. In this work proof-of-concept model experiments are conducted to examine the performance of ANNs trained to predict a corrected state of the system and the state uncertainty using only a single deterministic forecast as input. We compare different training strategies: one based on a direct training using the mean and spread of an ensemble forecast as target, the other ones rely on an indirect training strategy using a deterministic forecast as target in which the uncertainty is implicitly learned from the data. For the last approach two alternative loss functions are proposed and evaluated, one based on the data observation likelihood and the other one based on a local estimation of the error. The performance of the networks is examined at different lead times and in scenarios with and without model errors. Experiments using the Lorenz'96 model show that the ANNs are able to emulate some of the properties of ensemble forecasts like the filtering of the most unpredictable modes and a state-dependent quantification of the forecast uncertainty. Moreover, ANNs provide a reliable estimation of the forecast uncertainty in the presence of model error.

Probability distributions for analog-to-target distances

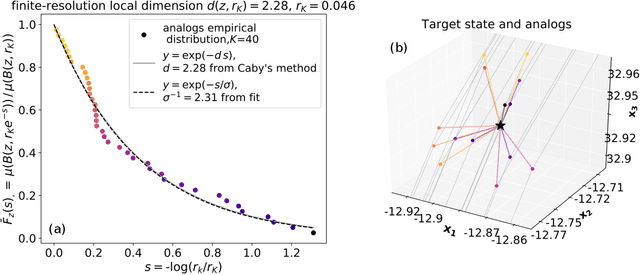
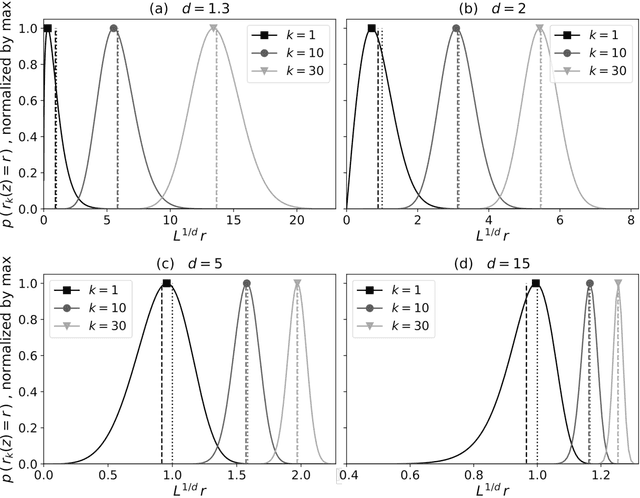
Some properties of chaotic dynamical systems can be probed through features of recurrences, also called analogs. In practice, analogs are nearest neighbours of the state of a system, taken from a large database called the catalog. Analogs have been used in many atmospheric applications including forecasts, downscaling, predictability estimation, and attribution of extreme events. The distances of the analogs to the target state condition the performances of analog applications. These distances can be viewed as random variables, and their probability distributions can be related to the catalog size and properties of the system at stake. A few studies have focused on the first moments of return time statistics for the best analog, fixing an objective of maximum distance from this analog to the target state. However, for practical use and to reduce estimation variance, applications usually require not just one, but many analogs. In this paper, we evaluate from a theoretical standpoint and with numerical experiments the probability distributions of the $K$-best analog-to-target distances. We show that dimensionality plays a role on the size of the catalog needed to find good analogs, and also on the relative means and variances of the $K$-best analogs. Our results are based on recently developed tools from dynamical systems theory. These findings are illustrated with numerical simulations of a well-known chaotic dynamical system and on 10m-wind reanalysis data in north-west France. A practical application of our derivations for the purpose of objective-based dimension reduction is shown using the same reanalysis data.

Coupling Oceanic Observation Systems to Study Mesoscale Ocean Dynamics

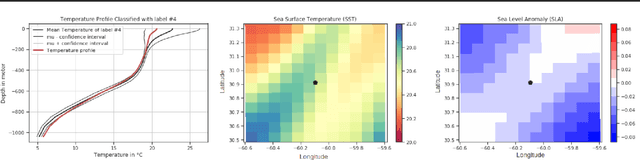
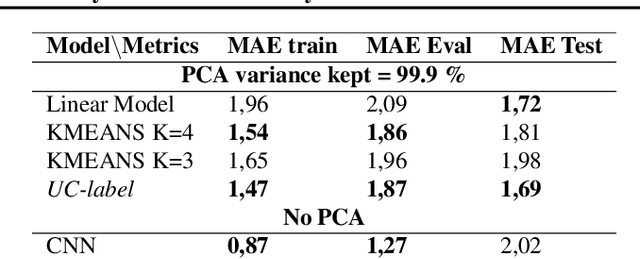
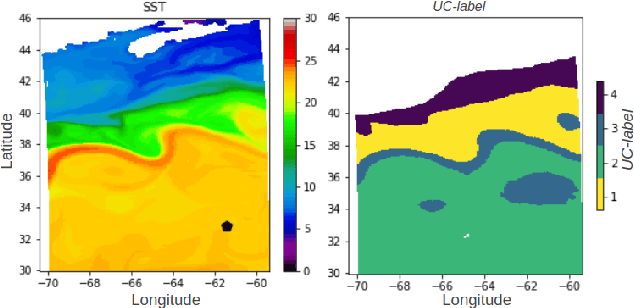
Understanding local currents in the North Atlantic region of the ocean is a key part of modelling heat transfer and global climate patterns. Satellites provide a surface signature of the temperature of the ocean with a high horizontal resolution while in situ autonomous probes supply high vertical resolution, but horizontally sparse, knowledge of the ocean interior thermal structure. The objective of this paper is to develop a methodology to combine these complementary ocean observing systems measurements to obtain a three-dimensional time series of ocean temperatures with high horizontal and vertical resolution. Within an observation-driven framework, we investigate the extent to which mesoscale ocean dynamics in the North Atlantic region may be decomposed into a mixture of dynamical modes, characterized by different local regressions between Sea Surface Temperature (SST), Sea Level Anomalies (SLA) and Vertical Temperature fields. Ultimately we propose a Latent-class regression method to improve prediction of vertical ocean temperature.

EddyNet: A Deep Neural Network For Pixel-Wise Classification of Oceanic Eddies

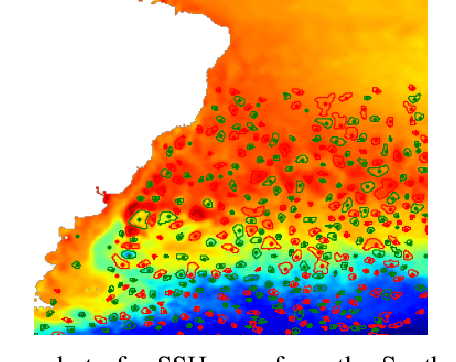
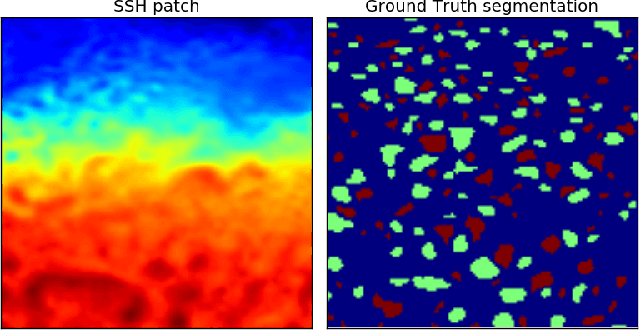
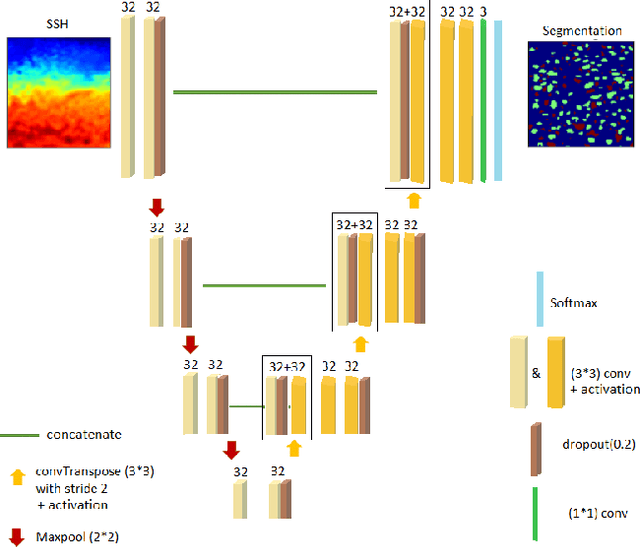
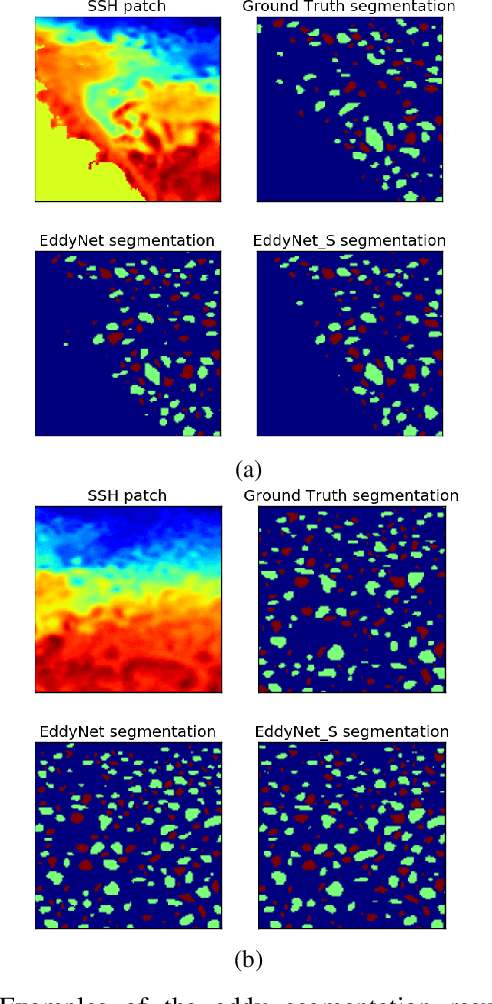
This work presents EddyNet, a deep learning based architecture for automated eddy detection and classification from Sea Surface Height (SSH) maps provided by the Copernicus Marine and Environment Monitoring Service (CMEMS). EddyNet is a U-Net like network that consists of a convolutional encoder-decoder followed by a pixel-wise classification layer. The output is a map with the same size of the input where pixels have the following labels \{'0': Non eddy, '1': anticyclonic eddy, '2': cyclonic eddy\}. We investigate the use of SELU activation function instead of the classical ReLU+BN and we use an overlap based loss function instead of the cross entropy loss. Keras Python code, the training datasets and EddyNet weights files are open-source and freely available on https://github.com/redouanelg/EddyNet.