AI for Extreme Event Modeling and Understanding: Methodologies and Challenges

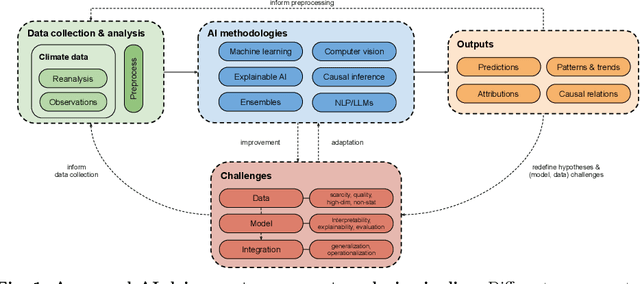
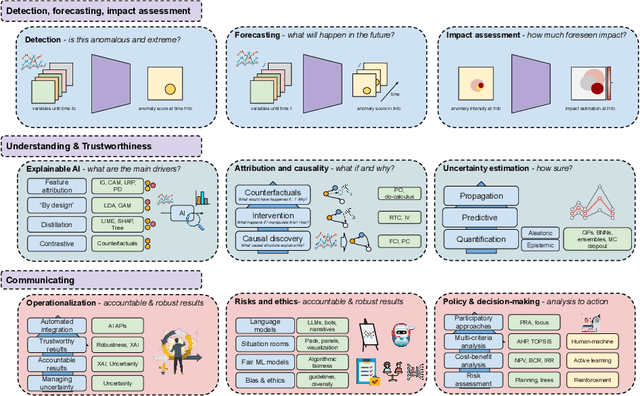
In recent years, artificial intelligence (AI) has deeply impacted various fields, including Earth system sciences. Here, AI improved weather forecasting, model emulation, parameter estimation, and the prediction of extreme events. However, the latter comes with specific challenges, such as developing accurate predictors from noisy, heterogeneous and limited annotated data. This paper reviews how AI is being used to analyze extreme events (like floods, droughts, wildfires and heatwaves), highlighting the importance of creating accurate, transparent, and reliable AI models. We discuss the hurdles of dealing with limited data, integrating information in real-time, deploying models, and making them understandable, all crucial for gaining the trust of stakeholders and meeting regulatory needs. We provide an overview of how AI can help identify and explain extreme events more effectively, improving disaster response and communication. We emphasize the need for collaboration across different fields to create AI solutions that are practical, understandable, and trustworthy for analyzing and predicting extreme events. Such collaborative efforts aim to enhance disaster readiness and disaster risk reduction.

Online Calibration of Deep Learning Sub-Models for Hybrid Numerical Modeling Systems

Artificial intelligence and deep learning are currently reshaping numerical simulation frameworks by introducing new modeling capabilities. These frameworks are extensively investigated in the context of model correction and parameterization where they demonstrate great potential and often outperform traditional physical models. Most of these efforts in defining hybrid dynamical systems follow {offline} learning strategies in which the neural parameterization (called here sub-model) is trained to output an ideal correction. Yet, these hybrid models can face hard limitations when defining what should be a relevant sub-model response that would translate into a good forecasting performance. End-to-end learning schemes, also referred to as online learning, could address such a shortcoming by allowing the deep learning sub-models to train on historical data. However, defining end-to-end training schemes for the calibration of neural sub-models in hybrid systems requires working with an optimization problem that involves the solver of the physical equations. Online learning methodologies thus require the numerical model to be differentiable, which is not the case for most modeling systems. To overcome this difficulty and bypass the differentiability challenge of physical models, we present an efficient and practical online learning approach for hybrid systems. The method, called EGA for Euler Gradient Approximation, assumes an additive neural correction to the physical model, and an explicit Euler approximation of the gradients. We demonstrate that the EGA converges to the exact gradients in the limit of infinitely small time steps. Numerical experiments are performed on various case studies, including prototypical ocean-atmosphere dynamics. Results show significant improvements over offline learning, highlighting the potential of end-to-end online learning for hybrid modeling.

Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review

Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.

Bounded nonlinear forecasts of partially observed geophysical systems with physics-constrained deep learning

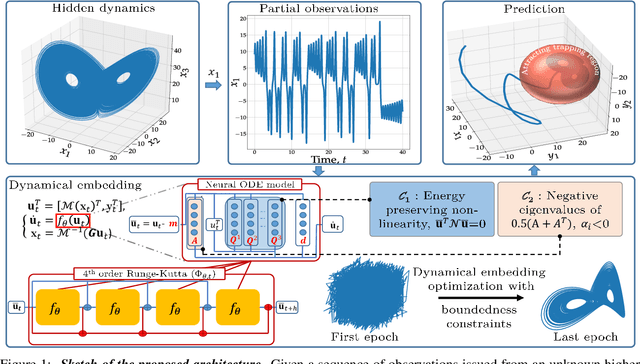
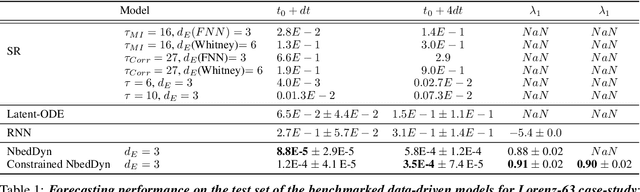
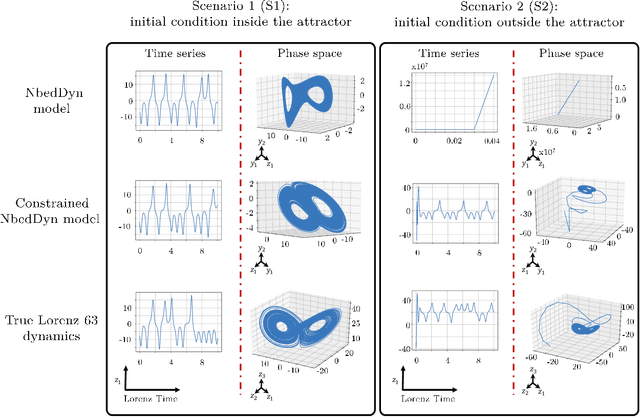
The complexity of real-world geophysical systems is often compounded by the fact that the observed measurements depend on hidden variables. These latent variables include unresolved small scales and/or rapidly evolving processes, partially observed couplings, or forcings in coupled systems. This is the case in ocean-atmosphere dynamics, for which unknown interior dynamics can affect surface observations. The identification of computationally-relevant representations of such partially-observed and highly nonlinear systems is thus challenging and often limited to short-term forecast applications. Here, we investigate the physics-constrained learning of implicit dynamical embeddings, leveraging neural ordinary differential equation (NODE) representations. A key objective is to constrain their boundedness, which promotes the generalization of the learned dynamics to arbitrary initial condition. The proposed architecture is implemented within a deep learning framework, and its relevance is demonstrated with respect to state-of-the-art schemes for different case-studies representative of geophysical dynamics.

Learning Runge-Kutta Integration Schemes for ODE Simulation and Identification

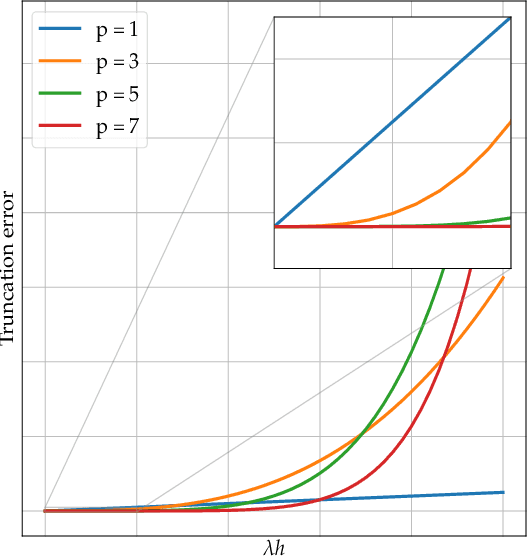
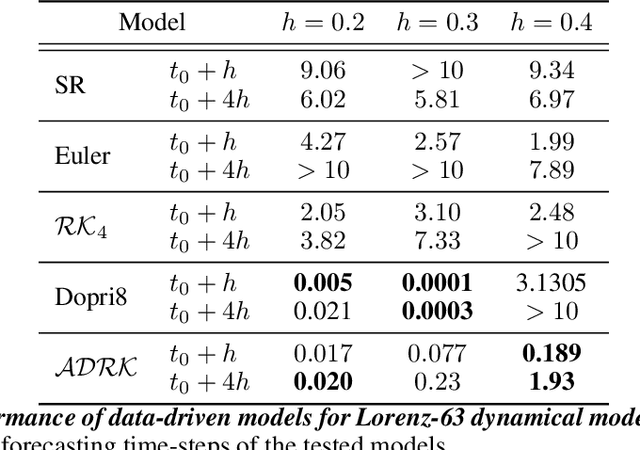
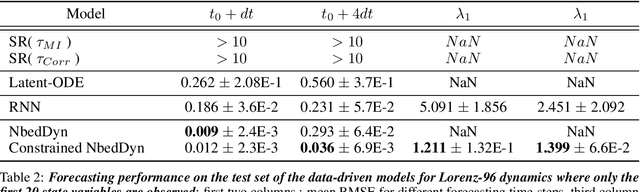
Deriving analytical solutions of ordinary differential equations is usually restricted to a small subset of problems and numerical techniques are considered. Inevitably, a numerical simulation of a differential equation will then always be distinct from a true analytical solution. An efficient integration scheme shall further not only provide a trajectory throughout a given state, but also be derived to ensure the generated simulation to be close to the analytical one. Consequently, several integration schemes were developed for different classes of differential equations. Unfortunately, when considering the integration of complex non-linear systems, as well as the identification of non-linear equations from data, this choice of the integration scheme is often far from being trivial. In this paper, we propose a novel framework to learn integration schemes that minimize an integration-related cost function. We demonstrate the relevance of the proposed learning-based approach for non-linear equations and include a quantitative analysis w.r.t. classical state-of-the-art integration techniques, especially where the latter may not apply.

Variational Deep Learning for the Identification and Reconstruction of Chaotic and Stochastic Dynamical Systems from Noisy and Partial Observations

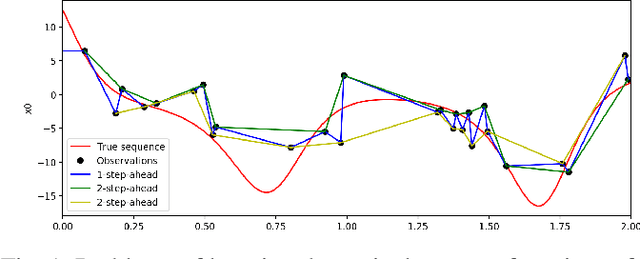
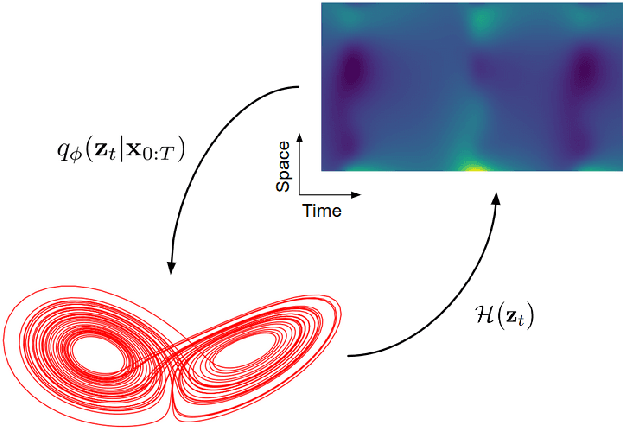
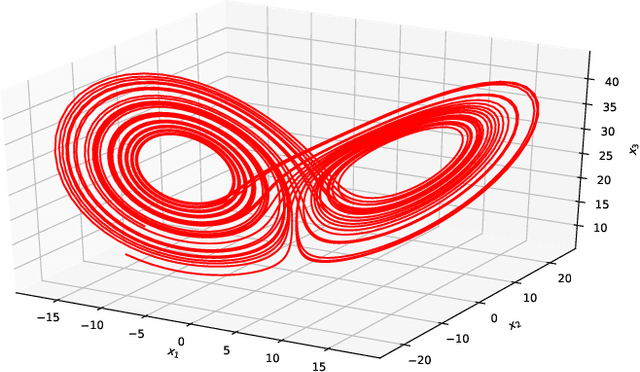
The data-driven recovery of the unknown governing equations of dynamical systems has recently received an increasing interest. However, the identification of the governing equations remains challenging when dealing with noisy and partial observations. Here, we address this challenge and investigate variational deep learning schemes. Within the proposed framework, we jointly learn an inference model to reconstruct the true states of the system from series of noisy and partial data and the governing equations of these states. In doing so, this framework bridges classical data assimilation and state-of-the-art machine learning techniques and we show that it generalizes state-of-the-art methods. Importantly, both the inference model and the governing equations embed stochastic components to account for stochastic variabilities, model errors and reconstruction uncertainties. Various experiments on chaotic and stochastic dynamical systems support the relevance of our scheme w.r.t. state-of-the-art approaches.

Learning Latent Dynamics for Partially-Observed Chaotic Systems

This paper addresses the data-driven identification of latent dynamical representations of partially-observed systems, i.e., dynamical systems for which some components are never observed, with an emphasis on forecasting applications, including long-term asymptotic patterns. Whereas state-of-the-art data-driven approaches rely on delay embeddings and linear decompositions of the underlying operators, we introduce a framework based on the data-driven identification of an augmented state-space model using a neural-network-based representation. For a given training dataset, it amounts to jointly learn an ODE (Ordinary Differential Equation) representation in the latent space and reconstructing latent states. Through numerical experiments, we demonstrate the relevance of the proposed framework w.r.t. state-of-the-art approaches in terms of short-term forecasting performance and long-term behaviour. We further discuss how the proposed framework relates to Koopman operator theory and Takens' embedding theorem.

EM-like Learning Chaotic Dynamics from Noisy and Partial Observations

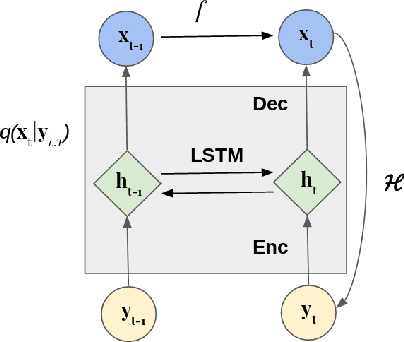
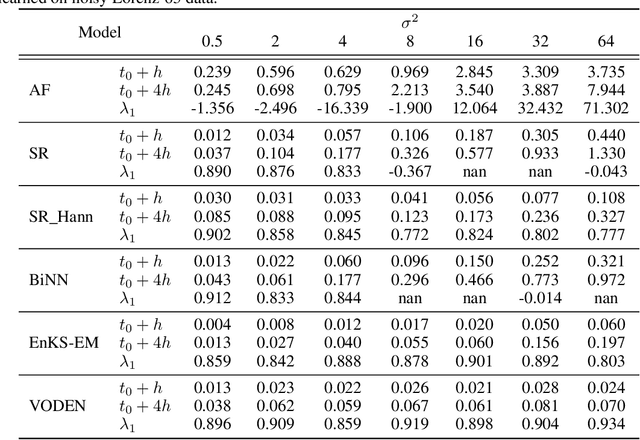
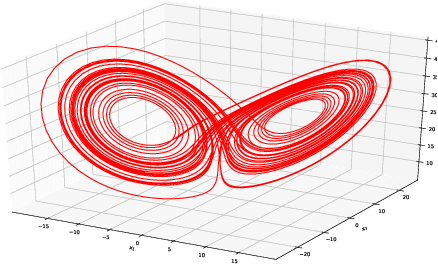
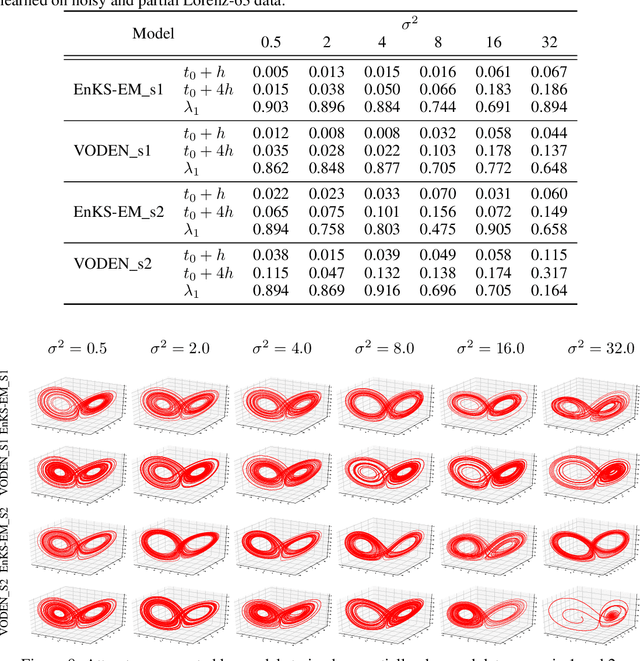
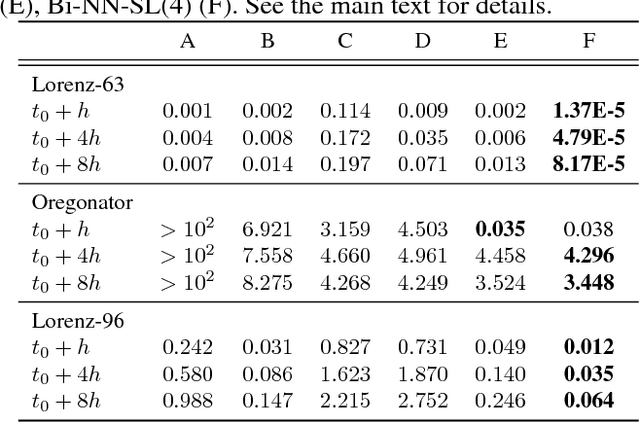
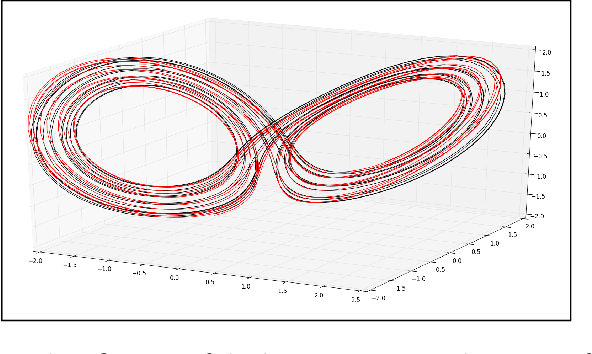
The identification of the governing equations of chaotic dynamical systems from data has recently emerged as a hot topic. While the seminal work by Brunton et al. reported proof-of-concepts for idealized observation setting for fully-observed systems, {\em i.e.} large signal-to-noise ratios and high-frequency sampling of all system variables, we here address the learning of data-driven representations of chaotic dynamics for partially-observed systems, including significant noise patterns and possibly lower and irregular sampling setting. Instead of considering training losses based on short-term prediction error like state-of-the-art learning-based schemes, we adopt a Bayesian formulation and state this issue as a data assimilation problem with unknown model parameters. To solve for the joint inference of the hidden dynamics and of model parameters, we combine neural-network representations and state-of-the-art assimilation schemes. Using iterative Expectation-Maximization (EM)-like procedures, the key feature of the proposed inference schemes is the derivation of the posterior of the hidden dynamics. Using a neural-network-based Ordinary Differential Equation (ODE) representation of these dynamics, we investigate two strategies: their combination to Ensemble Kalman Smoothers and Long Short-Term Memory (LSTM)-based variational approximations of the posterior. Through numerical experiments on the Lorenz-63 system with different noise and time sampling settings, we demonstrate the ability of the proposed schemes to recover and reproduce the hidden chaotic dynamics, including their Lyapunov characteristic exponents, when classic machine learning approaches fail.

Sea surface temperature prediction and reconstruction using patch-level neural network representations

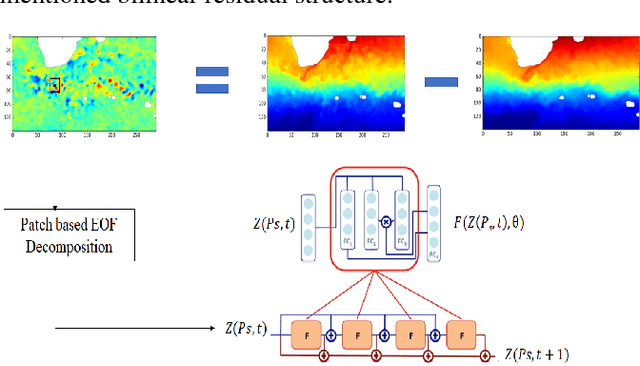
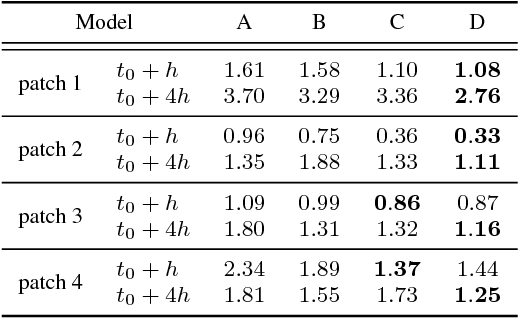
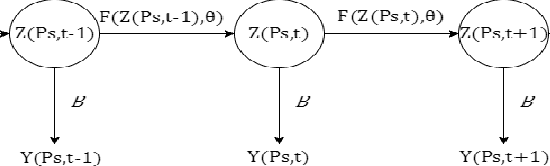
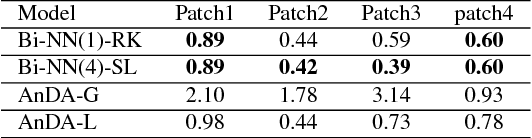
The forecasting and reconstruction of ocean and atmosphere dynamics from satellite observation time series are key challenges. While model-driven representations remain the classic approaches, data-driven representations become more and more appealing to benefit from available large-scale observation and simulation datasets. In this work we investigate the relevance of recently introduced bilinear residual neural network representations, which mimic numerical integration schemes such as Runge-Kutta, for the forecasting and assimilation of geophysical fields from satellite-derived remote sensing data. As a case-study, we consider satellite-derived Sea Surface Temperature time series off South Africa, which involves intense and complex upper ocean dynamics. Our numerical experiments demonstrate that the proposed patch-level neural-network-based representations outperform other data-driven models, including analog schemes, both in terms of forecasting and missing data interpolation performance with a relative gain up to 50\% for highly dynamic areas.

Bilinear residual Neural Network for the identification and forecasting of dynamical systems

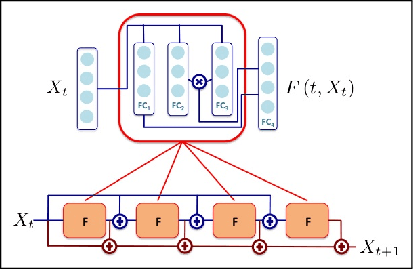
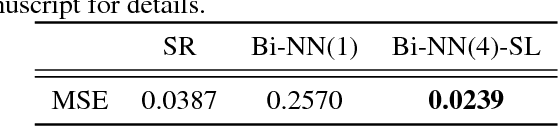
Due to the increasing availability of large-scale observation and simulation datasets, data-driven representations arise as efficient and relevant computation representations of dynamical systems for a wide range of applications, where model-driven models based on ordinary differential equation remain the state-of-the-art approaches. In this work, we investigate neural networks (NN) as physically-sound data-driven representations of such systems. Reinterpreting Runge-Kutta methods as graphical models, we consider a residual NN architecture and introduce bilinear layers to embed non-linearities which are intrinsic features of dynamical systems. From numerical experiments for classic dynamical systems, we demonstrate the relevance of the proposed NN-based architecture both in terms of forecasting performance and model identification.