Bilinear residual Neural Network for the identification and forecasting of dynamical systems
Paper and Code
Dec 19, 2017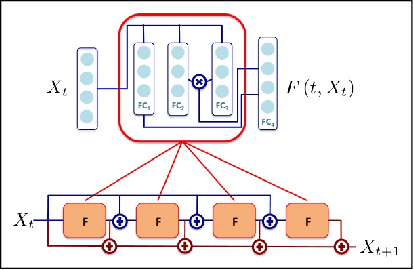
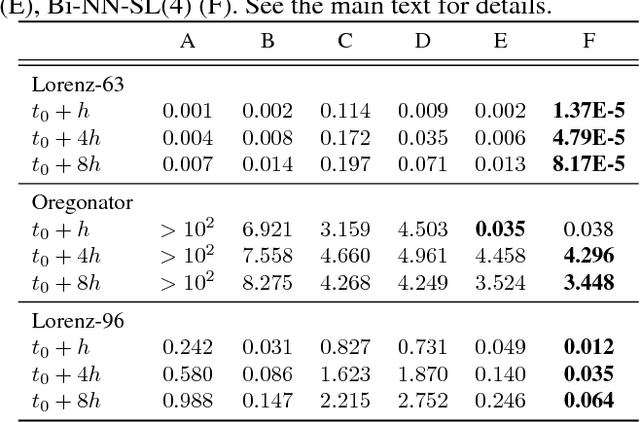
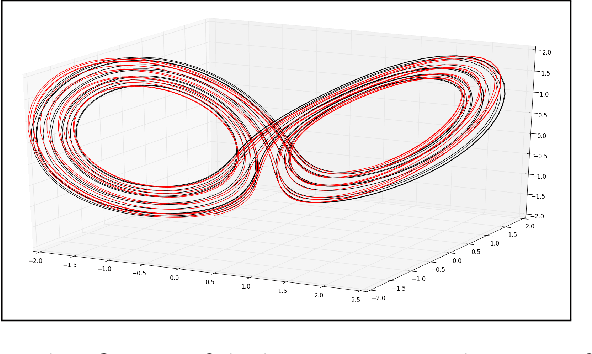
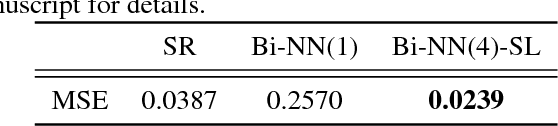
Due to the increasing availability of large-scale observation and simulation datasets, data-driven representations arise as efficient and relevant computation representations of dynamical systems for a wide range of applications, where model-driven models based on ordinary differential equation remain the state-of-the-art approaches. In this work, we investigate neural networks (NN) as physically-sound data-driven representations of such systems. Reinterpreting Runge-Kutta methods as graphical models, we consider a residual NN architecture and introduce bilinear layers to embed non-linearities which are intrinsic features of dynamical systems. From numerical experiments for classic dynamical systems, we demonstrate the relevance of the proposed NN-based architecture both in terms of forecasting performance and model identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge