Variational Deep Learning for the Identification and Reconstruction of Chaotic and Stochastic Dynamical Systems from Noisy and Partial Observations

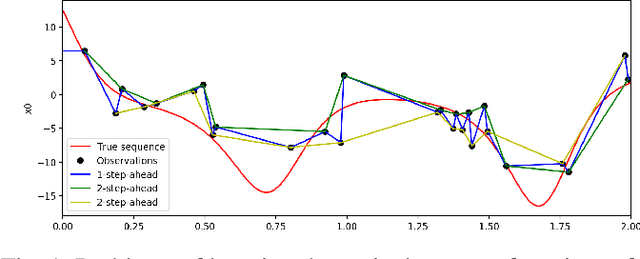
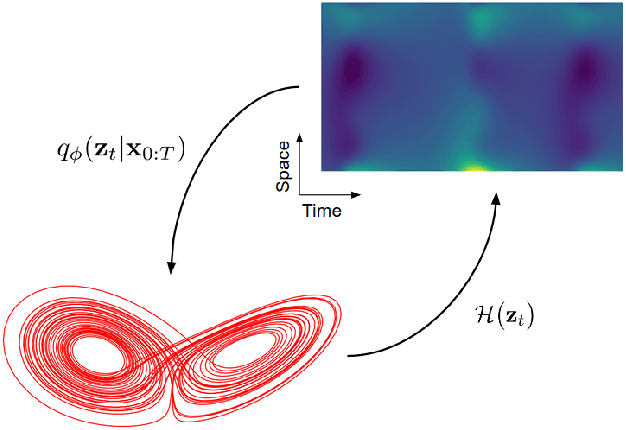
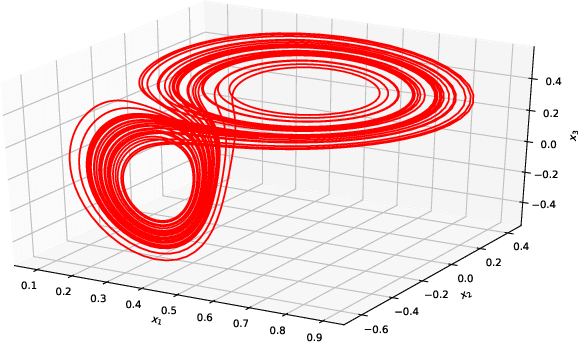
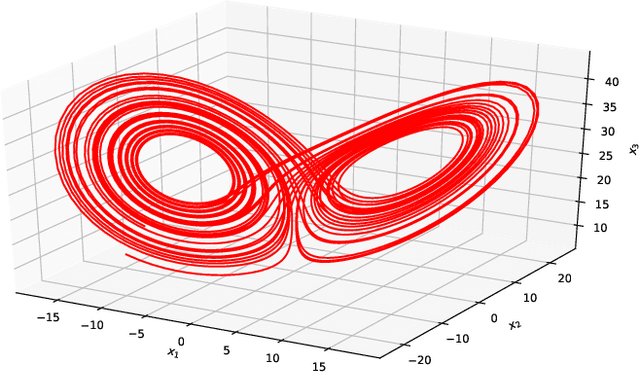
The data-driven recovery of the unknown governing equations of dynamical systems has recently received an increasing interest. However, the identification of the governing equations remains challenging when dealing with noisy and partial observations. Here, we address this challenge and investigate variational deep learning schemes. Within the proposed framework, we jointly learn an inference model to reconstruct the true states of the system from series of noisy and partial data and the governing equations of these states. In doing so, this framework bridges classical data assimilation and state-of-the-art machine learning techniques and we show that it generalizes state-of-the-art methods. Importantly, both the inference model and the governing equations embed stochastic components to account for stochastic variabilities, model errors and reconstruction uncertainties. Various experiments on chaotic and stochastic dynamical systems support the relevance of our scheme w.r.t. state-of-the-art approaches.