Towards diffusion models for large-scale sea-ice modelling

We make the first steps towards diffusion models for unconditional generation of multivariate and Arctic-wide sea-ice states. While targeting to reduce the computational costs by diffusion in latent space, latent diffusion models also offer the possibility to integrate physical knowledge into the generation process. We tailor latent diffusion models to sea-ice physics with a censored Gaussian distribution in data space to generate data that follows the physical bounds of the modelled variables. Our latent diffusion models reach similar scores as the diffusion model trained in data space, but they smooth the generated fields as caused by the latent mapping. While enforcing physical bounds cannot reduce the smoothing, it improves the representation of the marginal ice zone. Therefore, for large-scale Earth system modelling, latent diffusion models can have many advantages compared to diffusion in data space if the significant barrier of smoothing can be resolved.

Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review

Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.

Learning 4DVAR inversion directly from observations

Variational data assimilation and deep learning share many algorithmic aspects in common. While the former focuses on system state estimation, the latter provides great inductive biases to learn complex relationships. We here design a hybrid architecture learning the assimilation task directly from partial and noisy observations, using the mechanistic constraint of the 4DVAR algorithm. Finally, we show in an experiment that the proposed method was able to learn the desired inversion with interesting regularizing properties and that it also has computational interests.

Super-resolution data assimilation

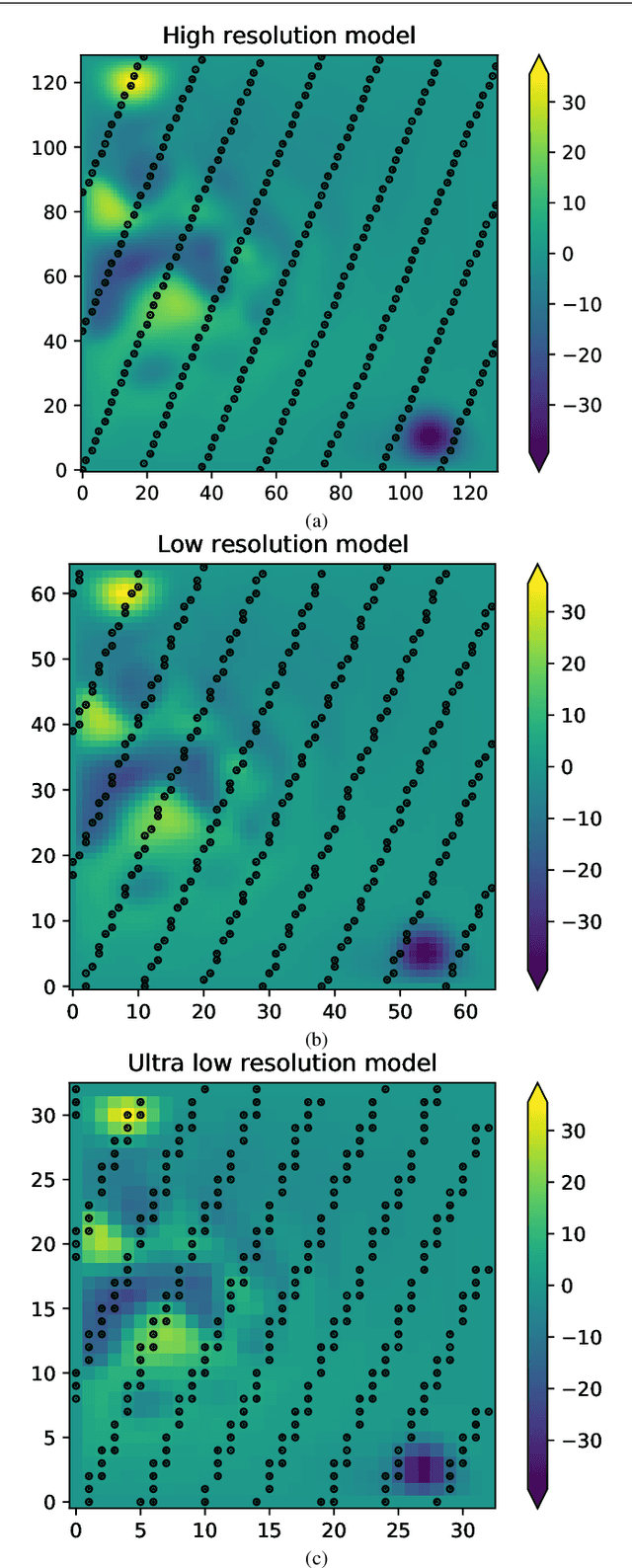
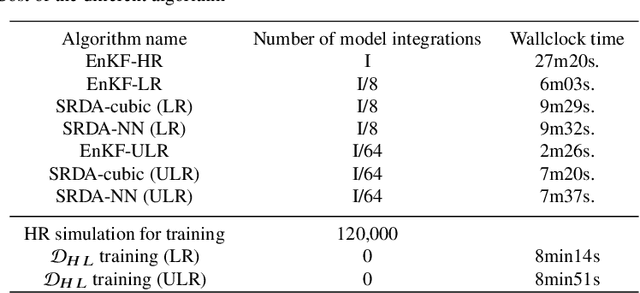
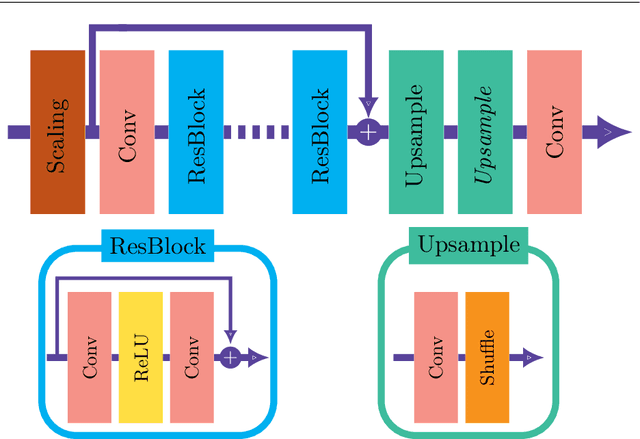
Increasing the resolution of a model can improve the performance of a data assimilation system: first because model field are in better agreement with high resolution observations, then the corrections are better sustained and, with ensemble data assimilation, the forecast error covariances are improved. However, resolution increase is associated with a cubical increase of the computational costs. Here we are testing an approach inspired from images super-resolution techniques and called "Super-resolution data assimilation" (SRDA). Starting from a low-resolution forecast, a neural network (NN) emulates a high-resolution field that is then used to assimilate high-resolution observations. We apply the SRDA to a quasi-geostrophic model representing simplified surface ocean dynamics, with a model resolution up to four times lower than the reference high-resolution and we use the Ensemble Kalman Filter data assimilation method. We show that SRDA outperforms the low-resolution data assimilation approach and a SRDA version with cubic spline interpolation instead of NN. The NN's ability to anticipate the systematic differences between low and high resolution model dynamics explains the enhanced performance, for example by correcting the difference of propagation speed of eddies. Increasing the computational cost by 55\% above the LR data assimilation system (using a 25-members ensemble), the SRDA reduces the errors by 40\% making the performance very close to the HR system (16\% larger, compared to 92\% larger for the LR EnKF). The reliability of the ensemble system is not degraded by SRDA.

Bridging observation, theory and numerical simulation of the ocean using Machine Learning

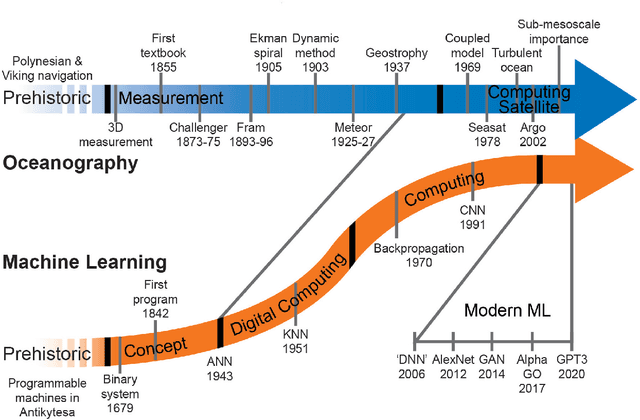
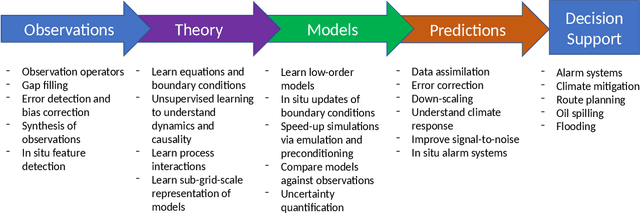
Progress within physical oceanography has been concurrent with the increasing sophistication of tools available for its study. The incorporation of machine learning (ML) techniques offers exciting possibilities for advancing the capacity and speed of established methods and also for making substantial and serendipitous discoveries. Beyond vast amounts of complex data ubiquitous in many modern scientific fields, the study of the ocean poses a combination of unique challenges that ML can help address. The observational data available is largely spatially sparse, limited to the surface, and with few time series spanning more than a handful of decades. Important timescales span seconds to millennia, with strong scale interactions and numerical modelling efforts complicated by details such as coastlines. This review covers the current scientific insight offered by applying ML and points to where there is imminent potential. We cover the main three branches of the field: observations, theory, and numerical modelling. Highlighting both challenges and opportunities, we discuss both the historical context and salient ML tools. We focus on the use of ML in situ sampling and satellite observations, and the extent to which ML applications can advance theoretical oceanographic exploration, as well as aid numerical simulations. Applications that are also covered include model error and bias correction and current and potential use within data assimilation. While not without risk, there is great interest in the potential benefits of oceanographic ML applications; this review caters to this interest within the research community.

Fusion of rain radar images and wind forecasts in a deep learning model applied to rain nowcasting

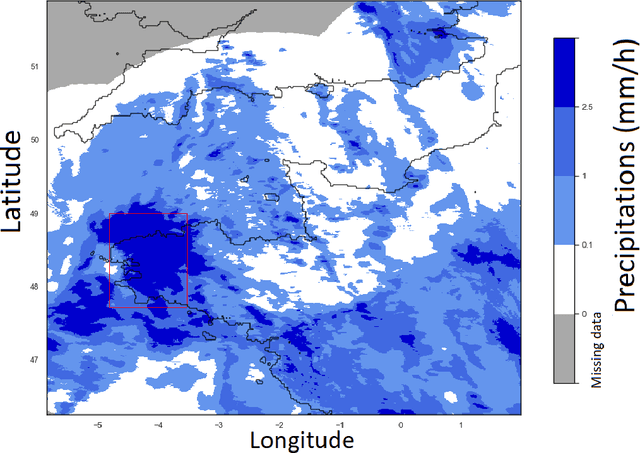
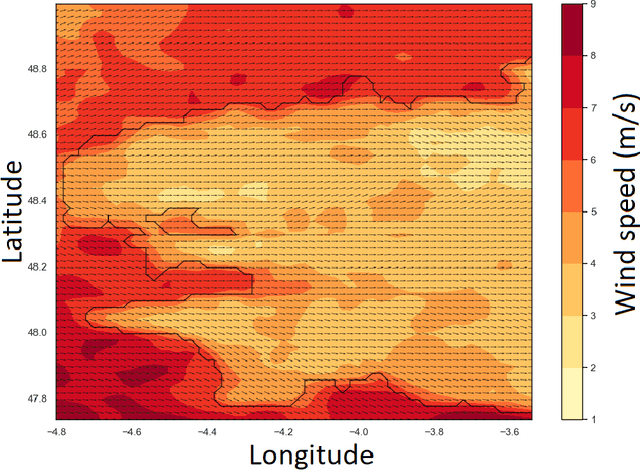
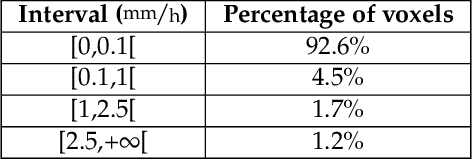
Short- or mid-term rainfall forecasting is a major task with several environmental applications such as agricultural management or flood risk monitoring. Existing data-driven approaches, especially deep learning models, have shown significant skill at this task, using only rainfall radar images as inputs. In order to determine whether using other meteorological parameters such as wind would improve forecasts, we trained a deep learning model on a fusion of rainfall radar images and wind velocity produced by a weather forecast model. The network was compared to a similar architecture trained only on radar data, to a basic persistence model and to an approach based on optical flow. Our network outperforms by 8% the F1-score calculated for the optical flow on moderate and higher rain events for forecasts at a horizon time of 30 min. Furthermore, it outperforms by 7% the same architecture trained using only rainfall radar images. Merging rain and wind data has also proven to stabilize the training process and enabled significant improvement especially on the difficult-to-predict high precipitation rainfalls.

Combining data assimilation and machine learning to infer unresolved scale parametrisation

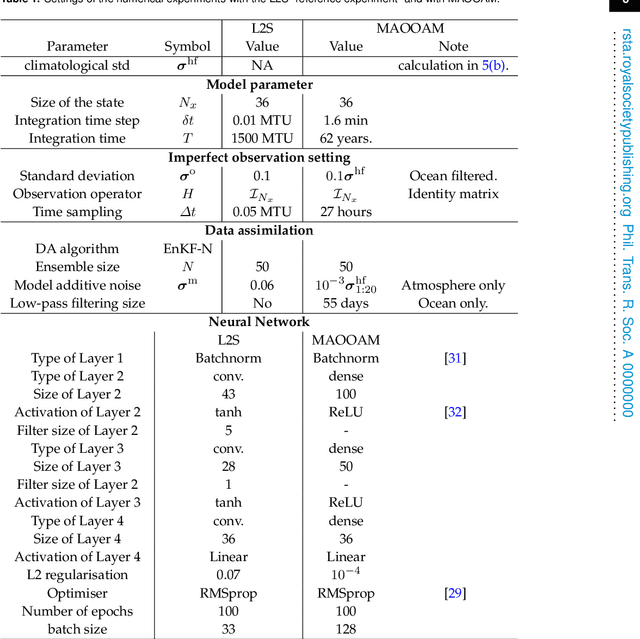
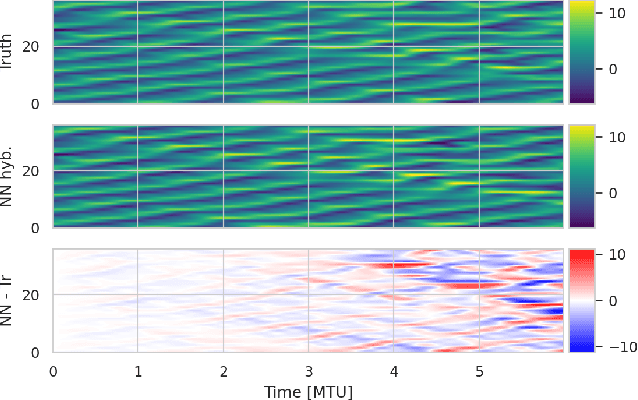
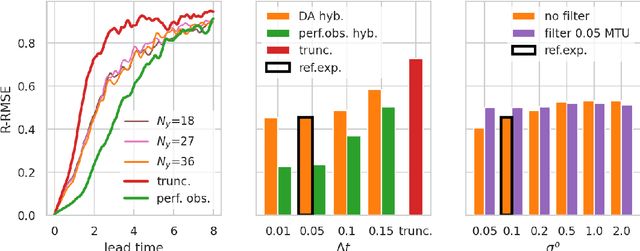
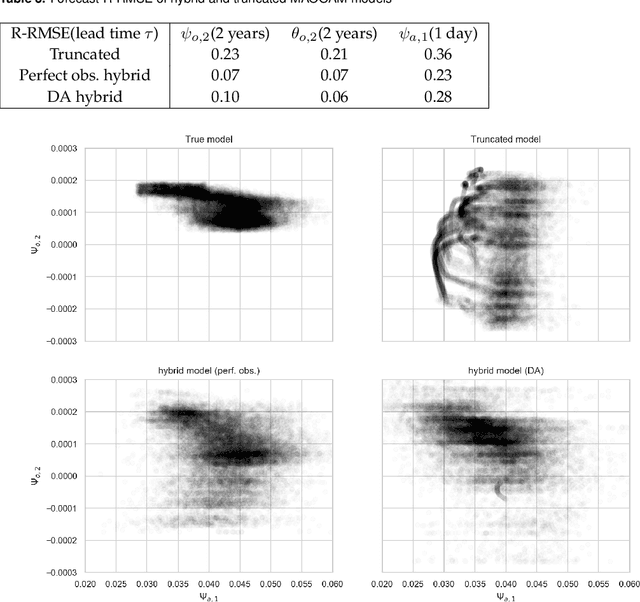
In recent years, machine learning (ML) has been proposed to devise data-driven parametrisations of unresolved processes in dynamical numerical models. In most cases, the ML training leverages high-resolution simulations to provide a dense, noiseless target state. Our goal is to go beyond the use of high-resolution simulations and train ML-based parametrisation using direct data, in the realistic scenario of noisy and sparse observations. The algorithm proposed in this work is a two-step process. First, data assimilation (DA) techniques are applied to estimate the full state of the system from a truncated model. The unresolved part of the truncated model is viewed as a model error in the DA system. In a second step, ML is used to emulate the unresolved part, a predictor of model error given the state of the system. Finally, the ML-based parametrisation model is added to the physical core truncated model to produce a hybrid model.

Bayesian inference of dynamics from partial and noisy observations using data assimilation and machine learning

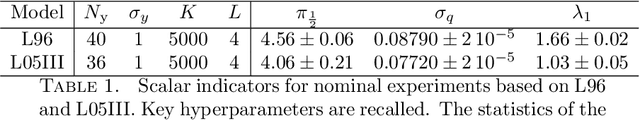
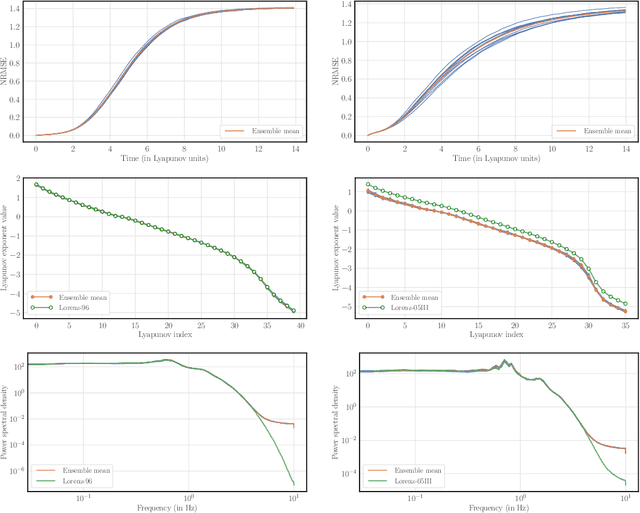
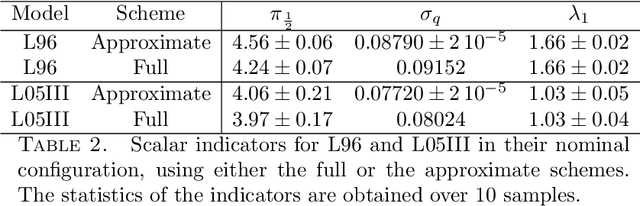
The reconstruction from observations of high-dimensional chaotic dynamics such as geophysical flows is hampered by (i) the partial and noisy observations that can realistically be obtained, (ii) the need to learn from long time series of data, and (iii) the unstable nature of the dynamics. To achieve such inference from the observations over long time series, it has been suggested to combine data assimilation and machine learning in several ways. We show how to unify these approaches from a Bayesian perspective using expectation-maximization and coordinate descents. Implementations and approximations of these methods are also discussed. Finally, we numerically and successfully test the approach on two relevant low-order chaotic models with distinct identifiability.

Combining data assimilation and machine learning to emulate a dynamical model from sparse and noisy observations: a case study with the Lorenz 96 model

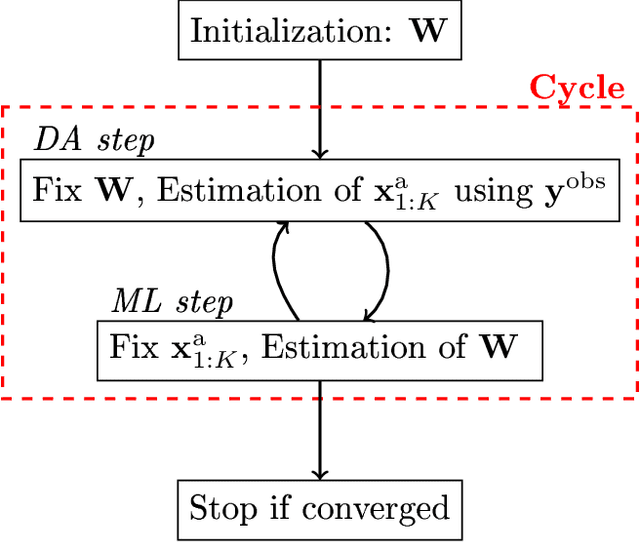
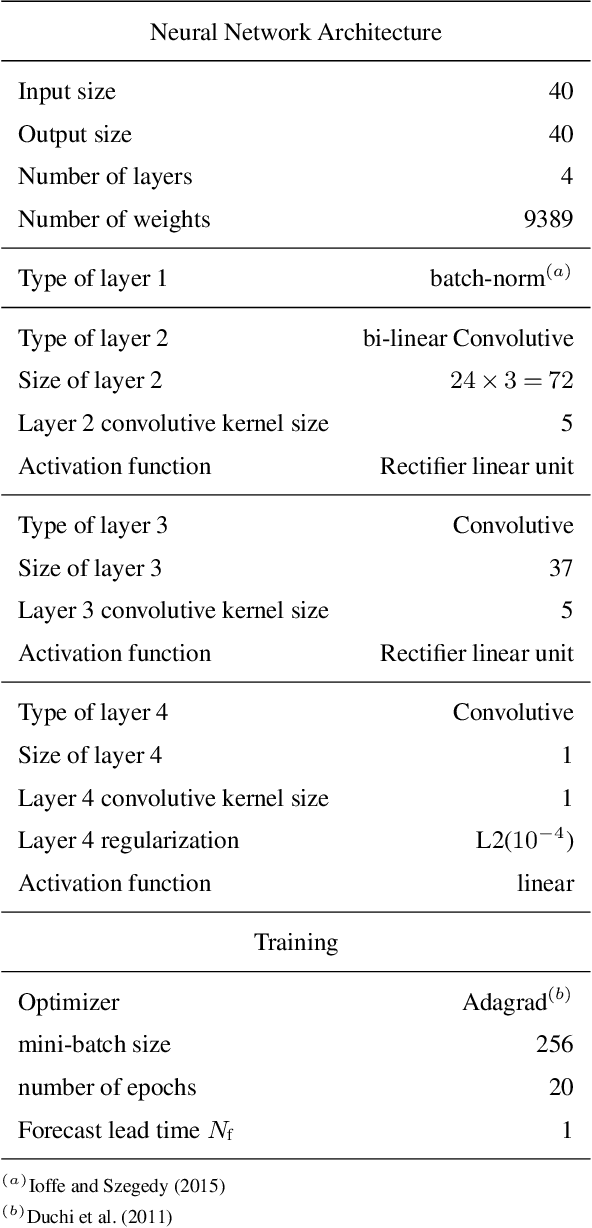
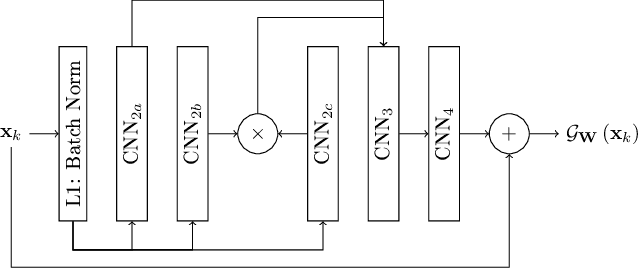
A novel method, based on the combination of data assimilation and machine learning is introduced. The new hybrid approach is designed for a two-fold scope: (i) emulating hidden, possibly chaotic, dynamics and (ii) predicting their future states. The method consists in applying iteratively a data assimilation step, here an ensemble Kalman filter, and a neural network. Data assimilation is used to optimally combine a surrogate model with sparse noisy data. The output analysis is spatially complete and is used as a training set by the neural network to update the surrogate model. The two steps are then repeated iteratively. Numerical experiments have been carried out using the chaotic 40-variables Lorenz 96 model, proving both convergence and statistical skills of the proposed hybrid approach. The surrogate model shows short-term forecast skills up to two Lyapunov times, the retrieval of positive Lyapunov exponents as well as the more energetic frequencies of the power density spectrum. The sensitivity of the method to critical setup parameters is also presented: forecast skills decrease smoothly with increased observational noise but drops abruptly if less than half of the model domain is observed. The successful synergy between data assimilation and machine learning, proven here with a low-dimensional system, encourages further investigation of such hybrids with more sophisticated dynamics.

Representing ill-known parts of a numerical model using a machine learning approach

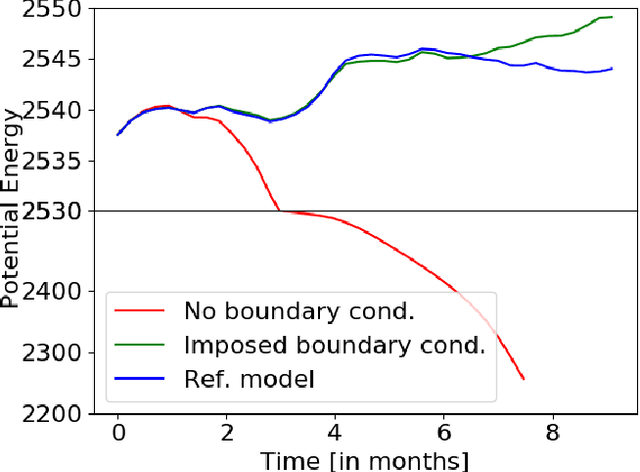
In numerical modeling of the Earth System, many processes remain unknown or ill represented (let us quote sub-grid processes, the dependence to unknown latent variables or the non-inclusion of complex dynamics in numerical models) but sometimes can be observed. This paper proposes a methodology to produce a hybrid model combining a physical-based model (forecasting the well-known processes) with a neural-net model trained from observations (forecasting the remaining processes). The approach is applied to a shallow-water model in which the forcing, dissipative and diffusive terms are assumed to be unknown. We show that the hybrid model is able to reproduce with great accuracy the unknown terms (correlation close to 1). For long term simulations it reproduces with no significant difference the mean state, the kinetic energy, the potential energy and the potential vorticity of the system. Lastly it is able to function with new forcings that were not encountered during the training phase of the neural network.