Tobias Sebastian Finn
Generative AI models enable efficient and physically consistent sea-ice simulations
Aug 20, 2025

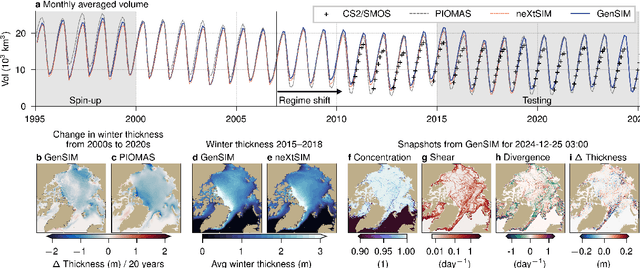

Abstract:Sea ice is governed by highly complex, scale-invariant, and anisotropic processes that are challenging to represent in Earth system models. While advanced numerical models have improved our understanding of the sea-ice dynamics, their computational costs often limit their application in ensemble forecasting and climate simulations. Here, we introduce GenSIM, the first generative AI-based pan-Arctic model that predicts the evolution of all relevant key properties, including concentration, thickness, and drift, in a 12-hour window with improved accuracy over deterministic predictions and high computational efficiency, while remaining physically consistent. Trained on a long simulation from a state-of-the-art sea-ice--ocean system, GenSIM robustly reproduces statistics as observed in numerical models and observations, exhibiting brittle-like short-term dynamics while also depicting the long-term sea-ice decline. Driven solely by atmospheric forcings, we attribute GenSIM's emergent extrapolation capabilities to patterns that reflect the long-term impact of the ocean: it seemingly has learned an internal ocean emulator. This ability to infer slowly evolving climate-relevant dynamics from short-term predictions underlines the large potential of generative models to generalise for unseen climates and to encode hidden physics.
Ensemble Kalman filter in latent space using a variational autoencoder pair
Feb 18, 2025



Abstract:Popular (ensemble) Kalman filter data assimilation (DA) approaches assume that the errors in both the a priori estimate of the state and those in the observations are Gaussian. For constrained variables, e.g. sea ice concentration or stress, such an assumption does not hold. The variational autoencoder (VAE) is a machine learning (ML) technique that allows to map an arbitrary distribution to/from a latent space in which the distribution is supposedly closer to a Gaussian. We propose a novel hybrid DA-ML approach in which VAEs are incorporated in the DA procedure. Specifically, we introduce a variant of the popular ensemble transform Kalman filter (ETKF) in which the analysis is applied in the latent space of a single VAE or a pair of VAEs. In twin experiments with a simple circular model, whereby the circle represents an underlying submanifold to be respected, we find that the use of a VAE ensures that a posteri ensemble members lie close to the manifold containing the truth. Furthermore, online updating of the VAE is necessary and achievable when this manifold varies in time, i.e. when it is non-stationary. We demonstrate that introducing an additional second latent space for the observational innovations improves robustness against detrimental effects of non-Gaussianity and bias in the observational errors but it slightly lessens the performance if observational errors are strictly Gaussian.
Machine learning for modelling unstructured grid data in computational physics: a review
Feb 13, 2025
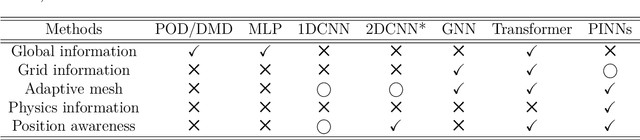
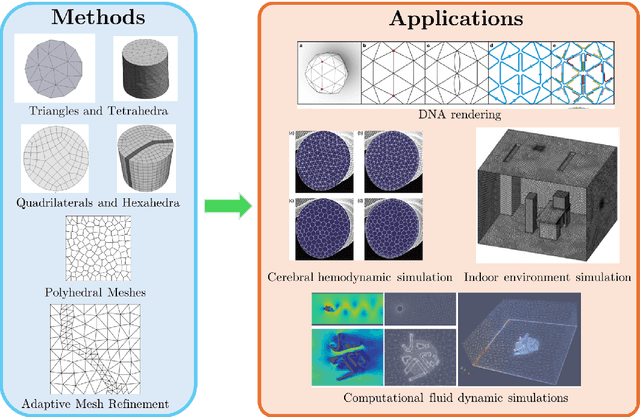

Abstract:Unstructured grid data are essential for modelling complex geometries and dynamics in computational physics. Yet, their inherent irregularity presents significant challenges for conventional machine learning (ML) techniques. This paper provides a comprehensive review of advanced ML methodologies designed to handle unstructured grid data in high-dimensional dynamical systems. Key approaches discussed include graph neural networks, transformer models with spatial attention mechanisms, interpolation-integrated ML methods, and meshless techniques such as physics-informed neural networks. These methodologies have proven effective across diverse fields, including fluid dynamics and environmental simulations. This review is intended as a guidebook for computational scientists seeking to apply ML approaches to unstructured grid data in their domains, as well as for ML researchers looking to address challenges in computational physics. It places special focus on how ML methods can overcome the inherent limitations of traditional numerical techniques and, conversely, how insights from computational physics can inform ML development. To support benchmarking, this review also provides a summary of open-access datasets of unstructured grid data in computational physics. Finally, emerging directions such as generative models with unstructured data, reinforcement learning for mesh generation, and hybrid physics-data-driven paradigms are discussed to inspire future advancements in this evolving field.
Self-attentive Transformer for Fast and Accurate Postprocessing of Temperature and Wind Speed Forecasts
Dec 18, 2024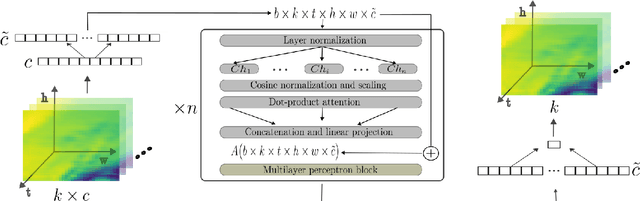
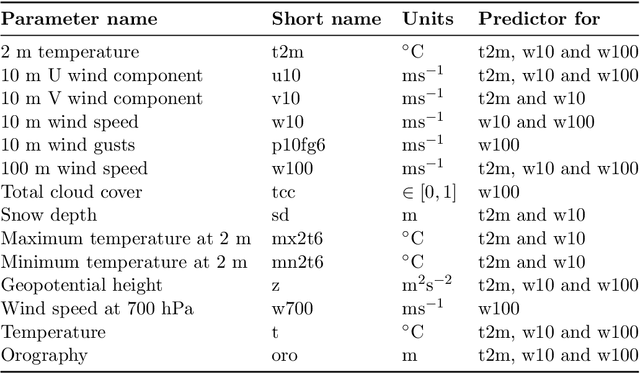
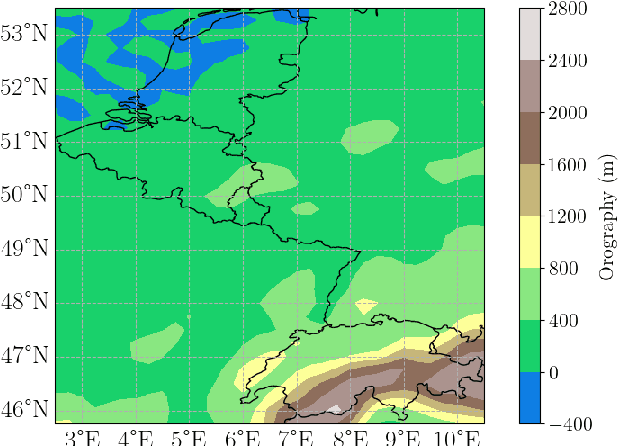

Abstract:Current postprocessing techniques often require separate models for each lead time and disregard possible inter-ensemble relationships by either correcting each member separately or by employing distributional approaches. In this work, we tackle these shortcomings with an innovative, fast and accurate Transformer which postprocesses each ensemble member individually while allowing information exchange across variables, spatial dimensions and lead times by means of multi-headed self-attention. Weather foreacasts are postprocessed over 20 lead times simultaneously while including up to twelve meteorological predictors. We use the EUPPBench dataset for training which contains ensemble predictions from the European Center for Medium-range Weather Forecasts' integrated forecasting system alongside corresponding observations. The work presented here is the first to postprocess the ten and one hundred-meter wind speed forecasts within this benchmark dataset, while also correcting the two-meter temperature. Our approach significantly improves the original forecasts, as measured by the CRPS, with 17.5 % for two-meter temperature, nearly 5% for ten-meter wind speed and 5.3 % for one hundred-meter wind speed, outperforming a classical member-by-member approach employed as competitive benchmark. Furthermore, being up to 75 times faster, it fulfills the demand for rapid operational weather forecasts in various downstream applications, including renewable energy forecasting.
Towards diffusion models for large-scale sea-ice modelling
Jun 26, 2024



Abstract:We make the first steps towards diffusion models for unconditional generation of multivariate and Arctic-wide sea-ice states. While targeting to reduce the computational costs by diffusion in latent space, latent diffusion models also offer the possibility to integrate physical knowledge into the generation process. We tailor latent diffusion models to sea-ice physics with a censored Gaussian distribution in data space to generate data that follows the physical bounds of the modelled variables. Our latent diffusion models reach similar scores as the diffusion model trained in data space, but they smooth the generated fields as caused by the latent mapping. While enforcing physical bounds cannot reduce the smoothing, it improves the representation of the marginal ice zone. Therefore, for large-scale Earth system modelling, latent diffusion models can have many advantages compared to diffusion in data space if the significant barrier of smoothing can be resolved.
Self-Attentive Ensemble Transformer: Representing Ensemble Interactions in Neural Networks for Earth System Models
Jul 10, 2021
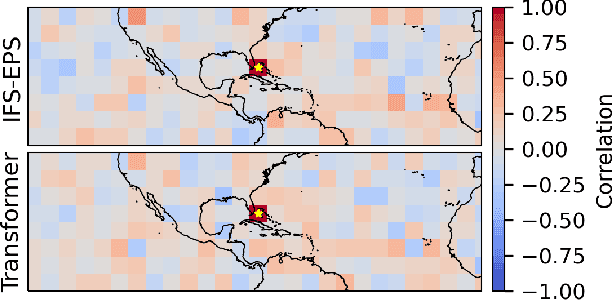


Abstract:Ensemble data from Earth system models has to be calibrated and post-processed. I propose a novel member-by-member post-processing approach with neural networks. I bridge ideas from ensemble data assimilation with self-attention, resulting into the self-attentive ensemble transformer. Here, interactions between ensemble members are represented as additive and dynamic self-attentive part. As proof-of-concept, I regress global ECMWF ensemble forecasts to 2-metre-temperature fields from the ERA5 reanalysis. I demonstrate that the ensemble transformer can calibrate the ensemble spread and extract additional information from the ensemble. As it is a member-by-member approach, the ensemble transformer directly outputs multivariate and spatially-coherent ensemble members. Therefore, self-attention and the transformer technique can be a missing piece for a non-parametric post-processing of ensemble data with neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge