Marc Bocquet
CEREA, joint laboratory École des Ponts ParisTech and EDF R&D, Université Paris-Est, Champs-sur-Marne, France
Generative AI models enable efficient and physically consistent sea-ice simulations
Aug 20, 2025

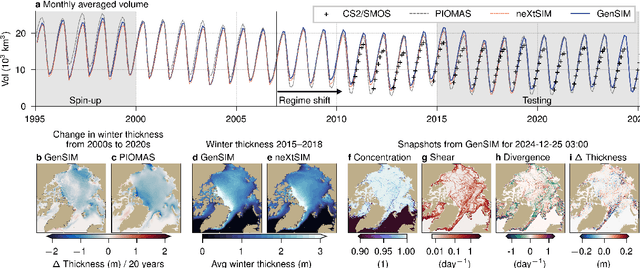
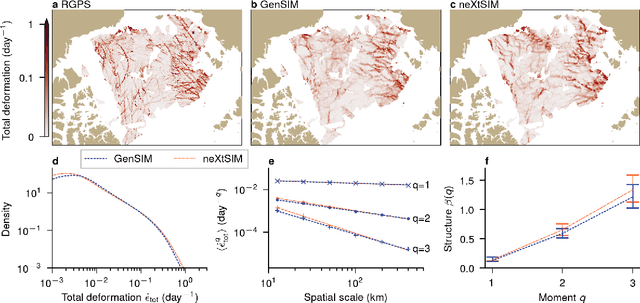
Abstract:Sea ice is governed by highly complex, scale-invariant, and anisotropic processes that are challenging to represent in Earth system models. While advanced numerical models have improved our understanding of the sea-ice dynamics, their computational costs often limit their application in ensemble forecasting and climate simulations. Here, we introduce GenSIM, the first generative AI-based pan-Arctic model that predicts the evolution of all relevant key properties, including concentration, thickness, and drift, in a 12-hour window with improved accuracy over deterministic predictions and high computational efficiency, while remaining physically consistent. Trained on a long simulation from a state-of-the-art sea-ice--ocean system, GenSIM robustly reproduces statistics as observed in numerical models and observations, exhibiting brittle-like short-term dynamics while also depicting the long-term sea-ice decline. Driven solely by atmospheric forcings, we attribute GenSIM's emergent extrapolation capabilities to patterns that reflect the long-term impact of the ocean: it seemingly has learned an internal ocean emulator. This ability to infer slowly evolving climate-relevant dynamics from short-term predictions underlines the large potential of generative models to generalise for unseen climates and to encode hidden physics.
Ensemble Kalman filter in latent space using a variational autoencoder pair
Feb 18, 2025



Abstract:Popular (ensemble) Kalman filter data assimilation (DA) approaches assume that the errors in both the a priori estimate of the state and those in the observations are Gaussian. For constrained variables, e.g. sea ice concentration or stress, such an assumption does not hold. The variational autoencoder (VAE) is a machine learning (ML) technique that allows to map an arbitrary distribution to/from a latent space in which the distribution is supposedly closer to a Gaussian. We propose a novel hybrid DA-ML approach in which VAEs are incorporated in the DA procedure. Specifically, we introduce a variant of the popular ensemble transform Kalman filter (ETKF) in which the analysis is applied in the latent space of a single VAE or a pair of VAEs. In twin experiments with a simple circular model, whereby the circle represents an underlying submanifold to be respected, we find that the use of a VAE ensures that a posteri ensemble members lie close to the manifold containing the truth. Furthermore, online updating of the VAE is necessary and achievable when this manifold varies in time, i.e. when it is non-stationary. We demonstrate that introducing an additional second latent space for the observational innovations improves robustness against detrimental effects of non-Gaussianity and bias in the observational errors but it slightly lessens the performance if observational errors are strictly Gaussian.
Machine learning for modelling unstructured grid data in computational physics: a review
Feb 13, 2025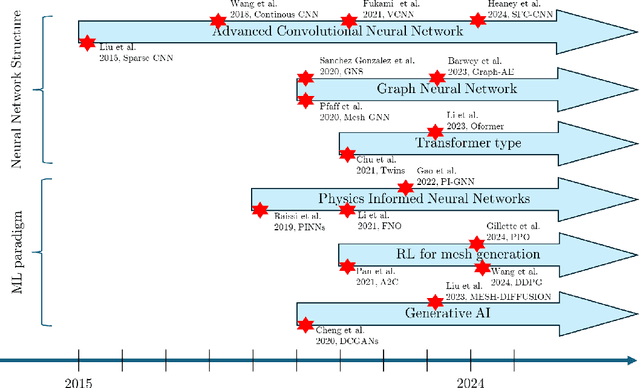
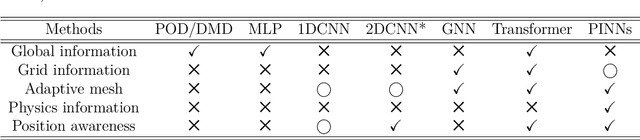
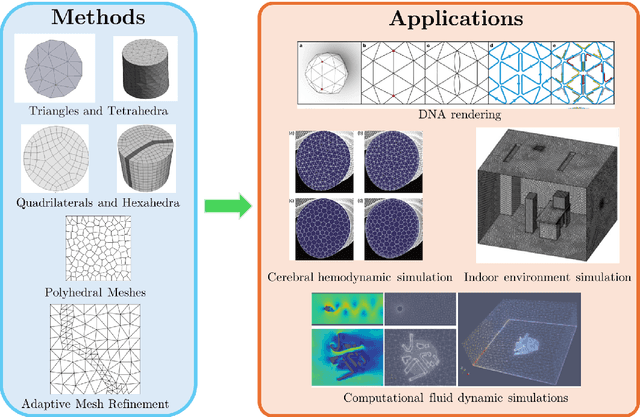

Abstract:Unstructured grid data are essential for modelling complex geometries and dynamics in computational physics. Yet, their inherent irregularity presents significant challenges for conventional machine learning (ML) techniques. This paper provides a comprehensive review of advanced ML methodologies designed to handle unstructured grid data in high-dimensional dynamical systems. Key approaches discussed include graph neural networks, transformer models with spatial attention mechanisms, interpolation-integrated ML methods, and meshless techniques such as physics-informed neural networks. These methodologies have proven effective across diverse fields, including fluid dynamics and environmental simulations. This review is intended as a guidebook for computational scientists seeking to apply ML approaches to unstructured grid data in their domains, as well as for ML researchers looking to address challenges in computational physics. It places special focus on how ML methods can overcome the inherent limitations of traditional numerical techniques and, conversely, how insights from computational physics can inform ML development. To support benchmarking, this review also provides a summary of open-access datasets of unstructured grid data in computational physics. Finally, emerging directions such as generative models with unstructured data, reinforcement learning for mesh generation, and hybrid physics-data-driven paradigms are discussed to inspire future advancements in this evolving field.
Deep learning-based sequential data assimilation for chaotic dynamics identifies local instabilities from single state forecasts
Aug 08, 2024



Abstract:We investigate the ability to discover data assimilation (DA) schemes meant for chaotic dynamics with deep learning (DL). The focus is on learning the analysis step of sequential DA, from state trajectories and their observations, using a simple residual convolutional neural network, while assuming the dynamics to be known. Experiments are performed with the Lorenz 96 dynamics, which display spatiotemporal chaos and for which solid benchmarks for DA performance exist. The accuracy of the states obtained from the learned analysis approaches that of the best possibly tuned ensemble Kalman filter (EnKF), and is far better than that of variational DA alternatives. Critically, this can be achieved while propagating even just a single state in the forecast step. We investigate the reason for achieving ensemble filtering accuracy without an ensemble. We diagnose that the analysis scheme actually identifies key dynamical perturbations, mildly aligned with the unstable subspace, from the forecast state alone, without any ensemble-based covariances representation. This reveals that the analysis scheme has learned some multiplicative ergodic theorem associated to the DA process seen as a non-autonomous random dynamical system.
Towards diffusion models for large-scale sea-ice modelling
Jun 26, 2024



Abstract:We make the first steps towards diffusion models for unconditional generation of multivariate and Arctic-wide sea-ice states. While targeting to reduce the computational costs by diffusion in latent space, latent diffusion models also offer the possibility to integrate physical knowledge into the generation process. We tailor latent diffusion models to sea-ice physics with a censored Gaussian distribution in data space to generate data that follows the physical bounds of the modelled variables. Our latent diffusion models reach similar scores as the diffusion model trained in data space, but they smooth the generated fields as caused by the latent mapping. While enforcing physical bounds cannot reduce the smoothing, it improves the representation of the marginal ice zone. Therefore, for large-scale Earth system modelling, latent diffusion models can have many advantages compared to diffusion in data space if the significant barrier of smoothing can be resolved.
Online model error correction with neural networks: application to the Integrated Forecasting System
Mar 06, 2024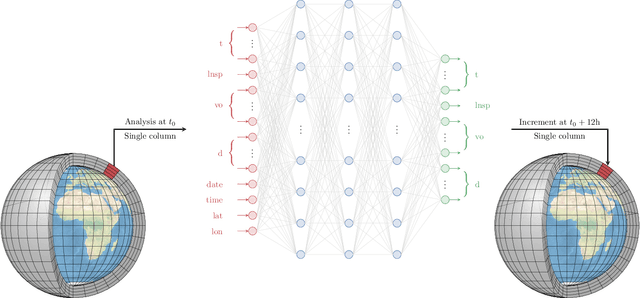
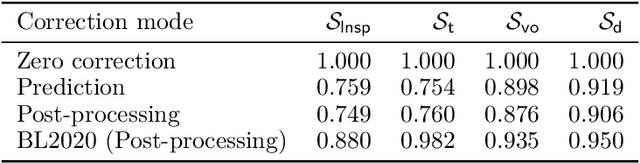
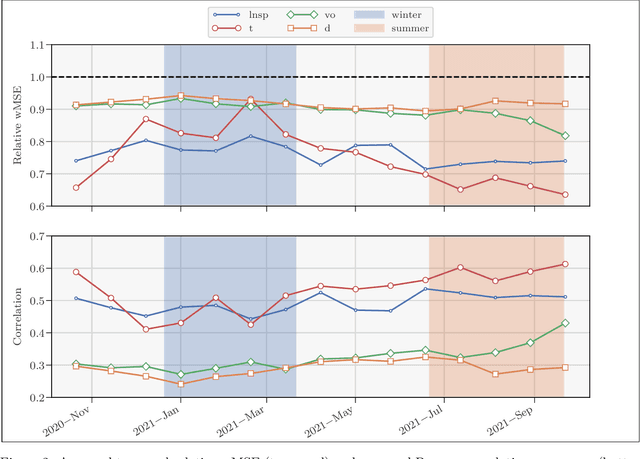
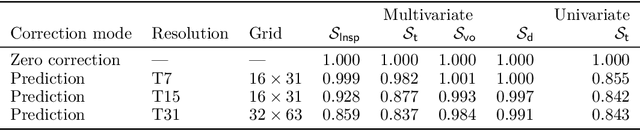
Abstract:In recent years, there has been significant progress in the development of fully data-driven global numerical weather prediction models. These machine learning weather prediction models have their strength, notably accuracy and low computational requirements, but also their weakness: they struggle to represent fundamental dynamical balances, and they are far from being suitable for data assimilation experiments. Hybrid modelling emerges as a promising approach to address these limitations. Hybrid models integrate a physics-based core component with a statistical component, typically a neural network, to enhance prediction capabilities. In this article, we propose to develop a model error correction for the operational Integrated Forecasting System (IFS) of the European Centre for Medium-Range Weather Forecasts using a neural network. The neural network is initially pre-trained offline using a large dataset of operational analyses and analysis increments. Subsequently, the trained network is integrated into the IFS within the Object-Oriented Prediction System (OOPS) so as to be used in data assimilation and forecast experiments. It is then further trained online using a recently developed variant of weak-constraint 4D-Var. The results show that the pre-trained neural network already provides a reliable model error correction, which translates into reduced forecast errors in many conditions and that the online training further improves the accuracy of the hybrid model in many conditions.
Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review
Mar 18, 2023Abstract:Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.
Online model error correction with neural networks in the incremental 4D-Var framework
Oct 25, 2022Abstract:Recent studies have demonstrated that it is possible to combine machine learning with data assimilation to reconstruct the dynamics of a physical model partially and imperfectly observed. Data assimilation is used to estimate the system state from the observations, while machine learning computes a surrogate model of the dynamical system based on those estimated states. The surrogate model can be defined as an hybrid combination where a physical model based on prior knowledge is enhanced with a statistical model estimated by a neural network. The training of the neural network is typically done offline, once a large enough dataset of model state estimates is available. By contrast, with online approaches the surrogate model is improved each time a new system state estimate is computed. Online approaches naturally fit the sequential framework encountered in geosciences where new observations become available with time. In a recent methodology paper, we have developed a new weak-constraint 4D-Var formulation which can be used to train a neural network for online model error correction. In the present article, we develop a simplified version of that method, in the incremental 4D-Var framework adopted by most operational weather centres. The simplified method is implemented in the ECMWF Object-Oriented Prediction System, with the help of a newly developed Fortran neural network library, and tested with a two-layer two-dimensional quasi geostrophic model. The results confirm that online learning is effective and yields a more accurate model error correction than offline learning. Finally, the simplified method is compatible with future applications to state-of-the-art models such as the ECMWF Integrated Forecasting System.
Voltage-Dependent Synaptic Plasticity (VDSP): Unsupervised probabilistic Hebbian plasticity rule based on neurons membrane potential
Apr 14, 2022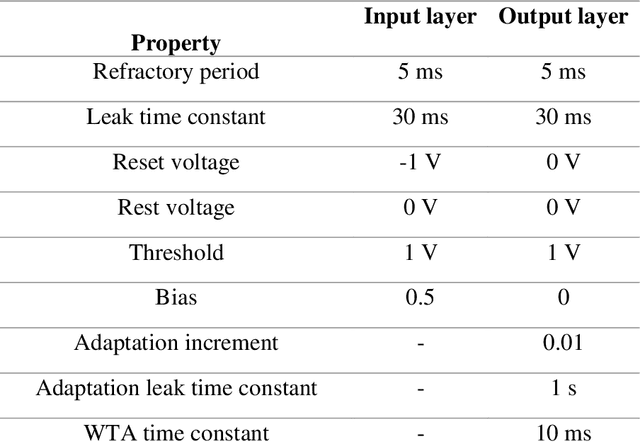
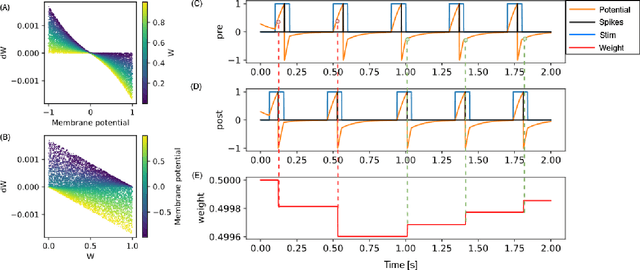
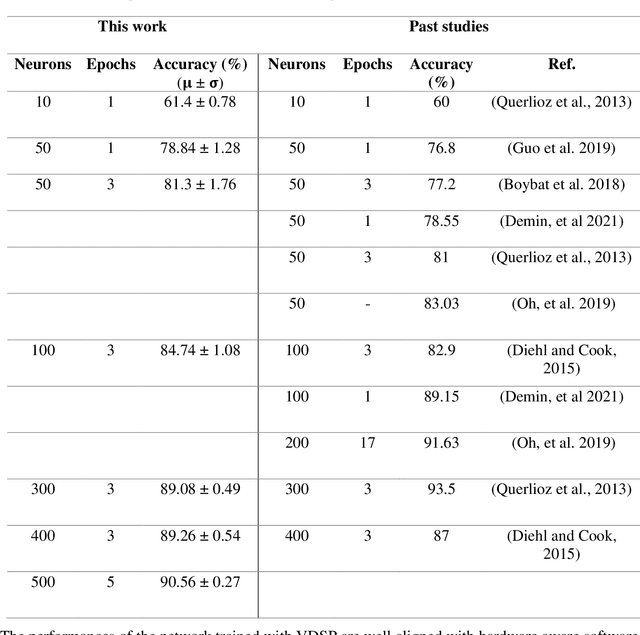
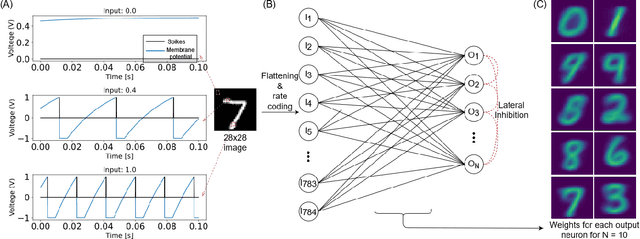
Abstract:This study proposes voltage-dependent-synaptic plasticity (VDSP), a novel brain-inspired unsupervised local learning rule for the online implementation of Hebb's plasticity mechanism on neuromorphic hardware. The proposed VDSP learning rule updates the synaptic conductance on the spike of the postsynaptic neuron only, which reduces by a factor of two the number of updates with respect to standard spike-timing-dependent plasticity (STDP). This update is dependent on the membrane potential of the presynaptic neuron, which is readily available as part of neuron implementation and hence does not require additional memory for storage. Moreover, the update is also regularized on synaptic weight and prevents explosion or vanishing of weights on repeated stimulation. Rigorous mathematical analysis is performed to draw an equivalence between VDSP and STDP. To validate the system-level performance of VDSP, we train a single-layer spiking neural network (SNN) for the recognition of handwritten digits. We report 85.01 $ \pm $ 0.76% (Mean $ \pm $ S.D.) accuracy for a network of 100 output neurons on the MNIST dataset. The performance improves when scaling the network size (89.93 $ \pm $ 0.41% for 400 output neurons, 90.56 $ \pm $ 0.27 for 500 neurons), which validates the applicability of the proposed learning rule for large-scale computer vision tasks. Interestingly, the learning rule better adapts than STDP to the frequency of input signal and does not require hand-tuning of hyperparameters.
State, global and local parameter estimation using local ensemble Kalman filters: applications to online machine learning of chaotic dynamics
Jul 26, 2021
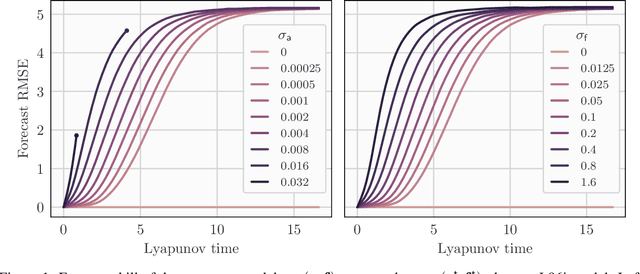

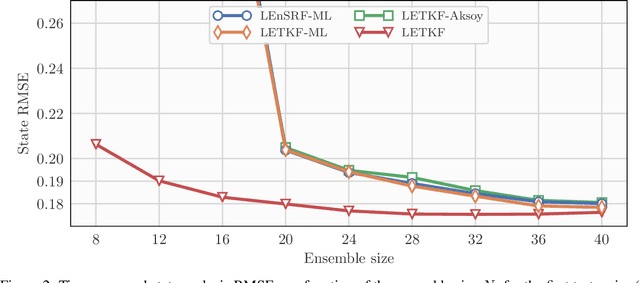
Abstract:In a recent methodological paper, we have shown how to learn chaotic dynamics along with the state trajectory from sequentially acquired observations, using local ensemble Kalman filters. Here, we more systematically investigate the possibilty to use a local ensemble Kalman filter with either covariance localization or local domains, in order to retrieve the state and a mix of key global and local parameters. Global parameters are meant to represent the surrogate dynamics, for instance through a neural network, which is reminiscent of data-driven machine learning of dynamics, while the local parameters typically stand for the forcings of the model. A family of algorithms for covariance and local domain localization is proposed in this joint state and parameter filter context. In particular, we show how to rigorously update global parameters using a local domain EnKF such as the LETKF, an inherently local method. The approach is tested with success on the 40-variable Lorenz model using several of the local EnKF flavors. A two-dimensional illustration based on a multi-layer Lorenz model is finally provided. It uses radiance-like non-local observations, and both local domains and covariance localization in order to learn the chaotic dynamics, the local forcings, and the couplings between layers. This paper more generally addresses the key question of online estimation of both global and local model parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge