State, global and local parameter estimation using local ensemble Kalman filters: applications to online machine learning of chaotic dynamics
Paper and Code
Jul 26, 2021
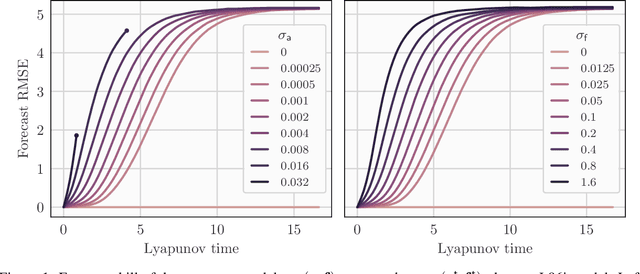

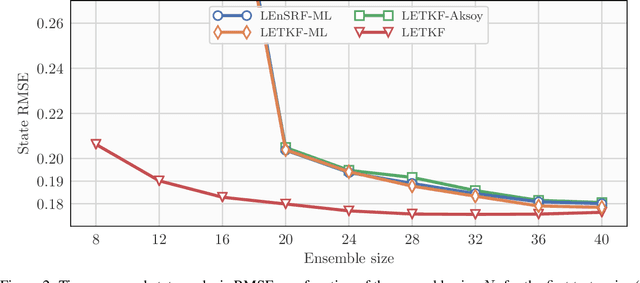
In a recent methodological paper, we have shown how to learn chaotic dynamics along with the state trajectory from sequentially acquired observations, using local ensemble Kalman filters. Here, we more systematically investigate the possibilty to use a local ensemble Kalman filter with either covariance localization or local domains, in order to retrieve the state and a mix of key global and local parameters. Global parameters are meant to represent the surrogate dynamics, for instance through a neural network, which is reminiscent of data-driven machine learning of dynamics, while the local parameters typically stand for the forcings of the model. A family of algorithms for covariance and local domain localization is proposed in this joint state and parameter filter context. In particular, we show how to rigorously update global parameters using a local domain EnKF such as the LETKF, an inherently local method. The approach is tested with success on the 40-variable Lorenz model using several of the local EnKF flavors. A two-dimensional illustration based on a multi-layer Lorenz model is finally provided. It uses radiance-like non-local observations, and both local domains and covariance localization in order to learn the chaotic dynamics, the local forcings, and the couplings between layers. This paper more generally addresses the key question of online estimation of both global and local model parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge