Alberto Carrassi
Generative AI models enable efficient and physically consistent sea-ice simulations
Aug 20, 2025

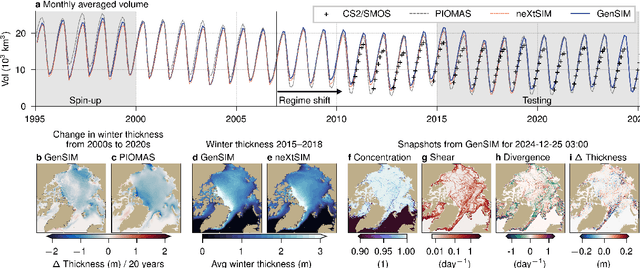
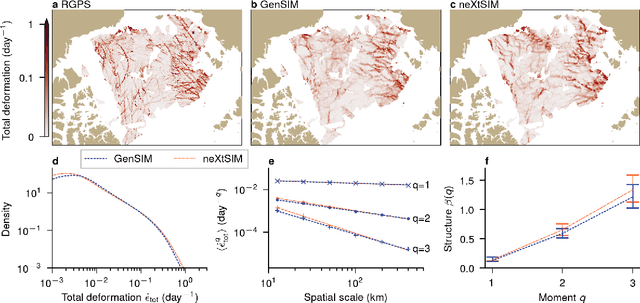
Abstract:Sea ice is governed by highly complex, scale-invariant, and anisotropic processes that are challenging to represent in Earth system models. While advanced numerical models have improved our understanding of the sea-ice dynamics, their computational costs often limit their application in ensemble forecasting and climate simulations. Here, we introduce GenSIM, the first generative AI-based pan-Arctic model that predicts the evolution of all relevant key properties, including concentration, thickness, and drift, in a 12-hour window with improved accuracy over deterministic predictions and high computational efficiency, while remaining physically consistent. Trained on a long simulation from a state-of-the-art sea-ice--ocean system, GenSIM robustly reproduces statistics as observed in numerical models and observations, exhibiting brittle-like short-term dynamics while also depicting the long-term sea-ice decline. Driven solely by atmospheric forcings, we attribute GenSIM's emergent extrapolation capabilities to patterns that reflect the long-term impact of the ocean: it seemingly has learned an internal ocean emulator. This ability to infer slowly evolving climate-relevant dynamics from short-term predictions underlines the large potential of generative models to generalise for unseen climates and to encode hidden physics.
Hybrid machine learning data assimilation for marine biogeochemistry
Apr 07, 2025Abstract:Marine biogeochemistry models are critical for forecasting, as well as estimating ecosystem responses to climate change and human activities. Data assimilation (DA) improves these models by aligning them with real-world observations, but marine biogeochemistry DA faces challenges due to model complexity, strong nonlinearity, and sparse, uncertain observations. Existing DA methods applied to marine biogeochemistry struggle to update unobserved variables effectively, while ensemble-based methods are computationally too expensive for high-complexity marine biogeochemistry models. This study demonstrates how machine learning (ML) can improve marine biogeochemistry DA by learning statistical relationships between observed and unobserved variables. We integrate ML-driven balancing schemes into a 1D prototype of a system used to forecast marine biogeochemistry in the North-West European Shelf seas. ML is applied to predict (i) state-dependent correlations from free-run ensembles and (ii), in an ``end-to-end'' fashion, analysis increments from an Ensemble Kalman Filter. Our results show that ML significantly enhances updates for previously not-updated variables when compared to univariate schemes akin to those used operationally. Furthermore, ML models exhibit moderate transferability to new locations, a crucial step toward scaling these methods to 3D operational systems. We conclude that ML offers a clear pathway to overcome current computational bottlenecks in marine biogeochemistry DA and that refining transferability, optimizing training data sampling, and evaluating scalability for large-scale marine forecasting, should be future research priorities.
Ensemble Kalman filter in latent space using a variational autoencoder pair
Feb 18, 2025



Abstract:Popular (ensemble) Kalman filter data assimilation (DA) approaches assume that the errors in both the a priori estimate of the state and those in the observations are Gaussian. For constrained variables, e.g. sea ice concentration or stress, such an assumption does not hold. The variational autoencoder (VAE) is a machine learning (ML) technique that allows to map an arbitrary distribution to/from a latent space in which the distribution is supposedly closer to a Gaussian. We propose a novel hybrid DA-ML approach in which VAEs are incorporated in the DA procedure. Specifically, we introduce a variant of the popular ensemble transform Kalman filter (ETKF) in which the analysis is applied in the latent space of a single VAE or a pair of VAEs. In twin experiments with a simple circular model, whereby the circle represents an underlying submanifold to be respected, we find that the use of a VAE ensures that a posteri ensemble members lie close to the manifold containing the truth. Furthermore, online updating of the VAE is necessary and achievable when this manifold varies in time, i.e. when it is non-stationary. We demonstrate that introducing an additional second latent space for the observational innovations improves robustness against detrimental effects of non-Gaussianity and bias in the observational errors but it slightly lessens the performance if observational errors are strictly Gaussian.
Deep learning-based sequential data assimilation for chaotic dynamics identifies local instabilities from single state forecasts
Aug 08, 2024



Abstract:We investigate the ability to discover data assimilation (DA) schemes meant for chaotic dynamics with deep learning (DL). The focus is on learning the analysis step of sequential DA, from state trajectories and their observations, using a simple residual convolutional neural network, while assuming the dynamics to be known. Experiments are performed with the Lorenz 96 dynamics, which display spatiotemporal chaos and for which solid benchmarks for DA performance exist. The accuracy of the states obtained from the learned analysis approaches that of the best possibly tuned ensemble Kalman filter (EnKF), and is far better than that of variational DA alternatives. Critically, this can be achieved while propagating even just a single state in the forecast step. We investigate the reason for achieving ensemble filtering accuracy without an ensemble. We diagnose that the analysis scheme actually identifies key dynamical perturbations, mildly aligned with the unstable subspace, from the forecast state alone, without any ensemble-based covariances representation. This reveals that the analysis scheme has learned some multiplicative ergodic theorem associated to the DA process seen as a non-autonomous random dynamical system.
Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review
Mar 18, 2023Abstract:Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.
Combining data assimilation and machine learning to infer unresolved scale parametrisation
Sep 09, 2020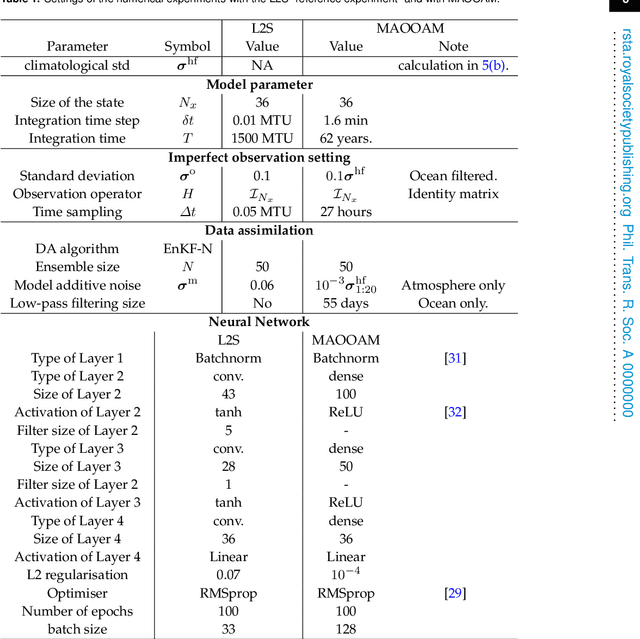
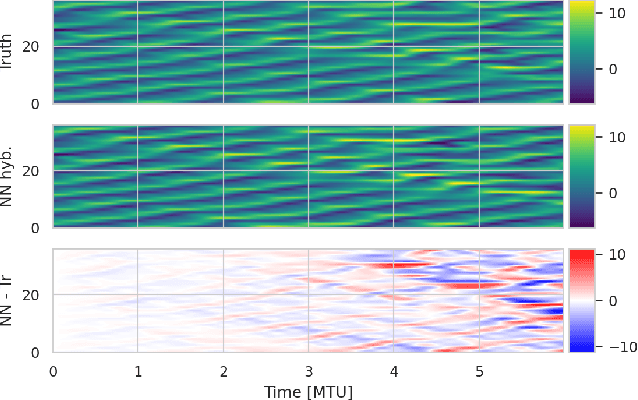
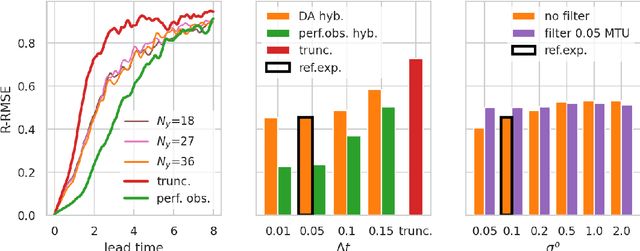
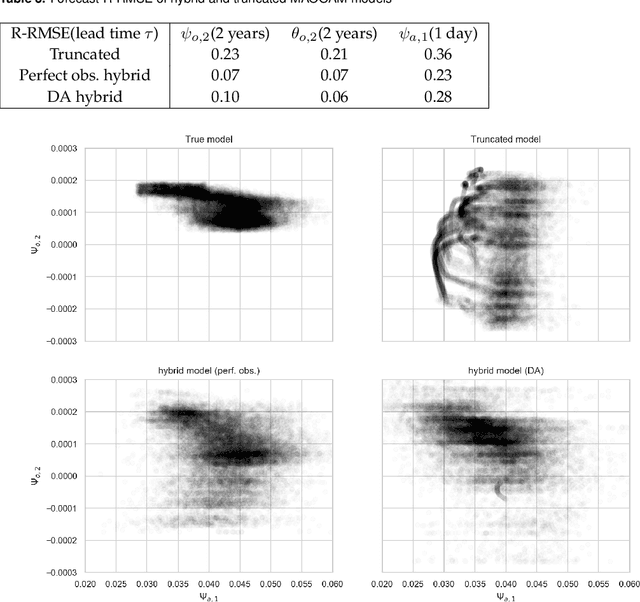
Abstract:In recent years, machine learning (ML) has been proposed to devise data-driven parametrisations of unresolved processes in dynamical numerical models. In most cases, the ML training leverages high-resolution simulations to provide a dense, noiseless target state. Our goal is to go beyond the use of high-resolution simulations and train ML-based parametrisation using direct data, in the realistic scenario of noisy and sparse observations. The algorithm proposed in this work is a two-step process. First, data assimilation (DA) techniques are applied to estimate the full state of the system from a truncated model. The unresolved part of the truncated model is viewed as a model error in the DA system. In a second step, ML is used to emulate the unresolved part, a predictor of model error given the state of the system. Finally, the ML-based parametrisation model is added to the physical core truncated model to produce a hybrid model.
Bayesian inference of dynamics from partial and noisy observations using data assimilation and machine learning
Jan 17, 2020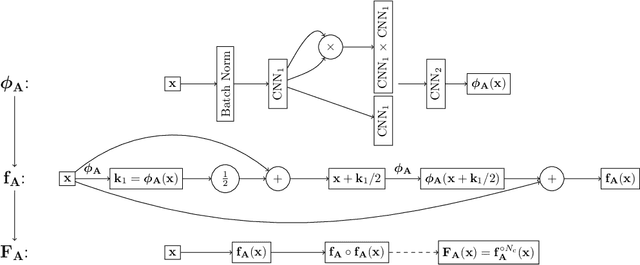
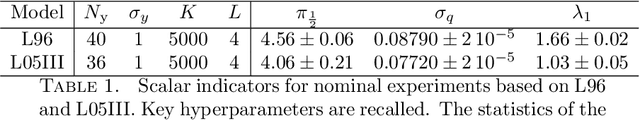
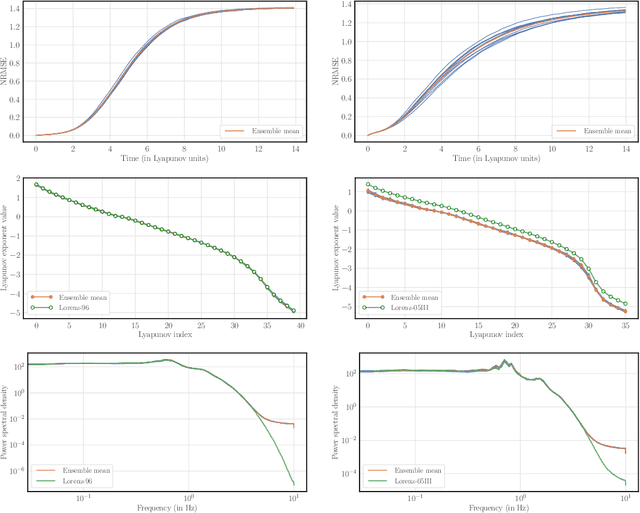
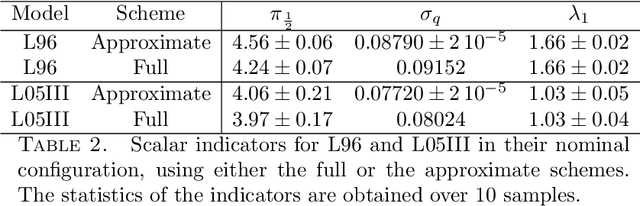
Abstract:The reconstruction from observations of high-dimensional chaotic dynamics such as geophysical flows is hampered by (i) the partial and noisy observations that can realistically be obtained, (ii) the need to learn from long time series of data, and (iii) the unstable nature of the dynamics. To achieve such inference from the observations over long time series, it has been suggested to combine data assimilation and machine learning in several ways. We show how to unify these approaches from a Bayesian perspective using expectation-maximization and coordinate descents. Implementations and approximations of these methods are also discussed. Finally, we numerically and successfully test the approach on two relevant low-order chaotic models with distinct identifiability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge