Super-resolution data assimilation

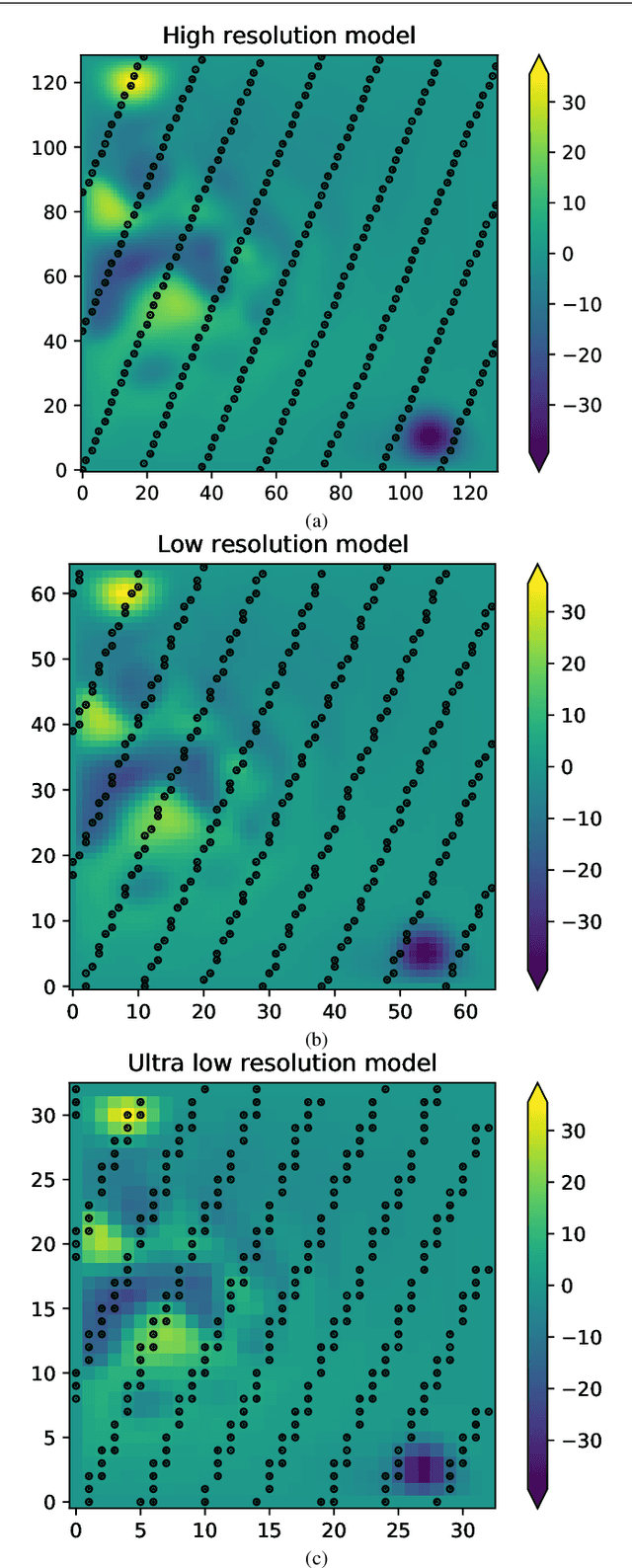
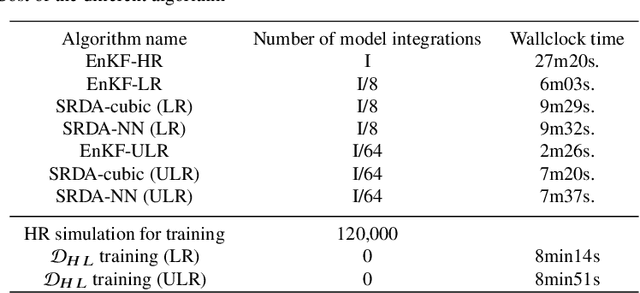
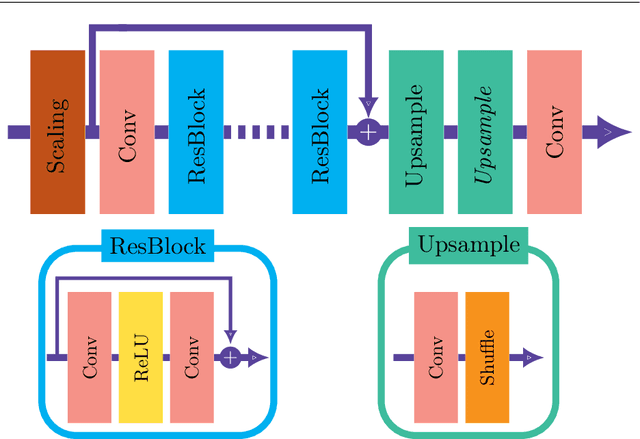
Increasing the resolution of a model can improve the performance of a data assimilation system: first because model field are in better agreement with high resolution observations, then the corrections are better sustained and, with ensemble data assimilation, the forecast error covariances are improved. However, resolution increase is associated with a cubical increase of the computational costs. Here we are testing an approach inspired from images super-resolution techniques and called "Super-resolution data assimilation" (SRDA). Starting from a low-resolution forecast, a neural network (NN) emulates a high-resolution field that is then used to assimilate high-resolution observations. We apply the SRDA to a quasi-geostrophic model representing simplified surface ocean dynamics, with a model resolution up to four times lower than the reference high-resolution and we use the Ensemble Kalman Filter data assimilation method. We show that SRDA outperforms the low-resolution data assimilation approach and a SRDA version with cubic spline interpolation instead of NN. The NN's ability to anticipate the systematic differences between low and high resolution model dynamics explains the enhanced performance, for example by correcting the difference of propagation speed of eddies. Increasing the computational cost by 55\% above the LR data assimilation system (using a 25-members ensemble), the SRDA reduces the errors by 40\% making the performance very close to the HR system (16\% larger, compared to 92\% larger for the LR EnKF). The reliability of the ensemble system is not degraded by SRDA.

Combining data assimilation and machine learning to infer unresolved scale parametrisation

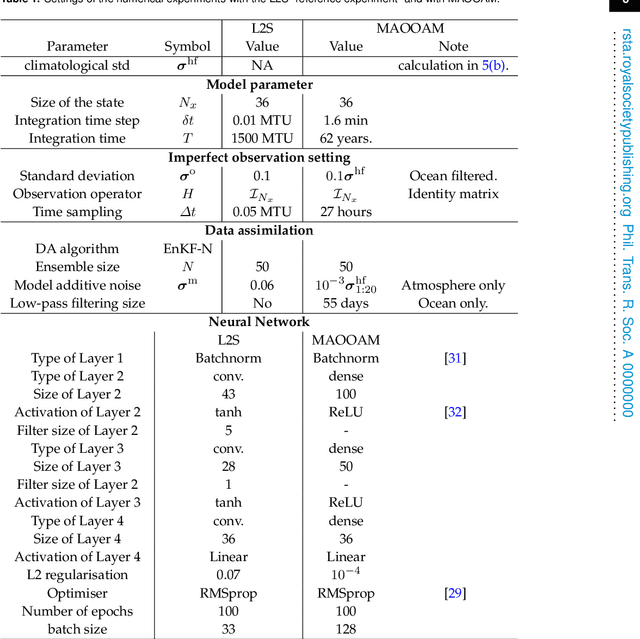
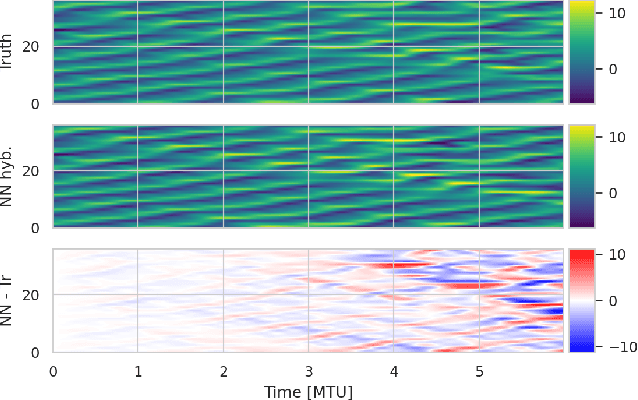
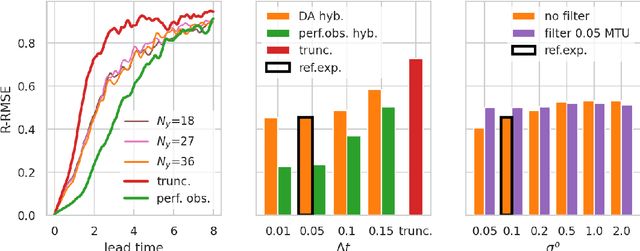
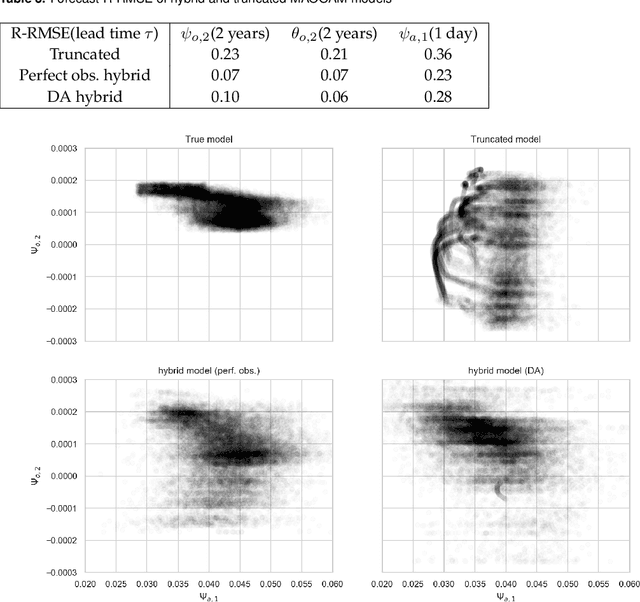
In recent years, machine learning (ML) has been proposed to devise data-driven parametrisations of unresolved processes in dynamical numerical models. In most cases, the ML training leverages high-resolution simulations to provide a dense, noiseless target state. Our goal is to go beyond the use of high-resolution simulations and train ML-based parametrisation using direct data, in the realistic scenario of noisy and sparse observations. The algorithm proposed in this work is a two-step process. First, data assimilation (DA) techniques are applied to estimate the full state of the system from a truncated model. The unresolved part of the truncated model is viewed as a model error in the DA system. In a second step, ML is used to emulate the unresolved part, a predictor of model error given the state of the system. Finally, the ML-based parametrisation model is added to the physical core truncated model to produce a hybrid model.

Bayesian inference of dynamics from partial and noisy observations using data assimilation and machine learning

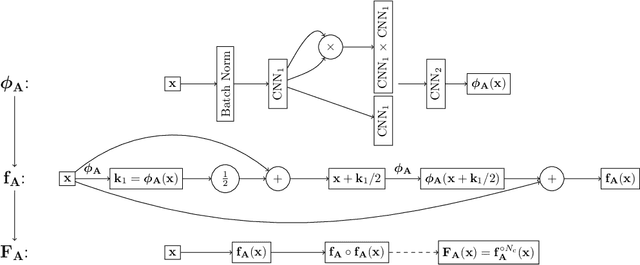
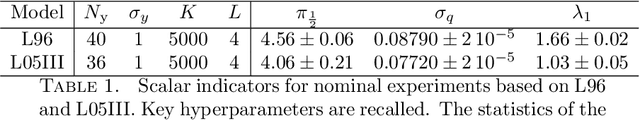
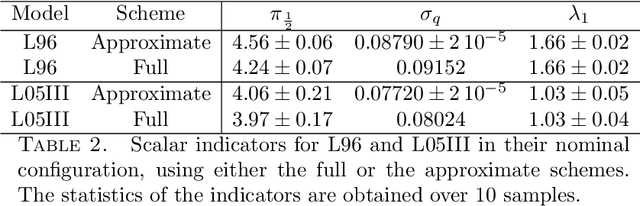
The reconstruction from observations of high-dimensional chaotic dynamics such as geophysical flows is hampered by (i) the partial and noisy observations that can realistically be obtained, (ii) the need to learn from long time series of data, and (iii) the unstable nature of the dynamics. To achieve such inference from the observations over long time series, it has been suggested to combine data assimilation and machine learning in several ways. We show how to unify these approaches from a Bayesian perspective using expectation-maximization and coordinate descents. Implementations and approximations of these methods are also discussed. Finally, we numerically and successfully test the approach on two relevant low-order chaotic models with distinct identifiability.

Combining data assimilation and machine learning to emulate a dynamical model from sparse and noisy observations: a case study with the Lorenz 96 model

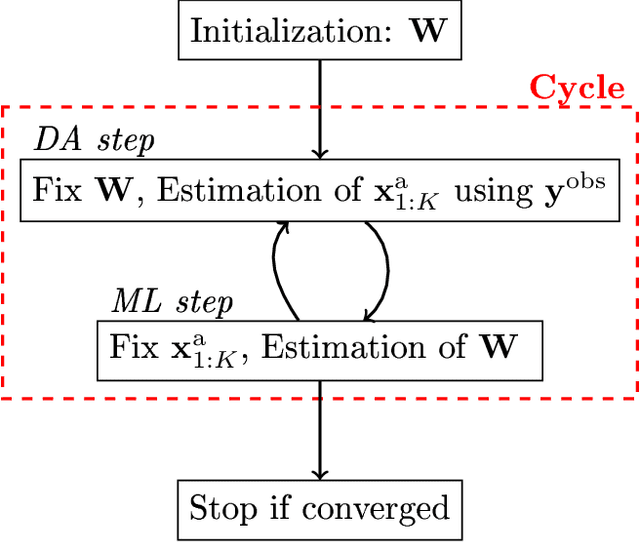
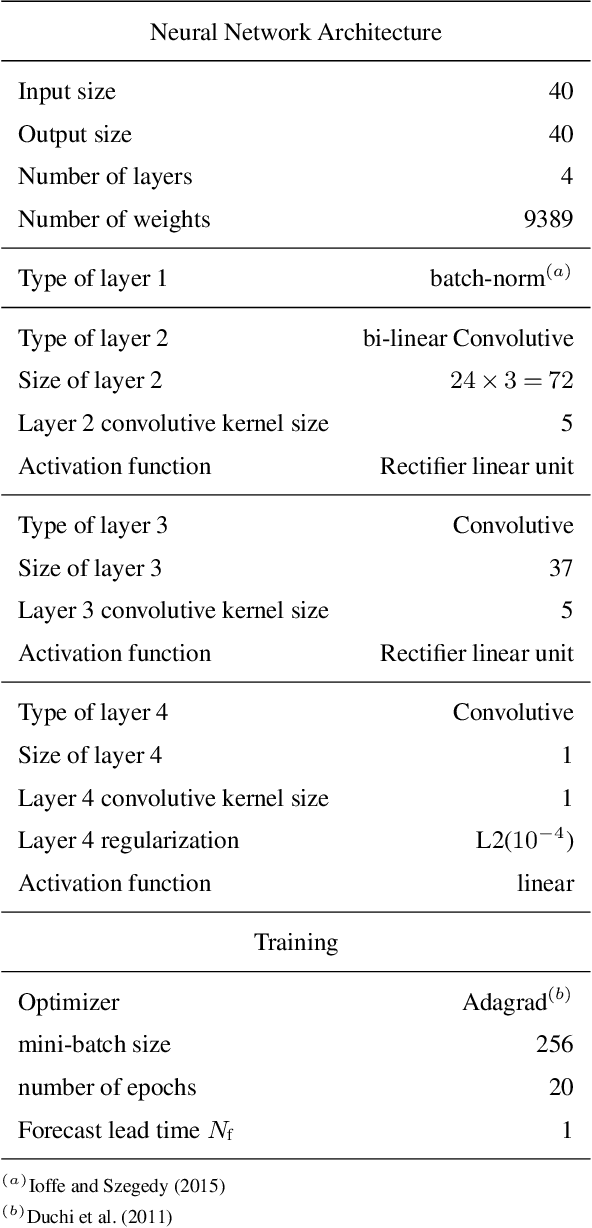
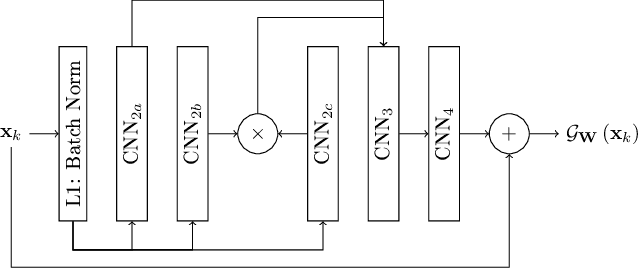
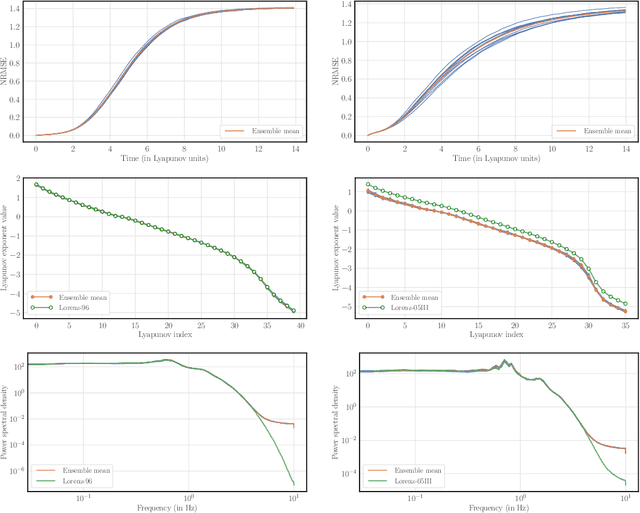
A novel method, based on the combination of data assimilation and machine learning is introduced. The new hybrid approach is designed for a two-fold scope: (i) emulating hidden, possibly chaotic, dynamics and (ii) predicting their future states. The method consists in applying iteratively a data assimilation step, here an ensemble Kalman filter, and a neural network. Data assimilation is used to optimally combine a surrogate model with sparse noisy data. The output analysis is spatially complete and is used as a training set by the neural network to update the surrogate model. The two steps are then repeated iteratively. Numerical experiments have been carried out using the chaotic 40-variables Lorenz 96 model, proving both convergence and statistical skills of the proposed hybrid approach. The surrogate model shows short-term forecast skills up to two Lyapunov times, the retrieval of positive Lyapunov exponents as well as the more energetic frequencies of the power density spectrum. The sensitivity of the method to critical setup parameters is also presented: forecast skills decrease smoothly with increased observational noise but drops abruptly if less than half of the model domain is observed. The successful synergy between data assimilation and machine learning, proven here with a low-dimensional system, encourages further investigation of such hybrids with more sophisticated dynamics.