Online model error correction with neural networks in the incremental 4D-Var framework

Recent studies have demonstrated that it is possible to combine machine learning with data assimilation to reconstruct the dynamics of a physical model partially and imperfectly observed. Data assimilation is used to estimate the system state from the observations, while machine learning computes a surrogate model of the dynamical system based on those estimated states. The surrogate model can be defined as an hybrid combination where a physical model based on prior knowledge is enhanced with a statistical model estimated by a neural network. The training of the neural network is typically done offline, once a large enough dataset of model state estimates is available. By contrast, with online approaches the surrogate model is improved each time a new system state estimate is computed. Online approaches naturally fit the sequential framework encountered in geosciences where new observations become available with time. In a recent methodology paper, we have developed a new weak-constraint 4D-Var formulation which can be used to train a neural network for online model error correction. In the present article, we develop a simplified version of that method, in the incremental 4D-Var framework adopted by most operational weather centres. The simplified method is implemented in the ECMWF Object-Oriented Prediction System, with the help of a newly developed Fortran neural network library, and tested with a two-layer two-dimensional quasi geostrophic model. The results confirm that online learning is effective and yields a more accurate model error correction than offline learning. Finally, the simplified method is compatible with future applications to state-of-the-art models such as the ECMWF Integrated Forecasting System.

A comparison of combined data assimilation and machine learning methods for offline and online model error correction

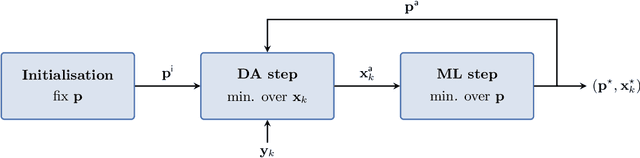
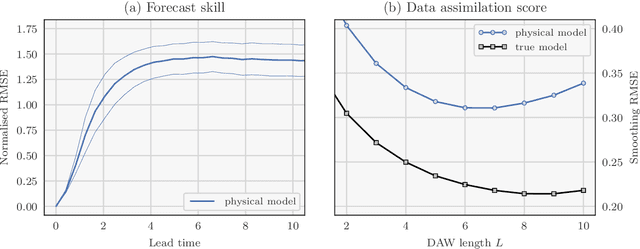
Recent studies have shown that it is possible to combine machine learning methods with data assimilation to reconstruct a dynamical system using only sparse and noisy observations of that system. The same approach can be used to correct the error of a knowledge-based model. The resulting surrogate model is hybrid, with a statistical part supplementing a physical part. In practice, the correction can be added as an integrated term (i.e. in the model resolvent) or directly inside the tendencies of the physical model. The resolvent correction is easy to implement. The tendency correction is more technical, in particular it requires the adjoint of the physical model, but also more flexible. We use the two-scale Lorenz model to compare the two methods. The accuracy in long-range forecast experiments is somewhat similar between the surrogate models using the resolvent correction and the tendency correction. By contrast, the surrogate models using the tendency correction significantly outperform the surrogate models using the resolvent correction in data assimilation experiments. Finally, we show that the tendency correction opens the possibility to make online model error correction, i.e. improving the model progressively as new observations become available. The resulting algorithm can be seen as a new formulation of weak-constraint 4D-Var. We compare online and offline learning using the same framework with the two-scale Lorenz system, and show that with online learning, it is possible to extract all the information from sparse and noisy observations.

Using machine learning to correct model error in data assimilation and forecast applications

The idea of using machine learning (ML) methods to reconstruct the dynamics of a system is the topic of recent studies in the geosciences, in which the key output is a surrogate model meant to emulate the dynamical model. In order to treat sparse and noisy observations in a rigorous way, ML can be combined to data assimilation (DA). This yields a class of iterative methods in which, at each iteration a DA step assimilates the observations, and alternates with a ML step to learn the underlying dynamics of the DA analysis. In this article, we propose to use this method to correct the error of an existent, knowledge-based model. In practice, the resulting surrogate model is an hybrid model between the original (knowledge-based) model and the ML model. We demonstrate numerically the feasibility of the method using a two-layer, two-dimensional quasi-geostrophic channel model. Model error is introduced by the means of perturbed parameters. The DA step is performed using the strong-constraint 4D-Var algorithm, while the ML step is performed using deep learning tools. The ML models are able to learn a substantial part of the model error and the resulting hybrid surrogate models produce better short- to mid-range forecasts. Furthermore, using the hybrid surrogate models for DA yields a significantly better analysis than using the original model.