EM-like Learning Chaotic Dynamics from Noisy and Partial Observations
Paper and Code
Mar 25, 2019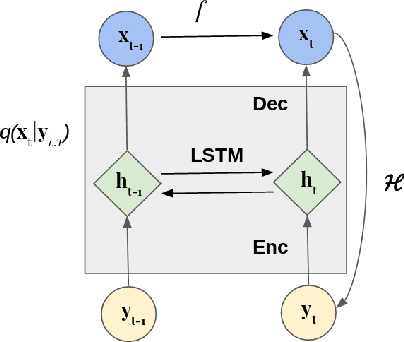
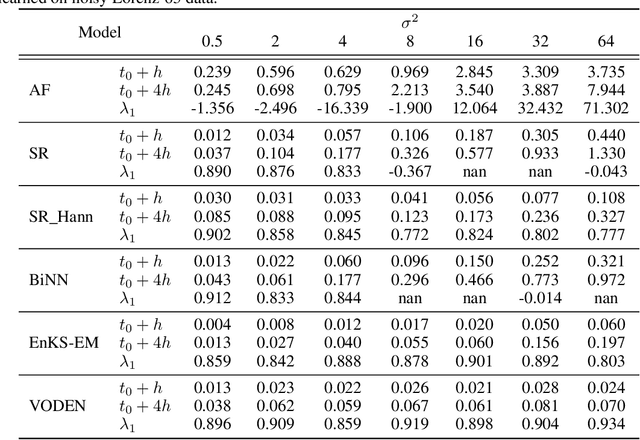
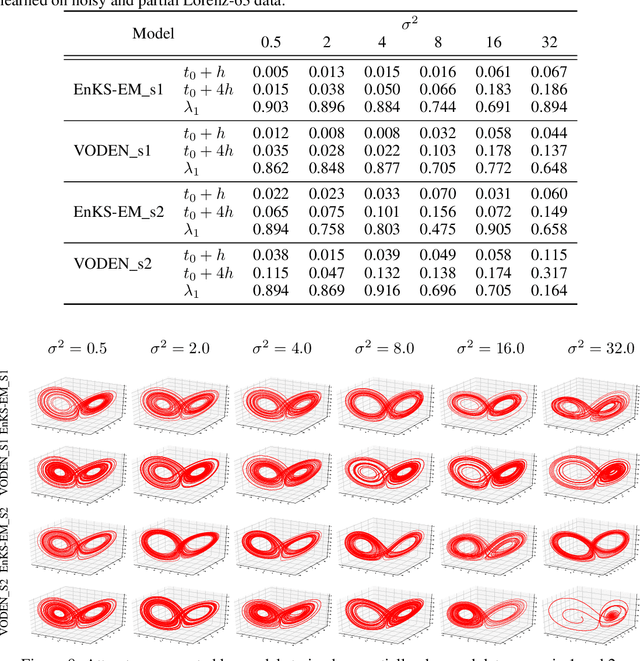
The identification of the governing equations of chaotic dynamical systems from data has recently emerged as a hot topic. While the seminal work by Brunton et al. reported proof-of-concepts for idealized observation setting for fully-observed systems, {\em i.e.} large signal-to-noise ratios and high-frequency sampling of all system variables, we here address the learning of data-driven representations of chaotic dynamics for partially-observed systems, including significant noise patterns and possibly lower and irregular sampling setting. Instead of considering training losses based on short-term prediction error like state-of-the-art learning-based schemes, we adopt a Bayesian formulation and state this issue as a data assimilation problem with unknown model parameters. To solve for the joint inference of the hidden dynamics and of model parameters, we combine neural-network representations and state-of-the-art assimilation schemes. Using iterative Expectation-Maximization (EM)-like procedures, the key feature of the proposed inference schemes is the derivation of the posterior of the hidden dynamics. Using a neural-network-based Ordinary Differential Equation (ODE) representation of these dynamics, we investigate two strategies: their combination to Ensemble Kalman Smoothers and Long Short-Term Memory (LSTM)-based variational approximations of the posterior. Through numerical experiments on the Lorenz-63 system with different noise and time sampling settings, we demonstrate the ability of the proposed schemes to recover and reproduce the hidden chaotic dynamics, including their Lyapunov characteristic exponents, when classic machine learning approaches fail.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge