Laurent Debreu
Learning Runge-Kutta Integration Schemes for ODE Simulation and Identification
May 11, 2021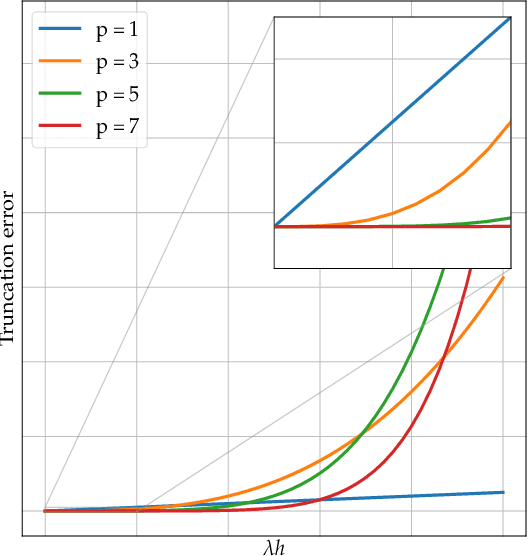

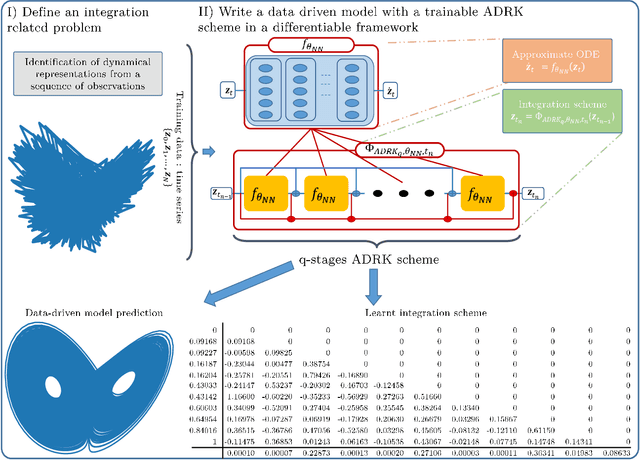
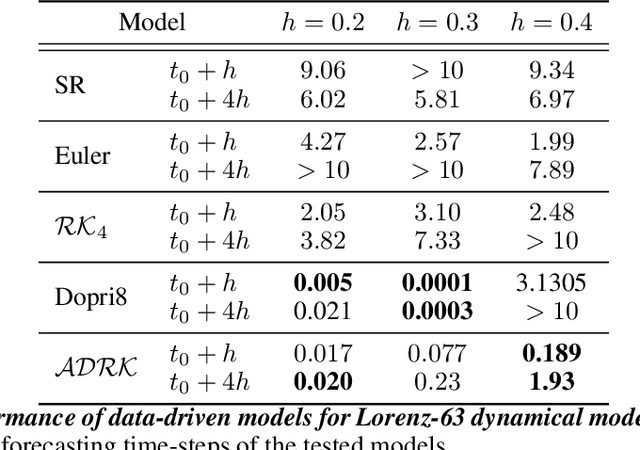
Abstract:Deriving analytical solutions of ordinary differential equations is usually restricted to a small subset of problems and numerical techniques are considered. Inevitably, a numerical simulation of a differential equation will then always be distinct from a true analytical solution. An efficient integration scheme shall further not only provide a trajectory throughout a given state, but also be derived to ensure the generated simulation to be close to the analytical one. Consequently, several integration schemes were developed for different classes of differential equations. Unfortunately, when considering the integration of complex non-linear systems, as well as the identification of non-linear equations from data, this choice of the integration scheme is often far from being trivial. In this paper, we propose a novel framework to learn integration schemes that minimize an integration-related cost function. We demonstrate the relevance of the proposed learning-based approach for non-linear equations and include a quantitative analysis w.r.t. classical state-of-the-art integration techniques, especially where the latter may not apply.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge