Stochastic full waveform inversion with deep generative prior for uncertainty quantification

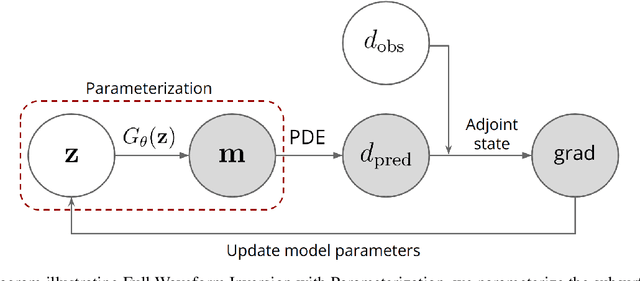
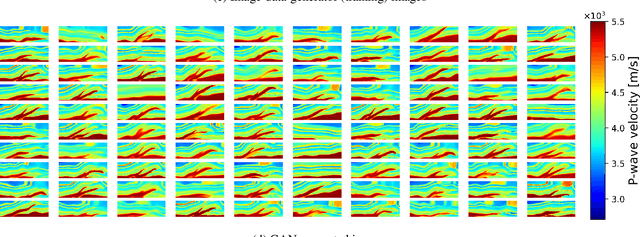
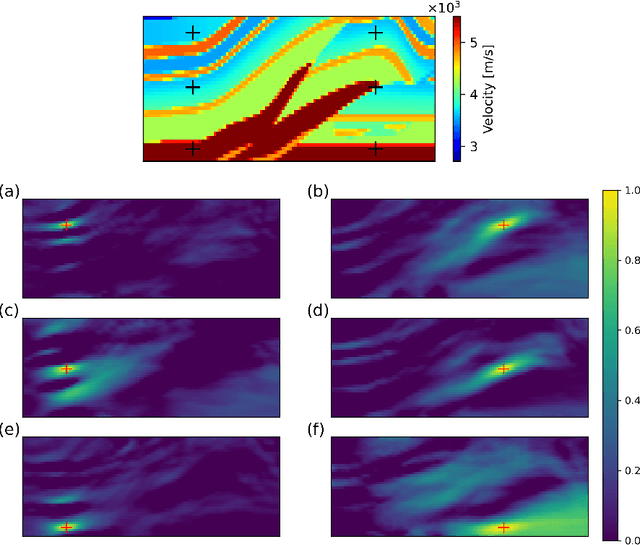
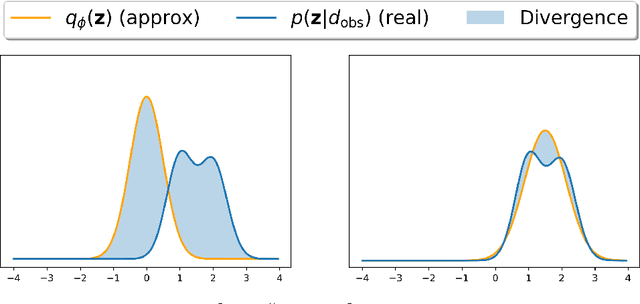
To obtain high-resolution images of subsurface structures from seismic data, seismic imaging techniques such as Full Waveform Inversion (FWI) serve as crucial tools. However, FWI involves solving a nonlinear and often non-unique inverse problem, presenting challenges such as local minima trapping and inadequate handling of inherent uncertainties. In addressing these challenges, we propose leveraging deep generative models as the prior distribution of geophysical parameters for stochastic Bayesian inversion. This approach integrates the adjoint state gradient for efficient back-propagation from the numerical solution of partial differential equations. Additionally, we introduce explicit and implicit variational Bayesian inference methods. The explicit method computes variational distribution density using a normalizing flow-based neural network, enabling computation of the Bayesian posterior of parameters. Conversely, the implicit method employs an inference network attached to a pretrained generative model to estimate density, incorporating an entropy estimator. Furthermore, we also experimented with the Stein Variational Gradient Descent (SVGD) method as another variational inference technique, using particles. We compare these variational Bayesian inference methods with conventional Markov chain Monte Carlo (McMC) sampling. Each method is able to quantify uncertainties and to generate seismic data-conditioned realizations of subsurface geophysical parameters. This framework provides insights into subsurface structures while accounting for inherent uncertainties.

SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

A principled deep learning approach for geological facies generation

The simulation of geological facies in an unobservable volume is essential in various geoscience applications. Given the complexity of the problem, deep generative learning is a promising approach to overcome the limitations of traditional geostatistical simulation models, in particular their lack of physical realism. This research aims to investigate the application of generative adversarial networks and deep variational inference for conditionally simulating meandering channels in underground volumes. In this paper, we review the generative deep learning approaches, in particular the adversarial ones and the stabilization techniques that aim to facilitate their training. The proposed approach is tested on 2D and 3D simulations generated by the stochastic process-based model Flumy. Morphological metrics are utilized to compare our proposed method with earlier iterations of generative adversarial networks. The results indicate that by utilizing recent stabilization techniques, generative adversarial networks can efficiently sample from target data distributions. Moreover, we demonstrate the ability to simulate conditioned simulations through the latent variable model property of the proposed approach.